変分自己符号化器 (VAE) の学習によるイメージ生成

R2026b

この例では、深層学習変分自己符号化器 (VAE) に学習させ、イメージを生成する方法を説明します。

データの集合内の観測値を強く表すデータを生成するために、変分自己符号化器を使用できます。自己符号化器は、入力を低次元空間に変換 (符号化ステップ) し、低次元表現から入力を再構成 (復号化ステップ) することによって、入力を複製するように学習させるモデルの一種です。

この図は、数字のイメージを再構成する自己符号化器の基本構造を示しています。

変分自己符号化器を使用して新しいイメージを生成するには、ランダムベクトルを復号化器に入力します。

"変分" 自己符号化器は、潜在空間に確率分布を適用してその分布を学習することで、復号化器からの出力の分布と観測データの分布を一致させるという点で、通常の自己符号化器と異なります。特に、潜在出力は、符号化器が学習した分布からランダムにサンプリングされます。

データの読み込み

関数 digitTrain4DArrayData と digitTest4DArrayData を使用して、インメモリ数値配列として数字データを読み込みます。数字データセットは、10,000 個の手書き数字の合成グレースケールイメージで構成されています。各イメージは 28×28 ピクセルです。

XTrain = digitTrain4DArrayData;
XTest = digitTest4DArrayData;

ネットワークアーキテクチャの定義

自己符号化器には、符号化器と復号化器の 2 つの部分があります。符号化器は、イメージ入力を受け取り、畳み込みなどの一連のダウンサンプリング演算を使用して潜在ベクトル表現を出力 (符号化) します。同様に、復号化器は潜在ベクトル表現を入力として受け取り、転置畳み込みなどの一連のアップサンプリング演算を使用して入力を再構成します。

入力をサンプリングするために、この例ではカスタム層 samplingLayer を使用します。この層にアクセスするには、この例をライブスクリプトとして開きます。層は、対数分散ベクトル $log (σ^{2})$ と連結された平均ベクトル $μ$ を入力として受け取り、 $N (μ_{i}, σ_{i}^{2})$ から要素をサンプリングします。層は対数分散を使用して、学習プロセスをより数値的に安定させます。

符号化器ネットワークアーキテクチャの定義

28×28×1 のイメージを 32 行 1 列の潜在ベクトルにダウンサンプリングする次の符号化器ネットワークを定義します。

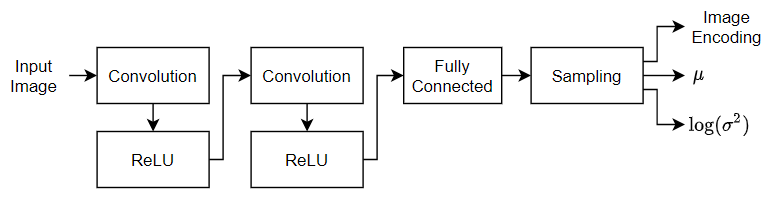
イメージ入力用に、学習データと一致する入力サイズのイメージ入力層を指定します。データは正規化しません。
入力をダウンサンプリングするために、2 次元畳み込み層と ReLU 層のブロックを 2 つ指定します。
平均と対数分散の連結ベクトルを出力するために、潜在チャネル数の 2 倍の出力チャネル数をもつ全結合層を指定します。
統計で指定された符号化をサンプリングするために、カスタム層 samplingLayer を使用してサンプリング層を含めます。この層にアクセスするには、この例をライブスクリプトとして開きます。

numLatentChannels = 32;
imageSize = [28 28 1];

layersE = [
    imageInputLayer(imageSize,Normalization="none")
    convolution2dLayer(3,32,Padding="same",Stride=2)
    reluLayer
    convolution2dLayer(3,64,Padding="same",Stride=2)
    reluLayer
    fullyConnectedLayer(2*numLatentChannels)
    samplingLayer];

復号化器ネットワークアーキテクチャの定義

32 行 1 列の潜在ベクトルから 28×28×1 のイメージを再構成する次の復号化器ネットワークを定義します。

特徴ベクトル入力用に、潜在チャネルの数と一致する入力サイズをもつ特徴入力層を指定します。
この例にサポートファイルとして添付されているカスタム層 projectAndReshapeLayer を使用し、潜在入力を 7×7×64 の配列に投影して形状変更します。この層にアクセスするには、この例をライブスクリプトとして開きます。[7 7 64] の投影サイズを指定します。
入力をアップサンプリングするために、転置畳み込み層と ReLU 層のブロックを 2 つ指定します。
28×28×1 のサイズのイメージを出力するために、3 行 3 列のフィルターを 1 つもつ転置畳み込み層を含めます。
出力を [0,1] の範囲の値にマッピングするために、シグモイド活性化層を含めます。

projectionSize = [7 7 64];
numInputChannels = imageSize(3);

layersD = [
    featureInputLayer(numLatentChannels)
    projectAndReshapeLayer(projectionSize)
    transposedConv2dLayer(3,64,Cropping="same",Stride=2)
    reluLayer
    transposedConv2dLayer(3,32,Cropping="same",Stride=2)
    reluLayer
    transposedConv2dLayer(3,numInputChannels,Cropping="same")
    sigmoidLayer];

カスタム学習ループを使用して両方のネットワークに学習させ、自動微分を有効にするために、層配列を dlnetwork オブジェクトに変換します。

netE = dlnetwork(layersE);
netD = dlnetwork(layersD);

モデル損失関数の定義

モデルの損失と、学習可能なパラメーターについての損失の勾配を返す関数を定義します。

例においてモデル損失関数の節で定義されている関数 modelLoss は、符号化器ネットワークと復号化器ネットワーク、および入力データのミニバッチを入力として受け取り、ネットワーク内の学習可能なパラメーターの損失と損失の勾配を返します。損失を計算するために、この関数は、例において ELBO 損失関数の節で定義されている関数 ELBOloss を使用し、符号化器によって出力された平均と対数分散を入力として受け取り、それらを使用して証拠下限 (ELBO) 損失を計算します。

学習オプションの指定

ミニバッチサイズを 128、学習率を 0.001 として、150 エポック学習させます。

numEpochs = 150;
miniBatchSize = 128;
learnRate = 1e-3;

モデルの学習

カスタム学習ループを使用してモデルに学習させます。

学習中にイメージのミニバッチを処理および管理するminibatchqueueオブジェクトを作成します。各ミニバッチで次を行います。

学習データを配列データストアに変換します。4 番目の次元で反復するように指定します。
カスタムミニバッチ前処理関数 preprocessMiniBatch (この例の最後で定義) を使用し、複数の観測値を単一のミニバッチに連結します。
イメージデータを次元ラベル "SSCB" (spatial、spatial、channel、batch) で形式を整えます。既定では、minibatchqueue オブジェクトは、基となる型が single の dlarray オブジェクトにデータを変換します。
GPU が利用できる場合、GPU で学習を行います。既定では、minibatchqueue オブジェクトは、GPU が利用可能な場合、各出力を gpuArray に変換します。GPU を使用するには、Parallel Computing Toolbox™ とサポートされている GPU デバイスが必要です。サポートされているデバイスの詳細については、GPU 計算の要件 (Parallel Computing Toolbox)を参照してください。
すべてのミニバッチが確実に同じサイズになるように、部分的なミニバッチをすべて破棄します。

dsTrain = arrayDatastore(XTrain,IterationDimension=4);
numOutputs = 1;

mbq = minibatchqueue(dsTrain,numOutputs, ...
    MiniBatchSize = miniBatchSize, ...
    MiniBatchFcn=@preprocessMiniBatch, ...
    MiniBatchFormat="SSCB", ...
    PartialMiniBatch="discard");

Adam ソルバーのパラメーターを初期化します。

trailingAvgE = [];
trailingAvgSqE = [];
trailingAvgD = [];
trailingAvgSqD = [];

学習の進行状況モニター用に合計反復回数を計算します。

numObservationsTrain = size(XTrain,4);
numIterationsPerEpoch = floor(numObservationsTrain / miniBatchSize);
numIterations = numEpochs * numIterationsPerEpoch;

学習の進行状況モニターを初期化します。監視オブジェクトを作成するとタイマーが開始されるため、学習ループに近いところでオブジェクトを作成するようにしてください。

monitor = trainingProgressMonitor( ...
Metrics="Loss", ...
Info="Epoch", ...
XLabel="Iteration");

カスタム学習ループを使用してネットワークに学習させます。各エポックについて、データをシャッフルしてデータのミニバッチをループで回します。各ミニバッチで次を行います。

関数 dlfeval および modelLoss を使用してモデルの損失と勾配を評価します。
関数 adamupdate を使用して符号化器および復号化器のネットワークパラメーターを更新します。
学習の進行状況を表示します。

epoch = 0;
iteration = 0;

% Loop over epochs.
while epoch < numEpochs && ~monitor.Stop
    epoch = epoch + 1;

    % Shuffle data.
    shuffle(mbq);

    % Loop over mini-batches.
    while hasdata(mbq) && ~monitor.Stop
        iteration = iteration + 1;

        % Read mini-batch of data.
        X = next(mbq);

        % Evaluate loss and gradients.
        [loss,gradientsE,gradientsD] = dlfeval(@modelLoss,netE,netD,X);

        % Update learnable parameters.
        [netE,trailingAvgE,trailingAvgSqE] = adamupdate(netE, ...
            gradientsE,trailingAvgE,trailingAvgSqE,iteration,learnRate);

        [netD, trailingAvgD, trailingAvgSqD] = adamupdate(netD, ...
            gradientsD,trailingAvgD,trailingAvgSqD,iteration,learnRate);

        % Update the training progress monitor. 
        recordMetrics(monitor,iteration,Loss=loss);
        updateInfo(monitor,Epoch=epoch + " of " + numEpochs);
        monitor.Progress = 100*iteration/numIterations;
    end
end

ネットワークのテスト

学習済みの自己符号化器を、ホールドアウトされたテストセットでテストします。学習データの場合と同じ手順を使用して、データのミニバッチキューを作成します。ただし、データの部分的なミニバッチは破棄しません。

dsTest = arrayDatastore(XTest,IterationDimension=4);
numOutputs = 1;

mbqTest = minibatchqueue(dsTest,numOutputs, ...
    MiniBatchSize = miniBatchSize, ...
    MiniBatchFcn=@preprocessMiniBatch, ...
    MiniBatchFormat="SSCB");

関数 modelPredictions を使用し、学習済みの自己符号化器を使用して予測を行います。

YTest = modelPredictions(netE,netD,mbqTest);

テストイメージと再構成後のイメージの平均二乗誤差を取得し、それらをヒストグラムで可視化することで、再構成誤差を可視化します。

err = mean((XTest-YTest).^2,[1 2 3]);
figure
histogram(err)
xlabel("Error")
ylabel("Frequency")
title("Test Data")

Figure contains an axes object. The axes object with title Test Data, xlabel Error, ylabel Frequency contains an object of type histogram.

新しいイメージの生成

ランダムにサンプリングされたイメージ符号化を復号化器に渡して、新しいイメージのバッチを生成します。

numImages = 64;

ZNew = randn(numLatentChannels,numImages);
ZNew = dlarray(ZNew,"CB");

YNew = predict(netD,ZNew);
YNew = extractdata(YNew);

生成されたイメージを Figure に表示します。

figure
I = imtile(YNew);
imshow(I)
title("Generated Images")

Figure contains an axes object. The hidden axes object with title Generated Images contains an object of type image.

ここでは、学習データと同様のイメージを生成できるように、VAE に強い特徴表現を学習させました。

補助関数

モデル損失関数

関数 modelLoss は、符号化器ネットワークと復号化器ネットワーク、および入力データのミニバッチを入力として受け取り、ネットワーク内の学習可能なパラメーターの損失と損失の勾配を返します。この関数は、学習イメージを符号化器に渡し、結果のイメージ符号化を復号化器に渡します。損失を計算するために、この関数は、符号化器のサンプリング層によって出力された平均および対数分散統計を使って関数 elboLoss を使用します。

function [loss,gradientsE,gradientsD] = modelLoss(netE,netD,X)

% Forward through encoder.
[Z,mu,logSigmaSq] = forward(netE,X);

% Forward through decoder.
Y = forward(netD,Z);

% Calculate loss and gradients.
loss = elboLoss(Y,X,mu,logSigmaSq);
[gradientsE,gradientsD] = dlgradient(loss,netE.Learnables,netD.Learnables);

end

ELBO 損失関数

関数 ELBOloss は、符号化器によって出力された平均と対数分散を受け取り、それらを使用して証拠下限 (ELBO) 損失を計算します。ELBO 損失は、2 つの個別の損失項の和によって与えられます。

$E L B O l o s s = r e c o n s t r u c t i o n l o s s + K L l o s s$ .

"再構成損失" は、復号化器の出力が元の入力にどれだけ近いかを、平均二乗誤差 (MSE) を使用して測定します。

$r e c o n s t r u c t i o n l o s s = M S E (r e c o n s t r u c t e d i m a g e, i n p u t i m a g e)$ .

"KL 損失"、つまりカルバック・ライブラーダイバージェンスは、2 つの確率分布の差を測定します。この場合、KL 損失の最小化によって、学習した平均と分散がターゲット (正規) 分布にできる限り近づくようにします。サイズ $K$ の潜在次元について、KL 損失は次のように取得されます。

$K L l o s s = - 0.5 \cdot \sum_{i = 1}^{K} (1 + \log (σ_{i}^{2}) - μ_{i}^{2} - σ_{i}^{2})$ .

KL 損失項を含めることで、再構成の損失により学習したクラスターを潜在空間の中心の周りに密集させて、サンプリング元となる連続空間を構成するという実用的な効果が得られます。

function loss = elboLoss(Y,T,mu,logSigmaSq)

% Reconstruction loss.
reconstructionLoss = mse(Y,T);

% KL divergence.
KL = -0.5 * sum(1 + logSigmaSq - mu.^2 - exp(logSigmaSq),1);
KL = mean(KL);

% Combined loss.
loss = reconstructionLoss + KL;

end

モデル予測関数

modelPredictions 関数は、符号化器と復号化器のネットワークオブジェクト、および入力データの minibatchqueue オブジェクト mbq を入力として受け取り、minibatchqueue オブジェクトのすべてのデータを反復処理することでモデル予測を計算します。

function Y = modelPredictions(netE,netD,mbq)

Y = [];

% Loop over mini-batches.
while hasdata(mbq)
    X = next(mbq);

    % Forward through encoder.
    Z = predict(netE,X);

    % Forward through decoder.
    XGenerated = predict(netD,Z);

    % Extract and concatenate predictions.
    Y = cat(4,Y,extractdata(XGenerated));
end

end

ミニバッチ前処理関数

関数 preprocessMiniBatch は、4 番目の次元に沿って入力を連結することで、予測子のミニバッチを前処理します。

function X = preprocessMiniBatch(dataX)

% Concatenate.
X = cat(4,dataX{:});

end

参考