自動微分の背景

自動微分とは

自動微分 ("autodiff"、"AD"、または "アルゴリズム的微分" とも呼ばれる) は、深層学習に広く使用されているツールです。これが特に有益なのは、最適化のために微分を手動で計算する必要なく、複雑な深層学習モデルの作成と学習を行えることです。深層学習モデル、学習ループ、および損失関数の作成とカスタマイズを行う方法を示す例については、カスタム学習ループ、損失関数、およびネットワークの定義を参照してください。

自動微分は、微分 (勾配) を数値的に評価する一連の手法です。この方法では、有限差分近似より正確な微分のシンボリック規則を使用します。純粋にシンボリックな方法とは異なり、自動微分は大規模なシンボリック計算を行うのではなく、計算の初期に式を数値的に評価します。つまり、自動微分では具体的な数値で微分が評価され、微分のシンボリック式は作成されません。

"フォワードモード" では、基本的な微分演算を、関数自体を評価する演算と同時に実行することによって、数値微分を評価します。次の節で詳しく説明するように、これらの計算は計算グラフで実行されます。
"リバースモード" の自動微分では、フォワードモードの計算グラフの拡張機能を使用して、グラフのリバース走査による勾配の計算を可能にします。コードが実行されて関数とその微分が計算されると、"トレース" と呼ばれるデータ構造に演算が記録されます。

多くの研究者が指摘しているように (たとえば、Baydin、Pearlmutter、Radul、および Siskind [1])、多くの変数のスカラー関数では、フォワードモードよりリバースモードの方が勾配の計算を効率的に行うことができます。深層学習の損失関数はすべての重みのスカラー関数であるため、Deep Learning Toolbox™ の自動微分ではリバースモードを使用します。

フォワードモード

次の関数とその勾配を評価する問題を考えます。

$f (x) = x_{1} \exp (- \frac{1}{2} (x_{1}^{2} + x_{2}^{2})) .$

自動微分は具体的な点で機能します。この場合、x₁ = 2、x₂ = 1/2 とします。

次の計算グラフは、関数 f(x) の計算を符号化します。

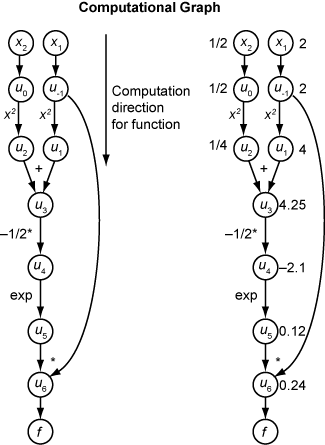
Computational graph showing the encoding of the function f(x).

フォワードモードを使用して f(x) の勾配を計算するには、同じグラフを同じ方向で計算します。ただし、微分の基本的な規則に基づいて計算に変更を加えます。計算をさらに簡略化するには、処理を進めながら各部分式 u_i の微分の値を埋めます。勾配全体を計算するには、各独立変数に関する偏微分に対して 1 回ずつ、グラフを 2 回走査しなければなりません。連鎖律の各部分式に数値があるため、式全体の評価グラフが関数自体と同じ種類になります。

計算では連鎖律が繰り返し適用されます。この例では、x₁ についての f の微分が展開されて次の式になります。

$\begin{matrix} \frac{d f}{d x_{1}} = \frac{d u_{6}}{d x_{1}} \\ = \frac{\partial u_{6}}{\partial u_{- 1}} + \frac{\partial u_{6}}{\partial u_{5}} \frac{\partial u_{5}}{\partial x_{1}} \\ = \frac{\partial u_{6}}{\partial u_{- 1}} + \frac{\partial u_{6}}{\partial u_{5}} \frac{\partial u_{5}}{\partial u_{4}} \frac{\partial u_{4}}{\partial x_{1}} \\ = \frac{\partial u_{6}}{\partial u_{- 1}} + \frac{\partial u_{6}}{\partial u_{5}} \frac{\partial u_{5}}{\partial u_{4}} \frac{\partial u_{4}}{\partial u_{3}} \frac{\partial u_{3}}{\partial x_{1}} \\ = \frac{\partial u_{6}}{\partial u_{- 1}} + \frac{\partial u_{6}}{\partial u_{5}} \frac{\partial u_{5}}{\partial u_{4}} \frac{\partial u_{4}}{\partial u_{3}} \frac{\partial u_{3}}{\partial u_{1}} \frac{\partial u_{1}}{\partial x_{1}} . \end{matrix}$

${\dot{u}}_{i}$ を使用して、x₁ についての式 u_i の微分を表します。関数評価からの u_i の評価値を使用して、次の図に示すように、x₁ についての f の偏微分を計算します。グラフを上から下に走査すると、 ${\dot{u}}_{i}$ のすべての値が使用可能になることに注目してください。

Computational graph showing the computation of the partial derivative of f with respect to x1.

x₂ についての偏微分を計算するには、同様の計算グラフを走査します。つまり、関数の勾配を計算する場合、グラフ走査の回数が変数の数と同じになります。一般的な深層学習用途では数千から数百万の変数があるため、このプロセスは非常に時間がかかります。

リバースモード

リバースモードでは、計算グラフのフォワード走査を 1 回使用してトレースを設定します。その後、反対方向にグラフを 1 回走査することによって、関数の勾配全体が計算されます。深層学習用途では、このモードの方がはるかに効率的です。

リバースモードの背景にある理論も、連鎖律と、上線付きで示す関連する随伴変数に基づいています。u_i の随伴変数は次のとおりです。

${\bar{u}}_{i} = \frac{\partial f}{\partial u_{i}} .$

計算グラフでは、変数から出ているそれぞれの矢印が、連鎖律におけるその項による、対応する随伴変数への寄与を示します。たとえば、変数 u_–1 からは 2 つの変数 u₁ および u₆ に向かって矢印が出ています。グラフには、次のような関連する方程式があります。

$\begin{matrix} \frac{\partial f}{\partial u_{- 1}} = \frac{\partial f}{\partial u_{1}} \frac{\partial u_{1}}{\partial u_{- 1}} + \frac{\partial f}{\partial u_{6}} \frac{\partial u_{6}}{\partial u_{- 1}} \\ = {\bar{u}}_{1} \frac{\partial u_{1}}{\partial u_{- 1}} + {\bar{u}}_{6} \frac{\partial u_{6}}{\partial u_{- 1}} . \end{matrix}$

$u_{1} = u_{- 1}^{2}$ および u₆ = u₅u_–1 であるため、この計算から以下が得られます。

${\bar{u}}_{- 1} = {\bar{u}}_{1} 2 u_{- 1} + {\bar{u}}_{6} u_{5} .$

グラフのフォワード走査では、中間変数 u_i が計算されます。リバース走査では、シード値 ${\bar{u}}_{6} = \frac{\partial f}{\partial f} = 1$ から始めて、リバースモードの計算によってすべての変数の随伴値が取得されます。そのため、リバースモードでは 1 回の計算で勾配が計算され、フォワードモードと比べて時間を大幅に節約できます。

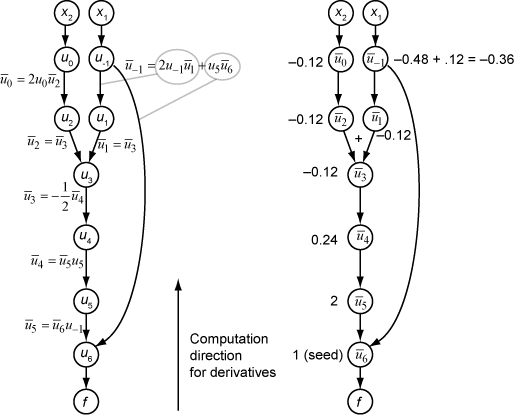
次の図は、リバースモードでの次の関数の勾配の計算を示します。

$f (x) = x_{1} \exp (- \frac{1}{2} (x_{1}^{2} + x_{2}^{2})) .$

ここでも、計算では x₁ = 2、x₂ = 1/2 とします。リバースモードの計算は、元の計算グラフでの関数の計算時に取得された u_i の値に依存します。図の右側部分では、図の左側部分の式を使用して、随伴変数の計算値を随伴変数名の横に示しています。

Computational graph showing the computation of the gradient in reverse mode for the function defined above.

最終的な勾配値は ${\bar{u}}_{0} = \frac{\partial f}{\partial u_{0}} = \frac{\partial f}{\partial x_{2}}$ および ${\bar{u}}_{- 1} = \frac{\partial f}{\partial u_{- 1}} = \frac{\partial f}{\partial x_{1}}$ となっています。

詳細は、Baydin、Pearlmutter、Radul、および Siskind [1]、または Wikipedia の自動微分に関する記事 [2] を参照してください。

参照

[1] Baydin, A. G., B. A. Pearlmutter, A. A. Radul, and J. M. Siskind. "Automatic Differentiation in Machine Learning: a Survey." The Journal of Machine Learning Research, 18(153), 2018, pp. 1–43. Available at https://arxiv.org/abs/1502.05767.

[2] Automatic differentiation. Wikipedia. Available at https://en.wikipedia.org/wiki/Automatic_differentiation.

参考

dlarray | dlgradient | dlfeval | dlnetwork