ベイズ最適化を使用した深層学習
この例では、深層学習にベイズ最適化を適用して、畳み込みニューラル ネットワークに最適なネットワーク ハイパーパラメーターと学習オプションを求める方法を説明します。
深層ニューラル ネットワークに学習させるには、ニューラル ネットワークのアーキテクチャおよび学習アルゴリズムのオプションを指定しなければなりません。これらのハイパーパラメーターの選択と調整は難しく時間がかかることがあります。ベイズ最適化は、分類モデルと回帰モデルのハイパーパラメーターの最適化に非常に適したアルゴリズムです。ベイズ最適化を使用して、微分不可能な関数、不連続な関数、および評価に時間のかかる関数を最適化できます。このアルゴリズムでは、目的関数のガウス過程モデルを内部に保持し、目的関数の評価を使用してこのモデルに学習をさせます。
この例では、以下の方法を説明します。
ネットワーク学習用の CIFAR-10 データ セットをダウンロードして準備する。このデータ セットは、イメージ分類モデルのテストに最も広く使用されているデータ セットの 1 つです。
ベイズ最適化を使用して最適化する変数を指定する。これらの変数は学習アルゴリズムのオプションであり、ネットワーク アーキテクチャ自体のパラメーターでもあります。
入力として最適化変数の値を取り、ネットワーク アーキテクチャと学習オプションを指定し、ネットワークの学習と検証を行い、学習済みネットワークをディスクに保存する目的関数を定義する。目的関数の定義は、このスクリプトの終わりで行います。
検証セットの分類誤差を最小化することにより、ベイズ最適化を実行する。
ディスクから最適なネットワークを読み込み、テスト セットに対して評価する。
代わりに、ベイズ最適化を使用し、実験マネージャーの最適な学習オプションを見つけることもできます。詳細については、Tune Experiment Hyperparameters by Using Bayesian Optimizationを参照してください。
データの準備
CIFAR-10 データ セット [1] をダウンロードします。このデータ セットには 60,000 個のイメージが格納されており、各イメージのサイズは 32 x 32 で 3 つのカラー チャネル (RGB) があります。データ セット全体のサイズは 175 MB です。インターネット接続の速度によっては、ダウンロード プロセスに時間がかかることがあります。
datadir = tempdir; downloadCIFARData(datadir);
CIFAR-10 データ セットを学習用のイメージとラベル、およびテスト用のイメージとラベルとして読み込みます。ネットワークの検証を有効にするには、検証用に 5000 個のテスト イメージを使用します。
[XTrain,YTrain,XTest,YTest] = loadCIFARData(datadir); idx = randperm(numel(YTest),5000); XValidation = XTest(:,:,:,idx); XTest(:,:,:,idx) = []; YValidation = YTest(idx); YTest(idx) = [];
次のコードを使用して、学習イメージのサンプルを表示できます。
figure; idx = randperm(numel(YTrain),20); for i = 1:numel(idx) subplot(4,5,i); imshow(XTrain(:,:,:,idx(i))); end
最適化する変数の選択
ベイズ最適化を使用して最適化する変数を選択し、検索範囲を指定します。さらに、変数が整数であるかどうか、検索区間を対数空間にするかどうかを指定します。次の変数を最適化します。
ネットワーク セクション深さ。このパラメーターはネットワークの深さを制御します。ネットワークには 3 つのセクションがあり、各セクションには
SectionDepth個の同一の畳み込み層があります。そのため、畳み込み層の総数は3*SectionDepthになります。後でスクリプトで定義する目的関数が取る各層の畳み込みフィルターの数は1/sqrt(SectionDepth)に比例します。その結果、パラメーター数と各反復に必要な計算量は、セクション深さが異なる場合でもほぼ同じになります。初期学習率。最適な学習率は、学習させるネットワークにも依りますが、データにも左右されます。
確率的勾配降下モーメンタム。モーメンタムは、前の反復での更新に比例する寄与を現在の更新に含めることによって、パラメーター更新に慣性を追加します。これにより、パラメーター更新がより円滑に行われるようになり、確率的勾配降下に固有のノイズが低減されます。
L2 正則化強度。正則化を使用して過適合を防止します。正則化強度の空間を検索して、適切な値を求めます。データ拡張やバッチ正規化も、ネットワークの正則化に役立ちます。
optimVars = [
optimizableVariable('SectionDepth',[1 3],'Type','integer')
optimizableVariable('InitialLearnRate',[1e-2 1],'Transform','log')
optimizableVariable('Momentum',[0.8 0.98])
optimizableVariable('L2Regularization',[1e-10 1e-2],'Transform','log')];ベイズ最適化の実行
学習データと検証データを入力として使用して、ベイズ オプティマイザーの目的関数を作成します。目的関数は畳み込みニューラル ネットワークに学習をさせ、検証セットに対してその分類誤差を返します。この関数の定義は、このスクリプトの終わりで行います。bayesopt は検証セットの誤差率を使用して最適なモデルを選択するため、最終的なネットワークが検証セットに過適合する可能性があります。そのため、最終的に選択されたモデルを独立したテスト セットでテストして、汎化誤差を推定します。
ObjFcn = makeObjFcn(XTrain,YTrain,XValidation,YValidation);
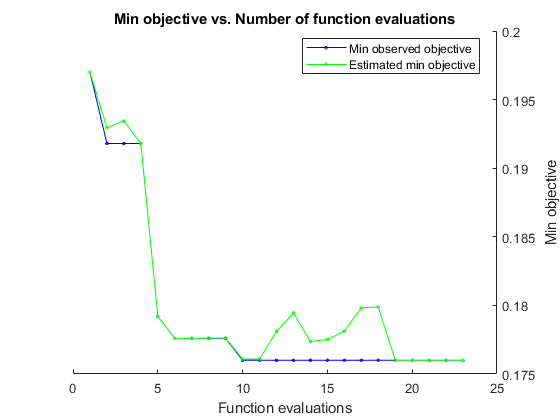
検証セットの分類誤差を最小化することにより、ベイズ最適化を実行する。合計最適化時間を秒単位で指定します。ベイズ最適化の能力を最大限に活用するには、目的関数の評価を 30 回以上行う必要があります。複数の GPU でネットワークの並列学習を行うには、'UseParallel' の値を true に設定します。GPU が 1 つで、'UseParallel' の値を true に設定した場合、すべてのワーカーがその GPU を共有するため、学習を高速化できず、GPU のメモリ不足が発生する可能性が高まります。
ネットワークの学習が完了するたびに、bayesopt によってコマンド ウィンドウに結果が表示されます。その後、関数 bayesopt が BayesObject.UserDataTrace にファイル名を返します。目的関数は学習済みネットワークをディスクに保存し、bayesopt にファイル名を返します。
BayesObject = bayesopt(ObjFcn,optimVars, ... 'MaxTime',14*60*60, ... 'IsObjectiveDeterministic',false, ... 'UseParallel',false);
|===================================================================================================================================| | Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | SectionDepth | InitialLearn-| Momentum | L2Regulariza-| | | result | | runtime | (observed) | (estim.) | | Rate | | tion | |===================================================================================================================================| | 1 | Best | 0.197 | 955.69 | 0.197 | 0.197 | 3 | 0.61856 | 0.80624 | 0.00035179 |
| 2 | Best | 0.1918 | 790.38 | 0.1918 | 0.19293 | 2 | 0.074118 | 0.91031 | 2.7229e-09 |
| 3 | Accept | 0.2438 | 660.29 | 0.1918 | 0.19344 | 1 | 0.051153 | 0.90911 | 0.00043113 |
| 4 | Accept | 0.208 | 672.81 | 0.1918 | 0.1918 | 1 | 0.70138 | 0.81923 | 3.7783e-08 |
| 5 | Best | 0.1792 | 844.07 | 0.1792 | 0.17921 | 2 | 0.65156 | 0.93783 | 3.3663e-10 |
| 6 | Best | 0.1776 | 851.49 | 0.1776 | 0.17759 | 2 | 0.23619 | 0.91932 | 1.0007e-10 |
| 7 | Accept | 0.2232 | 883.5 | 0.1776 | 0.17759 | 2 | 0.011147 | 0.91526 | 0.0099842 |
| 8 | Accept | 0.2508 | 822.65 | 0.1776 | 0.17762 | 1 | 0.023919 | 0.91048 | 1.0002e-10 |
| 9 | Accept | 0.1974 | 1947.6 | 0.1776 | 0.17761 | 3 | 0.010017 | 0.97683 | 5.4603e-10 |
| 10 | Best | 0.176 | 1938.4 | 0.176 | 0.17608 | 2 | 0.3526 | 0.82381 | 1.4244e-07 |
| 11 | Accept | 0.1914 | 2874.4 | 0.176 | 0.17608 | 3 | 0.079847 | 0.86801 | 9.7335e-07 |
| 12 | Accept | 0.181 | 2578 | 0.176 | 0.17809 | 2 | 0.35141 | 0.80202 | 4.5634e-08 |
| 13 | Accept | 0.1838 | 2410.8 | 0.176 | 0.17946 | 2 | 0.39508 | 0.95968 | 9.3856e-06 |
| 14 | Accept | 0.1786 | 2490.6 | 0.176 | 0.17737 | 2 | 0.44857 | 0.91827 | 1.0939e-10 |
| 15 | Accept | 0.1776 | 2668 | 0.176 | 0.17751 | 2 | 0.95793 | 0.85503 | 1.0222e-05 |
| 16 | Accept | 0.1824 | 3059.8 | 0.176 | 0.17812 | 2 | 0.41142 | 0.86931 | 1.447e-06 |
| 17 | Accept | 0.1894 | 3091.5 | 0.176 | 0.17982 | 2 | 0.97051 | 0.80284 | 1.5836e-10 |
| 18 | Accept | 0.217 | 2794.5 | 0.176 | 0.17989 | 1 | 0.2464 | 0.84428 | 4.4938e-06 |
| 19 | Accept | 0.2358 | 4054.2 | 0.176 | 0.17601 | 3 | 0.22843 | 0.9454 | 0.00098248 |
| 20 | Accept | 0.2216 | 4411.7 | 0.176 | 0.17601 | 3 | 0.010847 | 0.82288 | 2.4756e-08 |
|===================================================================================================================================| | Iter | Eval | Objective | Objective | BestSoFar | BestSoFar | SectionDepth | InitialLearn-| Momentum | L2Regulariza-| | | result | | runtime | (observed) | (estim.) | | Rate | | tion | |===================================================================================================================================| | 21 | Accept | 0.2038 | 3906.4 | 0.176 | 0.17601 | 2 | 0.09885 | 0.81541 | 0.0021184 |
| 22 | Accept | 0.2492 | 4103.4 | 0.176 | 0.17601 | 2 | 0.52313 | 0.83139 | 0.0016269 |
| 23 | Accept | 0.1814 | 4240.5 | 0.176 | 0.17601 | 2 | 0.29506 | 0.84061 | 6.0203e-10 |
__________________________________________________________
Optimization completed.
MaxTime of 50400 seconds reached.
Total function evaluations: 23
Total elapsed time: 53088.5123 seconds
Total objective function evaluation time: 53050.7026
Best observed feasible point:
SectionDepth InitialLearnRate Momentum L2Regularization
____________ ________________ ________ ________________
2 0.3526 0.82381 1.4244e-07
Observed objective function value = 0.176
Estimated objective function value = 0.17601
Function evaluation time = 1938.4483
Best estimated feasible point (according to models):
SectionDepth InitialLearnRate Momentum L2Regularization
____________ ________________ ________ ________________
2 0.3526 0.82381 1.4244e-07
Estimated objective function value = 0.17601
Estimated function evaluation time = 1898.2641
最終的なネットワークの評価
最適化で見つかった最適なネットワークと、その検証精度を読み込みます。
bestIdx = BayesObject.IndexOfMinimumTrace(end);
fileName = BayesObject.UserDataTrace{bestIdx};
savedStruct = load(fileName);
valError = savedStruct.valErrorvalError = 0.1760
テスト セットのラベルを予測して、テスト誤差を計算します。テスト セットの各イメージの分類を特定の成功確率を持つ独立事象として扱います。これは、誤って分類されるイメージの数が二項分布に従うことを意味します。これを使用して、標準誤差 (testErrorSE) と、汎化誤差率の近似した 95% 信頼区間 (testError95CI) を計算します。この方法は通常、"Wald 法" と呼ばれます。bayesopt は、ネットワークにテスト セットを当てることなく、検証セットを使用して最適なネットワークを決定します。これにより、テスト誤差が検証誤差より高くなる可能性があります。
[YPredicted,probs] = classify(savedStruct.trainedNet,XTest); testError = 1 - mean(YPredicted == YTest)
testError = 0.1910
NTest = numel(YTest); testErrorSE = sqrt(testError*(1-testError)/NTest); testError95CI = [testError - 1.96*testErrorSE, testError + 1.96*testErrorSE]
testError95CI = 1×2
0.1801 0.2019
テスト データの混同行列をプロットします。列と行の要約を使用して、各クラスの適合率と再現率を表示します。
figure('Units','normalized','Position',[0.2 0.2 0.4 0.4]); cm = confusionchart(YTest,YPredicted); cm.Title = 'Confusion Matrix for Test Data'; cm.ColumnSummary = 'column-normalized'; cm.RowSummary = 'row-normalized';

次のコードを使用して、いくつかのテスト イメージを、予測されたクラスとそのクラスである確率と共に表示できます。
figure idx = randperm(numel(YTest),9); for i = 1:numel(idx) subplot(3,3,i) imshow(XTest(:,:,:,idx(i))); prob = num2str(100*max(probs(idx(i),:)),3); predClass = char(YPredicted(idx(i))); label = [predClass,', ',prob,'%']; title(label) end
最適化の目的関数
最適化の目的関数を定義します。この関数は、以下の手順を実行します。
入力として最適化変数の値を取ります。
bayesoptは、各列の名前が変数名と等しい table に含まれる最適化変数の現在の値を使用して、目的関数を呼び出します。たとえば、ネットワーク セクション深さの現在の値はoptVars.SectionDepthです。ネットワーク アーキテクチャと学習オプションを定義します。
ネットワークの学習と検証を行います。
学習済みネットワーク、検証誤差、および学習オプションをディスクに保存します。
検証誤差と保存されたネットワークのファイル名を返します。
function ObjFcn = makeObjFcn(XTrain,YTrain,XValidation,YValidation) ObjFcn = @valErrorFun; function [valError,cons,fileName] = valErrorFun(optVars)
畳み込みニューラル ネットワーク アーキテクチャを定義します。
空間の出力サイズが入力サイズと常に同じになるように、畳み込み層にパディングを追加します。
最大プーリング層を使用して係数 2 で空間次元をダウンサンプリングするたびに、フィルターの数を 2 倍ずつ増加させます。それにより、各畳み込み層で必要な計算量がほぼ同じになります。
フィルターの数を
1/sqrt(SectionDepth)に比例するように選択し、深さの異なるネットワークにほぼ同じ数のパラメーターがあり、反復ごとにほぼ同じ量の計算が必要になるようにします。ネットワーク パラメーターの数を増やし、ネットワーク全体の柔軟性を高めるには、numFを大きくします。さらに深いネットワークに学習させるには、変数SectionDepthの範囲を変更します。convBlock(filterSize,numFilters,numConvLayers)を使用して、numConvLayers個の畳み込み層のブロックを作成します。各層にはfilterSizeのnumFilters個のフィルターを指定し、それぞれの後にバッチ正規化層と ReLU 層を配置します。関数convBlockの定義は、この例の終わりで行います。
imageSize = [32 32 3];
numClasses = numel(unique(YTrain));
numF = round(16/sqrt(optVars.SectionDepth));
layers = [
imageInputLayer(imageSize)
% The spatial input and output sizes of these convolutional
% layers are 32-by-32, and the following max pooling layer
% reduces this to 16-by-16.
convBlock(3,numF,optVars.SectionDepth)
maxPooling2dLayer(3,'Stride',2,'Padding','same')
% The spatial input and output sizes of these convolutional
% layers are 16-by-16, and the following max pooling layer
% reduces this to 8-by-8.
convBlock(3,2*numF,optVars.SectionDepth)
maxPooling2dLayer(3,'Stride',2,'Padding','same')
% The spatial input and output sizes of these convolutional
% layers are 8-by-8. The global average pooling layer averages
% over the 8-by-8 inputs, giving an output of size
% 1-by-1-by-4*initialNumFilters. With a global average
% pooling layer, the final classification output is only
% sensitive to the total amount of each feature present in the
% input image, but insensitive to the spatial positions of the
% features.
convBlock(3,4*numF,optVars.SectionDepth)
averagePooling2dLayer(8)
% Add the fully connected layer and the final softmax and
% classification layers.
fullyConnectedLayer(numClasses)
softmaxLayer
classificationLayer];ネットワーク学習のオプションを指定します。初期学習率、SGD モーメンタム、および L2 正則化強度を最適化します。
検証データを指定し、trainNetwork によってエポックごとに 1 回ネットワークが検証されるように、'ValidationFrequency' の値を選択します。一定のエポック数の学習を行い、最後の方のエポックでは学習率を 10 分の 1 に下げます。これにより、パラメーター更新のノイズが減少し、ネットワーク パラメーターが安定して損失関数が最小値に近づくようになります。
miniBatchSize = 256;
validationFrequency = floor(numel(YTrain)/miniBatchSize);
options = trainingOptions('sgdm', ...
'InitialLearnRate',optVars.InitialLearnRate, ...
'Momentum',optVars.Momentum, ...
'MaxEpochs',60, ...
'LearnRateSchedule','piecewise', ...
'LearnRateDropPeriod',40, ...
'LearnRateDropFactor',0.1, ...
'MiniBatchSize',miniBatchSize, ...
'L2Regularization',optVars.L2Regularization, ...
'Shuffle','every-epoch', ...
'Verbose',false, ...
'Plots','training-progress', ...
'ValidationData',{XValidation,YValidation}, ...
'ValidationFrequency',validationFrequency);データ拡張を使用して、縦軸に沿って学習イメージをランダムに反転させ、水平方向および垂直方向に最大 4 ピクセルだけランダムに平行移動させます。データ拡張は、ネットワークで過適合が発生したり、学習イメージの正確な詳細が記憶されたりすることを防止するのに役立ちます。
pixelRange = [-4 4];
imageAugmenter = imageDataAugmenter( ...
'RandXReflection',true, ...
'RandXTranslation',pixelRange, ...
'RandYTranslation',pixelRange);
datasource = augmentedImageDatastore(imageSize,XTrain,YTrain,'DataAugmentation',imageAugmenter);ネットワークに学習させ、学習中にその進行状況をプロットします。学習が終了したら、すべての学習プロットを閉じます。
trainedNet = trainNetwork(datasource,layers,options);
close(findall(groot,'Tag','NNET_CNN_TRAININGPLOT_UIFIGURE'))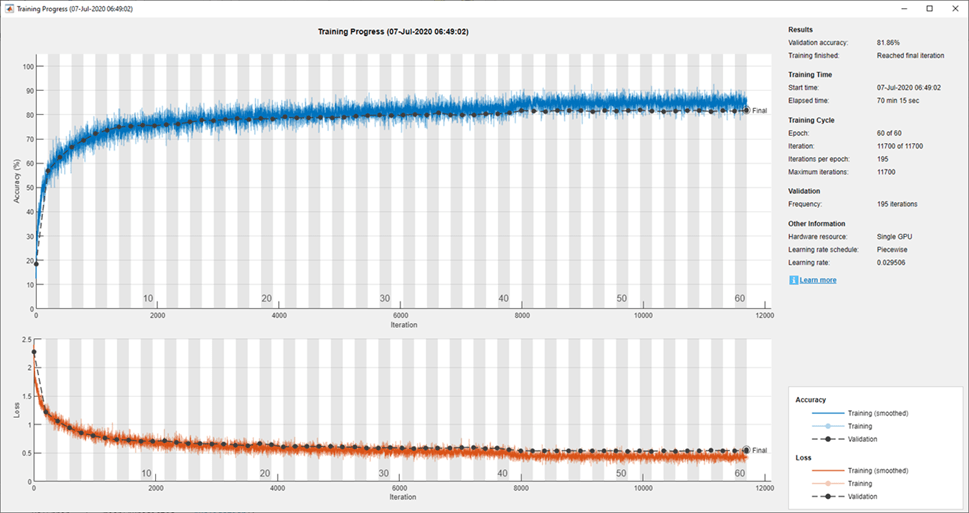
検証セットに対して学習済みネットワークを評価して、予測イメージ ラベルを計算し、検証データにおける誤差率を計算します。
YPredicted = classify(trainedNet,XValidation);
valError = 1 - mean(YPredicted == YValidation);検証誤差を含むファイル名を作成し、ネットワーク、検証誤差、および学習オプションをディスクに保存します。目的関数は出力引数として fileName を返し、bayesopt は BayesObject.UserDataTrace にすべてのファイル名を返します。別途要求された出力引数 cons は、変数間の制約を指定します。変数の制約はありません。
fileName = num2str(valError) + ".mat"; save(fileName,'trainedNet','valError','options') cons = []; end end
関数 convBlock は、numConvLayers 個の畳み込み層のブロックを作成します。各層には filterSize の numFilters 個のフィルターを指定し、それぞれの後にバッチ正規化層と ReLU 層を配置します。
function layers = convBlock(filterSize,numFilters,numConvLayers) layers = [ convolution2dLayer(filterSize,numFilters,'Padding','same') batchNormalizationLayer reluLayer]; layers = repmat(layers,numConvLayers,1); end
参照
[1] Krizhevsky, Alex. "Learning multiple layers of features from tiny images." (2009). https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf
参考
実験マネージャー | trainnet | trainingOptions | dlnetwork | bayesopt (Statistics and Machine Learning Toolbox)