有理モデル

"有理モデル" は次で与えられる多項式の比で、"有理関数" と呼ばれることもあります。

$y = \frac{\sum_{i = 1}^{n + 1} p_{i} x^{n + 1 - i}}{x^{m} + \sum_{i = 1}^{m} q_{i} x^{m - 1}},$

ここで、n は分子多項式の次数、m は分母多項式の次数です。Curve Fitting Toolbox™ では、0 ≤ n ≤ 5 および 1 ≤ m ≤ 5 の有理モデルをサポートしています。x^m に関連する係数は常に 1 です。これにより、多項式の次数が同じ場合、分子と分母は一意に決まります。

ここでは、有理式を分子の次数/分母の次数に着目して記述します。たとえば、2 次/3 次の有理方程式は次で与えられます

$y = \frac{p_{1} x^{2} + p_{2} x + p_{3}}{x^{3} + q_{1} x^{2} + q_{2} x + q_{3}}$

簡単な経験的モデルが必要な場合、多項式と同様に有理式がよく使用されます。有理式の主な利点は、構造が複雑なデータに対する柔軟性です。主な欠点は、分母が 0 に近づくと不安定になることです。さまざまな次数の有理多項式を使用する例については、例: 有理近似を参照してください。

有理モデルによる対話的な近似

MATLAB^® コマンドラインで curveFitter と入力して曲線フィッターアプリを開きます。または、[アプリ] タブの [数学、統計および最適化] グループで [曲線フィッター] をクリックします。
曲線フィッターアプリで、曲線データを選択します。[曲線フィッター] タブの [データ] セクションで [データの選択] をクリックします。[近似データの選択] ダイアログボックスで、[X データ] および [Y データ] を選択するか、インデックスに対する [Y データ] のみを選択します。
[近似タイプ] セクションの矢印をクリックしてギャラリーを開き、[回帰モデル] グループの [有理] をクリックします。

Fit Options pane for rational fit

[近似オプション] ペインで、次のオプションを指定できます。

分子の次数には範囲 [0 5] 内の非負の整数を指定し、分母の次数には範囲 [1 5] 内の正の整数を指定します。[結果] ペインを参照し、モデル項、係数の値、適合度の統計量を確認します。
必要に応じて、[詳細オプション] セクションで係数の開始値と制約範囲を指定するか、アルゴリズム設定を変更します。区間 [0 1] で定義される、有理モデルのランダムな開始点がアプリによって計算されます。開始点をオーバーライドして、[近似オプション] ペインで独自の値を指定することができます。

設定の詳細については、近似オプションと最適化された開始点の指定を参照してください。

コマンドラインでの有理近似の選択

モデルタイプとして ratij を指定します。ここで、i は分子多項式の次数であり、j は分母多項式の次数です。たとえば、'rat02'、'rat21'、'rat55' のようにします。

たとえば、データを読み込んで有理モデルで近似するには次のようにします。

load hahn1;
f = fit( temp, thermex, 'rat32')
plot(f,temp,thermex)

さまざまな有理モデルを使用してこの例を対話的に近似する方法については、例: 有理近似を参照してください。

係数の開始値や制約範囲などの近似オプションをデータに合わせて変更したり、アルゴリズム設定を変更したりする場合は、fitoptions のリファレンスページにある NonlinearLeastSquares の追加プロパティの表を参照してください。

例: 有理近似

この例では、有理近似を使用して熱膨張データに当てはめます。このデータは、ケルビン単位の温度の関数としての銅の熱膨張係数を表しています。

有理近似は、次によって与えられる多項式の比として定義されます。

$y = \frac{p_{1} x^{n} + p_{2} x^{n - 1} + ... + p_{n + 1}}{x^{m} + q_{1} x^{m - 1} + ... + q_{m}}$

ここで、n は分子多項式の次数であり、m は分母多項式の次数です。有理方程式は、データの物理的なパラメーターには関連付けられていません。その代わり、内挿や外挿に使用できる簡単で経験的なモデルを提供します。

hahn1 の熱膨張データを読み込みます。このデータセットには、ケルビン単位の温度のベクトル (temp) と、銅の熱膨張係数のベクトル (thermex) が含まれています。
```
load hahn1
```
曲線フィッターアプリを開きます。
```
curveFitter
```
または、[アプリ] タブの [数学、統計および最適化] グループで [曲線フィッター] をクリックします。
曲線フィッターアプリで、曲線データを選択します。[曲線フィッター] タブの [データ] セクションで [データの選択] をクリックします。[近似データの選択] ダイアログボックスで、[X データ] に temp を指定し、[Y データ] に thermex を指定します。曲線フィッターアプリにより、曲線データに当てはめられプロットされます。
[近似タイプ] セクションの矢印をクリックしてギャラリーを開き、[回帰モデル] グループの [有理] をクリックします。
2 次/2 次の有理近似を試します。[近似オプション] ペインで、[分子の次数] と [分母の次数] の両方に 2 を選択します。
近似の名前を変更します。[近似テーブル] ペインで、[近似名] の値をダブルクリックして rat22 と入力します。
[可視化] セクションで [残差プロット] を選択します。データ、近似および残差を検証します。この近似は予測子の最小値と最大値に対応するデータから外れていることを観察します。また、この残差はデータセット全体で強いパターンを示しています。こうした観測から、より適切な近似が可能であることがわかります。
3 次/3 次の有理近似を試します。まず、現在の近似を複製します。[曲線フィッター] タブの [ファイル] セクションで [複製] をクリックします。新しい近似に rat33 という名前を付けます。
[近似オプション] ペインで、[分子の次数] と [分母の次数] の両方に 3 を選択します。データ、近似および残差を検証します。
メモ
結果はランダムな開始点に依存するため、ここに示した結果と異なる場合があります。近似は、分母がゼロに近いところでいくつかの不連続点を示すことがあります。
[結果] ペインを見てみます。このメッセージと数値結果は、近似が収束しなかったことを示します。
[結果] ペインのメッセージは、最大反復回数を増やすと近似が改善する可能性があることを示していますが、近似プロセスのこの段階では異なる有理方程式を使用することが良い選択となります。
3 次/2 次の有理近似を試します。まず、現在の近似を複製します。[曲線フィッター] タブの [ファイル] セクションで [複製] をクリックします。新しい近似に rat32 という名前を付けます。
[近似オプション] ペインで、[分子の次数] と [分母の次数] に、それぞれ 3 と 2 を選択します。
データ変数間のスケールが大きく異なるため、[データのセンタリングとスケーリング] チェックボックスをオンにします。データ、近似、残差を次に示します。
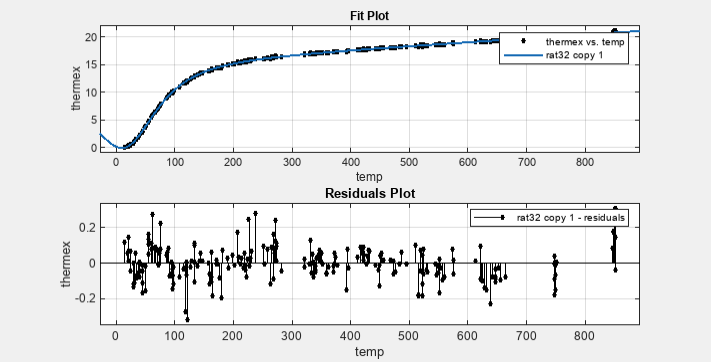
この近似は、データ範囲全体でうまく機能し、残差はゼロ付近にランダムに散っています。そのため、確信をもってこの近似でさらに解析を進めることができます。