2-DOF PID コントローラーの調整 (コマンド ライン)
この例では、2 自由度 (2-DOF) PID コントローラーをコマンド ラインで設計する方法を示します。また、この例では 2-DOF コントローラーの性能を 1-DOF PID コントローラーで達成されている性能と比較します。
2-DOF PID コントローラーには、比例項および微分項に設定点の重みが含まれています。1-DOF PID コントローラーと比較すると、2-DOF PID コントローラーでは、設定点の追従でオーバーシュートを大幅に増加させることなく、さらに優れた外乱の抑制が達成されます。2-DOF PID コントローラーを使用した典型的な制御アーキテクチャを次の図に示します。

この例では、次の式で与えられるプラントの 2-DOF コントローラーを設計します。
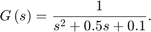
システムでターゲットとする帯域幅を 1.5 rad/s とします。
wc = 1.5;
G = tf(1,[1 0.5 0.1]);
C2 = pidtune(G,'PID2',wc)
C2 =
1
u = Kp (b*r-y) + Ki --- (r-y) + Kd*s (c*r-y)
s
with Kp = 1.26, Ki = 0.255, Kd = 1.38, b = 0.665, c = 0
Continuous-time 2-DOF PID controller in parallel form.
タイプ 'PID2' を使用すると、pidtune により 2-DOF コントローラーが生成され、pid2 オブジェクトとして表現されます。表示からこの結果が確認されます。pidtune は、設定点の重み b および c を含めてすべてのコントローラー係数を調整して、性能とロバスト性のバランスを取ります。
閉ループ応答を計算する際は、2-DOF PID コントローラーが 2 入力 1 出力の動的システムであることに注意してください。コントローラーは、2 つのチャネルに関連付けることができます。図に示すとおり、1 つは基準信号、もう 1 つはフィードバック信号のチャネルです (詳細については、連続時間 2-DOF PID コントローラーの表現を参照してください。)

コントローラーをコンポーネント Cr および Cy に分解し、r から y への閉ループ応答の計算に使用します。
C2tf = tf(C2); Cr = C2tf(1); Cy = C2tf(2); T2 = Cr*feedback(G,Cy,+1);
外乱の抑制の性能を調べるには、d から y への伝達関数を計算します。
S2 = feedback(G,Cy,+1);
比較のため、同じ帯域幅の 1-DOF PID コントローラーを設計し、対応する伝達関数を計算します。それからステップ応答を比較します。
C1 = pidtune(G,'PID',wc); T1 = feedback(G*C1,1); S1 = feedback(G,C1); subplot(2,1,1) stepplot(T1,T2) title('Reference Tracking') subplot(2,1,2) stepplot(S1,S2) title('Disturbance Rejection') legend('1-DOF','2-DOF')

プロットでは、2 つ目の自由度を追加すると、外乱の抑制をまったく犠牲にせずに設定値追従応答でのオーバーシュートが除去されることが示されています。外乱の抑制も DesignFocus オプションを使用して改善できます。このオプションにより、pidtune は設定点の追従よりも外乱の抑制を優先するようになります。
opt = pidtuneOptions('DesignFocus','disturbance-rejection'); C2dr = pidtune(G,'PID2',wc,opt)
C2dr =
1
u = Kp (b*r-y) + Ki --- (r-y) + Kd*s (c*r-y)
s
with Kp = 1.72, Ki = 0.593, Kd = 1.25, b = 0, c = 0
Continuous-time 2-DOF PID controller in parallel form.
バランスを取った既定の設計フォーカスの場合、pidtune は b の値を 0 と 1 の間で選択します。このプラントで、設計フォーカスを変更して外乱の抑制を優先すると、pidtune は b = 0 および c = 0 に設定します。このように、pidtune は I-PD コントローラーを自動生成し、外乱の抑制用に最適化します (設計フォーカスを設定せず、明示的に I-PD コントローラーを指定しても、同様のコントローラーが生成されます。)
3 つのコントローラーをすべて使用して閉ループ応答を比較します。
C2dr_tf = tf(C2dr); Cdr_r = C2dr_tf(1); Cdr_y = C2dr_tf(2); T2dr = Cdr_r*feedback(G,Cdr_y,+1); S2dr = feedback(G,Cdr_y,+1); subplot(2,1,1) stepplot(T1,T2,T2dr) title('Reference Tracking') subplot(2,1,2) stepplot(S1,S2,S2dr); title('Disturbance Rejection') legend('1-DOF','2-DOF','2-DOF rejection focus')

プロットでは、バランスの取れた 2-DOF コントローラーと比較して、外乱の抑制がさらに改善されていることが示されています。この改善には、設定値追従がわずかに遅くなるという性能上のいくらかの犠牲が伴います。しかし、この場合も、設定値追従の応答にオーバーシュートはありません。
したがって、2-DOF 制御を使用することで、設定値追従の性能を 1-DOF 制御ほど犠牲にすることなく、外乱の抑制を改善できます。システムの性能に対するこれらの効果は、プラントの特性に強く左右されます。プラントや制御帯域幅によっては、2-DOF 制御の使用や設計フォーカスの変更は、調整結果にほとんど、あるいはまったく影響を与えません。