カート上の倒立振子の制御
この例では、カート上の倒立振子を制御するために systune を使用します。
振子/カート アセンブリ
図 1 に示されているカート/振子アセンブリは、Simscape™ Multibody™ を使用して Simulink® でモデル化されます。

図 1: カート上の倒立振子

図 2: Simscape Multibody モデル
このシステムは、カートに可変の力 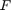 をかけることで制御されます。カートを新しい位置に移動させる間、あるいは振子が前方に軽く押された (インパルス外乱
をかけることで制御されます。カートを新しい位置に移動させる間、あるいは振子が前方に軽く押された (インパルス外乱  ) とき、コントローラーは振子を直立させておく必要があります。
) とき、コントローラーは振子を直立させておく必要があります。
制御構造
垂直位置は倒立振子にとっては不安定な平衡状態です。プラントがもつ不安定な特性によって、制御タスクはより難しくなっています。この例では、次のような 2 ループの制御構造を使用します。
open_system('rct_pendulum.slx') set_param('rct_pendulum','SimMechanicsOpenEditorOnUpdate','off');

内側のループは 2 次状態空間コントローラーを使用して振子を垂直位置に安定化させますが ( コントロール)、外側のループは比例-微分 (PD) コントローラーを使用してカートの位置を制御します。プラントが既にいくつかの積分動作を提供しているため、PID ではなく PD コントローラーを使用します。
コントロール)、外側のループは比例-微分 (PD) コントローラーを使用してカートの位置を制御します。プラントが既にいくつかの積分動作を提供しているため、PID ではなく PD コントローラーを使用します。
設計要件
TuningGoal 要件を使用して、目的の閉ループ動作を指定します。カート位置  での設定点の変化に追従するために、応答時間 3 秒を指定します。
での設定点の変化に追従するために、応答時間 3 秒を指定します。
% Tracking of x command req1 = TuningGoal.Tracking('xref','x',3);
振子の先端でのインパルス外乱  を適切に抑制するには、次の形式の LQR ペナルティを使用します。
を適切に抑制するには、次の形式の LQR ペナルティを使用します。
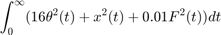
これにより、小さな角度偏差  が強調され、制御操作
が強調され、制御操作 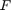 が制限されます。
が制限されます。
% Rejection of impulse disturbance dF Qxu = diag([16 1 0.01]); req2 = TuningGoal.LQG('dF',{'Theta','x','F'},1,Qxu);
ロバスト性を実現するには、プラント入力に少なくとも 6 dB のゲイン余裕と 40 度の位相余裕が必要です。
% Stability margins req3 = TuningGoal.Margins('F',6,40);
最後に、閉ループ極の減衰と固有振動数を制約し、ぎくしゃくした動きの、もしくは不足減衰の過渡特性を防ぎます。
% Pole locations
MinDamping = 0.5;
MaxFrequency = 45;
req4 = TuningGoal.Poles(0,MinDamping,MaxFrequency);
制御システムの調整
閉ループ システムは、PD コントローラーと状態空間コントローラーの初期値 (それぞれ、1 と 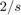 ) に対して不安定です。
) に対して不安定です。systune を使用して、これら 2 つのコントローラーを一緒に調整できます。slTuner インターフェイスを使用して調整可能なブロックを指定し、安定余裕を測定するための解析ポイントとしてプラント入力 F を登録します。
ST0 = slTuner('rct_pendulum',{'Position Controller','Angle Controller'}); addPoint(ST0,'F');
次に、systune を使用し、上で指定した性能要件に従って PD コントローラーと状態空間コントローラーを調整します。安定余裕と極の位置の制約 (厳密な要件) に従って、追従および外乱抑制性能 (柔軟な要件) を最適化します。
rng(0)
Options = systuneOptions('RandomStart',5);
[ST, fSoft] = systune(ST0,[req1,req2],[req3,req4],Options);
Final: Soft = 1.36, Hard = 0.99737, Iterations = 341 Final: Soft = 1.44, Hard = 0.99942, Iterations = 155 Final: Soft = 1.44, Hard = 0.99919, Iterations = 330 Final: Soft = 1.26, Hard = 0.99809, Iterations = 267 Final: Soft = 1.44, Hard = 0.9993, Iterations = 268 Final: Soft = 1.26, Hard = 0.99972, Iterations = 233
最適な設計は、厳密な要件 (Hard<1) を満たすと同時に、柔軟な要件について 1 に近い値を達成します。つまり、調整された制御システムは、安定余裕および極の位置の制約を満たしながら、追従と外乱抑制における目標性能をほぼ達成します。
検証
viewGoal を使用して、最適な設計が各要件に対してどのようにふるまうかをさらに解析します。
figure('Position',[100 100 575 660])
viewGoal([req1,req3,req4],ST)

最後の 2 つの要件が厳密に適用されている間は最初の 2 つの要件がほぼ満たされていることが、これらのプロットによって確認できます。次に、その位置のステップ変化とカート上の力インパルスに対する応答をプロットします。
T = getIOTransfer(ST,{'xref','dF'},{'x','Theta'});
figure('Position',[100 100 650 420]);
subplot(121), step(T(:,1),10)
title('Tracking of set point change in position')
subplot(122), impulse(T(:,2),10)
title('Rejection of impulse disturbance')
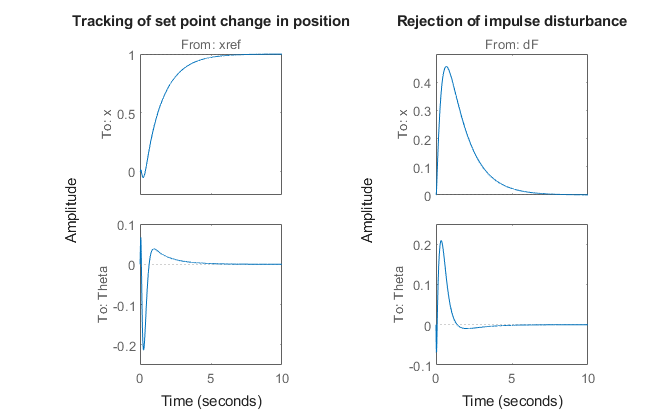
目的の整定時間での応答は滑らかです。コントローラーの調整済みの値を検証します。
C1 = getBlockValue(ST,'Position Controller')
C1 =
s
Kp + Kd * --------
Tf*s+1
with Kp = 6.11, Kd = 2.19, Tf = 0.0536
Name: Position_Controller
Continuous-time PDF controller in parallel form.
C2 = zpk(getBlockValue(ST,'Angle Controller'))
C2 =
-1638.9 (s+12.73) (s+4.551)
---------------------------
(s+136) (s-14.52)
Name: Angle_Controller
Continuous-time zero/pole/gain model.
角度コントローラーには不安定な極があり、プラントの不安定な極と組み合わせることで倒立振子を安定化させていることに注意してください。これを確認するには、プラント入力で開ループ伝達を取得し、根軌跡をプロットします。
L = getLoopTransfer(ST,'F',-1); figure rlocus(L) set(gca,'XLim',[-25 20],'YLim',[-20 20])

検証を完了するには、調整された値を Simulink にアップロードし、カート/振子アセンブリの非線形応答をシミュレートします。シミュレーション結果のビデオが下に表示されます。
writeBlockValue(ST)

図 3: 調整コントローラーを使用したカート/振子のシミュレーション。
シミュレーション後にモデルを閉じます。
set_param('rct_pendulum','SimMechanicsOpenEditorOnUpdate','on'); close_system('rct_pendulum',0);
参考
systune (Simulink Control Design) | slTuner (Simulink Control Design)
トピック
- 制御システムの解析と設計における対象信号のマーク (Simulink Control Design)
- Simulink モデルに対する slTuner インターフェイスの作成と設定 (Simulink Control Design)