Simulink での LQR サーボ コントローラーの設計

この例では、航空機の自動操縦アプリケーションを使用した Simulink® での LQR サーボ コントローラーの設計を示します。

航空機モデルを開きます。

open_system("lqrpilot")

このモデルには次の項目が含まれています。

• Linearized Dynamics ブロックには、線形化された機体が含まれる。

• sf_aerodyn は、$\left(\theta ,\varphi \right)=\left(0,{15}^{\circ }\right)$ に対する非線形方程式を含んだ S-Function ブロックである。

• $\varphi$ と ${\varphi }_{\mathrm{ref}}$ の間の誤差信号は、誤差をゼロにするのに役立つ積分器を通過する。

モデルを開くと、lqrpilotData MAT ファイルも読み込まれます。このファイルには以下のデータが含まれています。

• 状態方程式行列 A および B

• 線形化された状態行列 A15

• 最終 LQG ゲイン行列 K_lqr

航空機状態空間方程式

方程式は状態空間システムの標準状態方程式です。

$$\dot{\mathit{x}}=\mathit{A}\mathit{x}+\mathit{B}\mathit{u}$$

航空機システムでは、状態ベクトルは次のとおりです。

$$\mathit{x}={\left[\mathit{u},\mathit{v},\mathit{w},\mathit{p},\mathit{q},\mathit{r},\theta ,\varphi \right]}^{\mathit{T}}$$

下図に示されているように、変数 $\mathit{u}$、$\mathit{v}$、$\mathit{w}$ は、機体座標系に関連した 3 つの速度です。

変数 $\varphi$ および $\theta$ はロールとピッチです。$\mathit{p}$、$\mathit{q}$、および $\mathit{r}$ は、それぞれロール、ピッチ、ヨーのレートです。

機体のダイナミクスは非線形です。次の方程式は、状態空間方程式に追加された非線形コンポーネントを示します。ここで、$\mathit{g}$ は重力による加速度です。

$$\dot{\mathit{x}}=\mathit{Ax}+\mathit{Bu}+\left[\begin{array}{c}-\mathit{g}\cdot \sin \theta \\ \mathit{g}\cdot \cos \theta \cdot \sin \varphi \\ \mathit{g}\cdot \cos \theta \cdot \cos \varphi \\ 0\\ 0\\ 0\\ \mathit{q}\cdot \cos \varphi -\mathit{r}\cdot \sin \varphi \\ \left(\mathit{q}\cdot \sin \varphi +\mathit{r}\cdot \cos \varphi \right)\cdot \tan \theta \end{array}\right]$$

平衡化

LQG 設計目的で、非線形ダイナミクスは $\varphi ={15}^{\circ }$ で平衡化され、$\mathit{p}$、$\mathit{q}$、$\mathit{r}$、および $\theta$ は 0 に設定されています。前の方程式で $\mathit{u}$、$\mathit{v}$、および $\mathit{w}$ は非線形項に影響しないため、結果は $\left(\theta ,\varphi \right)=\left(0,{15}^{\circ }\right)$ 付近で線形化されたモデルになり、その他すべての状態はゼロとなります。

lqrdes スクリプトは、この平衡化された操作点で線形化されたモデル A15 を計算する方法を示しています。

問題定義

設計の目標は、この図のように安定した旋回を行うことです。

ここでは、60°のロールで安定した旋回を制御するコントローラーを設計します。さらに、ピッチ角度 $\theta$ が、できるだけゼロに近い状態を続ける必要があるとします。

結果

lqrdes スクリプトは、LQG ゲイン行列 K_lqr を計算する方法を示しています。

lqrpilot モデルで、Nonlinear Dynamics ブロックの出力を選択するように Switch ブロックが構成されていることを確認します。

モデルを実行します。

sim("lqrpilot")

ステップ変更 60° に対するロール $\varphi$ の応答を確認します。システムが指令されたロールに約 60 秒以内にトラッキングしています。

open_system("lqrpilot/phi (roll angle)")

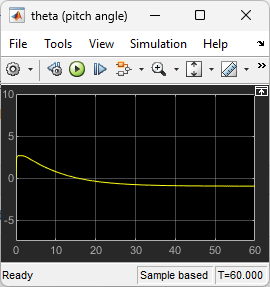
ピッチ角 $\theta$ を確認します。コントローラーは、ピッチ角を比較的小さく保つことができました。

open_system("lqrpilot/theta (pitch angle)")

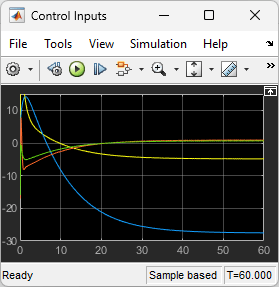
最後に、制御入力を確認します。

open_system("lqrpilot/Control Inputs")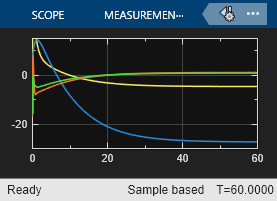

lqrdes スクリプトで Q と R の値を調整して、考えられるさまざまな設計を試すことができます。また、線形システムと非線形システムのダイナミクスのシミュレーションを比較すると、システムの性能に対する非線形の効果を確認できます。

関連するトピック

• カルマン フィルター処理
• 線形 2 次ガウシアン (LQG) 設計
• LQG レギュレーターの設計
• LQG サーボ コントローラーの設計