カルマン フィルター処理

この例では、カルマン フィルター処理を実行する方法を示します。最初に、kalman コマンドを使用して定常状態フィルターを設計します。次に、システムをシミュレートして、測定ノイズから誤差を低減する方法を示します。また、時変フィルターを実装する方法も説明します。時変フィルターは、非定常ノイズ源をもつシステムで役に立ちます。

定常状態カルマン フィルター

入力にガウス ノイズ "w" および出力に測定ノイズ "v" をもつ次の離散プラントを考えます。

$$\begin{array}{c}x\left[n+1\right]=Ax\left[n\right]+Bu\left[n\right]+Gw\left[n\right]\\ y\left[n\right]=Cx\left[n\right]+Du\left[n\right]+Hw\left[n\right]+v\left[n\right]\end{array}$$

目標は、カルマン フィルターを設計し、ノイズ測定量 $\mathit{y}\left[\mathit{n}\right]$ に基づいて真のプラント出力 ${\mathit{y}}_{\mathit{t}}\left[\mathit{n}\right]=\mathit{y}\left[\mathit{n}\right]-\mathit{v}\left[\mathit{n}\right]$ を推定することです。この定常状態カルマン フィルターでは、この推定に次の方程式を使用します。

時刻の更新:

$\hat{\mathit{x}}\left[\mathit{n}+1|\mathit{n}\right]=\mathit{A}\hat{\mathit{x}}\left[\mathit{n}|\mathit{n}-1\right]+\mathit{Bu}\left[\mathit{n}\right]+\mathit{Gw}\left[\mathit{n}\right]$

測定値の更新:

$$\begin{array}{l}\underset{}{\overset{ˆ}{x}}\left[n|n\right]=\underset{}{\overset{ˆ}{x}}\left[n|n-1\right]+M_x\left(y\left[n\right]-C\underset{}{\overset{ˆ}{x}}\left[n|n-1\right]-Du\left[n\right]\right)\\ \underset{}{\overset{ˆ}{y}}\left[n|n\right]=C\underset{}{\overset{ˆ}{x}}\left[n|n-1\right]+Du\left[n\right]+M_y\left(y\left[n\right]-C\underset{}{\overset{ˆ}{x}}\left[n|n-1\right]-Du\left[n\right]\right)\end{array}$$

ここで

• $\hat{\mathit{x}}\left[\mathit{n}|\mathit{n}-1\right]$ は、$\mathit{y}\left[\mathit{n}-1\right]$ までの過去の測定値からの $\mathit{x}\left[\mathit{n}\right]$ の推定値。

• $\hat{\mathit{x}}\left[\mathit{n}|\mathit{n}\right]$ および $\hat{\mathit{y}}\left[\mathit{n}|\mathit{n}\right]$ は、最後の測定値 $\mathit{y}\left[\mathit{n}\right]$ に基づいて更新された、推定された状態値と測定値。

• ${\mathit{M}}_{\mathit{x}}$ および ${\mathit{M}}_{\mathit{y}}$ は、ノイズ共分散 $\mathit{E}\left(\mathit{w}\left[\mathit{n}\right]{\mathit{w}\left[\mathit{n}\right]}^{\mathit{T}}\right)=\mathit{Q}$、$\mathit{E}\left(\mathit{v}\left[\mathit{n}\right]{\mathit{v}\left[\mathit{n}\right]}^{\mathit{T}}\right)=\mathit{R}$、および $\mathit{N}=\mathit{E}\left(\mathit{w}\left[\mathit{n}\right]{\mathit{v}\left[\mathit{n}\right]}^{\mathit{T}}\right)=0$ に対する推定誤差の定常状態共分散を最小にするように選択された、最適なイノベーション ゲイン (これらのゲインの選択方法の詳細については、kalman を参照)。

(これらの方程式は、current タイプの推定器を表します。current 推定器と delayed 推定器の違いについては、kalmanを参照してください。)

フィルターの設計

関数 kalman を使用すると、定常状態カルマン フィルターを設計できます。この関数は、指定したプロセス ノイズの共分散 "Q" とセンサー ノイズの共分散 "R" に基づいて、特定のプラントに対して最適な定常状態フィルターのゲイン "M" を判定します。この例では、プラントの状態空間行列に対して次の値を使用します。

A = [1.1269   -0.4940    0.1129 
     1.0000         0         0 
          0    1.0000         0];

B = [-0.3832
      0.5919
      0.5191];

C = [1 0 0];

D = 0;

この例では、$\mathit{G}=\mathit{B}$ と設定します。つまり、プロセス ノイズ "w" は加法的入力ノイズになります。また、$\mathit{H}=0$ と設定します。これは入力ノイズ "w" が出力 "y" に直接影響しないことを意味します。これらの仮定により、次のシンプルなプラント モデルが生成されます。

$$\begin{array}{c}x\left[n+1\right]=Ax\left[n\right]+Bu\left[n\right]+Bw\left[n\right]\\ y\left[n\right]=Cx\left[n\right]+v\left[n\right]\end{array}$$

H = 0 の場合、${\mathit{M}}_{\mathit{y}}=\mathit{C}{\mathit{M}}_{\mathit{x}}$ となります (kalmanを参照)。また、これらの仮定により、カルマン フィルターの更新方程式も簡略化されます。

時刻の更新:

$\hat{\mathit{x}}\left[\mathit{n}+1|\mathit{n}\right]=\mathit{A}\hat{\mathit{x}}\left[\mathit{n}|\mathit{n}-1\right]+\mathit{Bu}\left[\mathit{n}\right]+\mathit{Bw}\left[\mathit{n}\right]$

測定値の更新:

$$\begin{array}{l}\underset{}{\overset{ˆ}{x}}\left[n|n\right]=\underset{}{\overset{ˆ}{x}}\left[n|n-1\right]+M_x\left(y\left[n\right]-C\underset{}{\overset{ˆ}{x}}\left[n|n-1\right]\right)\\ \underset{}{\overset{ˆ}{y}}\left[n|n\right]=C\underset{}{\overset{ˆ}{x}}\left[n|n\right]\end{array}$$

このフィルターを設計するには、最初に w の入力をもつプラント モデルを作成します。サンプル時間を -1 に設定してプラントを離散系 (特定のサンプル時間を指定しない) としてマークします。

Ts = -1;
sys = ss(A,[B B],C,D,Ts,'InputName',{'u' 'w'},'OutputName','y');  % Plant dynamics and additive input noise w

プロセス ノイズの共分散 Q とセンサー ノイズの共分散 R は、通常はシステムの学習値または測定値から取得する、0 より大きい値です。この例では、次の値を指定します。

Q = 2.3; 
R = 1; 

kalman コマンドを使用してフィルターを設計します。

[kalmf,L,~,Mx,Z] = kalman(sys,Q,R);

このコマンドでカルマン フィルター kalmf、つまり時刻の更新の方程式と測定値の更新の方程式を実装する状態空間モデルを設計します。フィルター入力は、プラント入力 "u" およびノイズを含むプラント出力 "y" です。kalmf の最初の出力は、真のプラント出力の推定 $\hat{\mathit{y}}$ で、残りの出力は状態推定 $\hat{\mathit{x}}$ です。

この例では、状態推定を破棄し、最初の出力 $\hat{\mathit{y}}$ のみを保持します。

kalmf = kalmf(1,:);

フィルターの使用

このフィルターの機能を確認するために、データを生成し、フィルターを適用した応答を真のプラント応答と比較します。完全なシステムを次のブロック線図に示します。

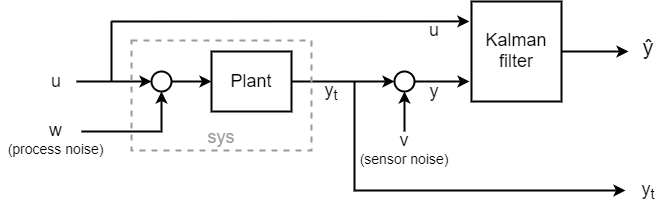
このシステムをシミュレートするには、sumblk を使用して測定ノイズ v の入力を作成します。次に、connect を使用して sys とカルマン フィルターを連結し、u が共有入力となり、ノイズを含むプラント出力 y が他のフィルター入力に送られるようにします。結果は、入力 w、v、u と出力 yt (真の応答) および ye (フィルターまたは推測された応答 $\hat{\mathit{y}}$) をもつシミュレーション モデルになります。信号 yt と ye はそれぞれ、プラントとフィルターの出力になります。

sys.InputName = {'u','w'};
sys.OutputName = {'yt'};
vIn = sumblk('y=yt+v');

kalmf.InputName = {'u','y'};
kalmf.OutputName = 'ye';

SimModel = connect(sys,vIn,kalmf,{'u','w','v'},{'yt','ye'});

フィルターの挙動をシミュレーションするには、既知の正弦波入力ベクトルを生成します。

t = (0:100)';
u = sin(t/5);

フィルターを設計したときに使用したものと同じノイズ共分散値 Q と R を使って、プロセス ノイズ ベクトルとセンサー ノイズ ベクトルを生成します。

rng(10,'twister');
w = sqrt(Q)*randn(length(t),1);
v = sqrt(R)*randn(length(t),1);

最後に lsim を使用して応答のシミュレーションを実行します。

out = lsim(SimModel,[u,w,v]);

lsim では、w、v、u で適用された入力に対する出力 yt と ye における応答が生成されます。yt および ye チャネルを抽出して、測定された応答を計算します。

yt = out(:,1);   % true response
ye = out(:,2);  % filtered response
y = yt + v;     % measured response

真の応答をフィルターを適用した応答と比較します。

clf
subplot(211), plot(t,yt,'b',t,ye,'r--'), 
xlabel('Number of Samples'), ylabel('Output')
title('Kalman Filter Response')
legend('True','Filtered')
subplot(212), plot(t,yt-y,'g',t,yt-ye,'r--'),
xlabel('Number of Samples'), ylabel('Error')
legend('True - measured','True - filtered')

2 番目のプロットに示すように、カルマン フィルターは測定ノイズによる誤差 yt - y を低減します。この低減を確認するには、フィルター適用前 (測定誤差の共分散) とフィルター適用後 (推定誤差の共分散) の誤差の共分散を計算します。

MeasErr = yt - y;
MeasErrCov = sum(MeasErr.*MeasErr)/length(MeasErr)

MeasErrCov = 
0.9871

EstErr = yt - ye;
EstErrCov = sum(EstErr.*EstErr)/length(EstErr)

EstErrCov = 
0.3479

時変カルマン フィルターの設計

前の設計では、ノイズ共分散は時間が経過しても変動しないものと仮定していました。時変カルマン フィルターは、ノイズの共分散が定常的でないときでも良好に動作します。

時変カルマン フィルターには次の更新方程式があります。時変フィルターでは、誤差の共分散 $\mathit{P}\left[\mathit{n}\right]$ とイノベーション ゲイン ${\mathit{M}}_{\mathit{x}}\left[\mathit{n}\right]$ の両方が時間とともに変動する可能性があります。次のように時刻および測定値更新方程式を変更して、時間の変動を考慮できます。ここでも、$\mathit{G}=\mathit{B}$ とし、プロセス ノイズ "w" が加法的入力ノイズになるようにします。

時刻の更新:

$$\begin{array}{l}\underset{}{\overset{ˆ}{x}}\left[n+1|n\right]=A\underset{}{\overset{ˆ}{x}}\left[n|n\right]+Bu\left[n\right]+Bw\left[n\right]\\ P\left[n+1|n\right]=AP\left[n|n\right]A^T+BQ{B}^T\end{array}$$

測定値の更新:

$$\begin{array}{l}\underset{}{\overset{ˆ}{x}}\left[n|n\right]=\underset{}{\overset{ˆ}{x}}\left[n|n-1\right]+M_x\left[n\right]\left(y\left[n\right]-C\underset{}{\overset{ˆ}{x}}\left[n|n-1\right]\right)\\ M_x\left[n\right]=P\left[n|n-1\right]C^T{\left(CP\left[n|n-1\right]C^T+R\left[n\right]\right)}^{-1}\\ P\left[n|n\right]=\left(I-M_x\left[n\right]C\right)P\left[n|n-1\right]\\ \underset{}{\overset{ˆ}{y}}\left[n|n\right]=C\underset{}{\overset{ˆ}{x}}\left[n|n\right]\end{array}$$

これらの式の詳細については、kalmanを参照してください。

Simulink® で、Kalman Filterブロックを使用して時変カルマン フィルターを実装できます (時変のカルマン フィルターを使用した状態推定を参照)。

MATLAB® で時変カルマン フィルターを作成するには、まず、ノイズのあるプラント応答を生成します。前に定義した入力信号 u とプロセス ノイズ w へのプラント応答をシミュレーションします。次に、測定ノイズ v をシミュレートされた真の応答 yt に追加してノイズのある応答 y を取得します。この例では、ノイズ ベクトル w および v の共分散は時間とともに変動していません。ただし、同じ手順は非定常ノイズに使用できます。

yt = lsim(sys,[u w]);   
y = yt + v;         

次に、for ループ内で再帰フィルターの更新方程式を実装します。

P = B*Q*B';         % Initial error covariance
x = zeros(3,1);     % Initial condition on the state

ye = zeros(length(t),1);
ycov = zeros(length(t),1); 
errcov = zeros(length(t),1); 

for i=1:length(t)
  % Measurement update
  Mxn = P*C'/(C*P*C'+R);
  x = x + Mxn*(y(i)-C*x);   % x[n|n]
  P = (eye(3)-Mxn*C)*P;     % P[n|n]

  ye(i) = C*x;
  errcov(i) = C*P*C';

  % Time update
  x = A*x + B*u(i);        % x[n+1|n]
  P = A*P*A' + B*Q*B';     % P[n+1|n] 
end

真の応答をフィルターを適用した応答と比較します。

subplot(211), plot(t,yt,'b',t,ye,'r--')
xlabel('Number of Samples'), ylabel('Output')
title('Response with Time-Varying Kalman Filter')
legend('True','Filtered')
subplot(212), plot(t,yt-y,'g',t,yt-ye,'r--'),
xlabel('Number of Samples'), ylabel('Error')
legend('True - measured','True - filtered')

時変フィルターは、推定中に出力共分散も推定します。この例では定常入力ノイズを使用するため、出力共分散は定常値になる傾向にあります。フィルターが定常状態に達していることを確認するために、出力共分散をプロットします。

figure
plot(t,errcov) 
xlabel('Number of Samples'), ylabel('Error Covariance'),

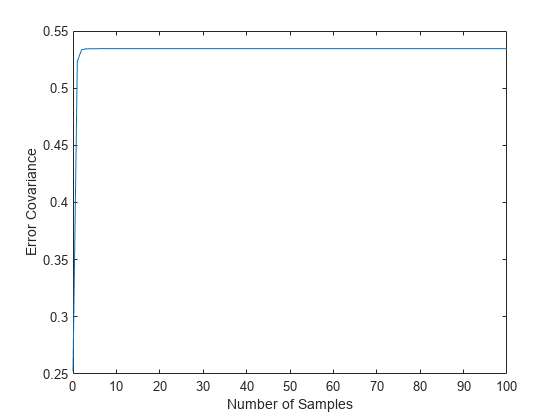
共分散プロットから、出力共分散がおよそ 5 つのサンプルで定常状態に達したことを確認できます。それ以降、時変フィルターは定常状態バージョンと同じ性能を維持します。

定常状態の例に示すように、フィルターは測定ノイズによる誤差を低減します。この低減を確認するには、フィルター適用前 (測定誤差の共分散) とフィルター適用後 (推定誤差の共分散) の誤差の共分散を計算します。

MeasErr = yt - y;
MeasErrCov = sum(MeasErr.*MeasErr)/length(MeasErr)

MeasErrCov = 
0.9871

EstErr = yt - ye;
EstErrCov = sum(EstErr.*EstErr)/length(EstErr)

EstErrCov = 
0.3479

最後に、時変フィルターが定常状態に達すると、ゲイン行列 Mxn の値は、定常状態フィルターの kalman で計算された値に一致します。

Mx,Mxn

Mx = 3×1

    0.5345
    0.0101
   -0.4776

Mxn = 3×1

    0.5345
    0.0101
   -0.4776

カルマン フィルターの詳細

カルマン フィルターの詳細については、ビデオをご覧になるか、Understanding Kalman Filters — MATLAB Tech Talks の残りのシリーズをご覧ください。

参考

kalman

関連するトピック

• 時変のカルマン フィルターを使用した状態推定
• LQG レギュレーター: 圧延機のケース スタディ

外部の Web サイト

• Understanding Kalman Filters — MATLAB ビデオ シリーズ