LQG レギュレーターの設計

LQG 設計の例として、次の制御問題について考えます。

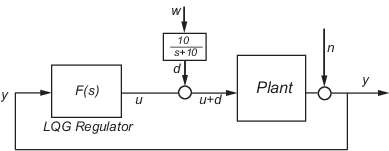
目標は、プラント出力 y をゼロ近傍で調節することです。入力外乱 d は、10 rad/s 未満に集中したパワースペクトル密度 (PSD) を含む低周波です。次の図に示すように、LQG 設計用に、カットオフ 10 rad/s のローパスフィルターがホワイトノイズで励起されるとしてモデル化されています。

設計を簡単にするために、このノイズは分散が 1 のガウスのホワイトノイズとしてモデル化されています。

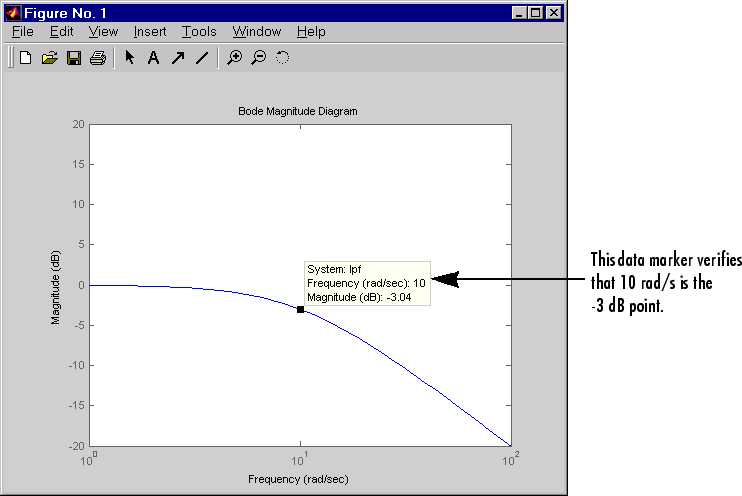
次の図は、整形フィルターのボード振幅を示します。

ローパスフィルターのボード振幅

次の式で与えられる強度を含む測定ノイズ n が存在します。

$E (n^{2}) = 0.01$

以下のコスト関数を使用して、

$J (u) = \int_{0}^{\infty} (10 y^{2} + u^{2}) d t$

レギュレーションの性能と制御のコストのトレードオフを指定します。次の方程式は、開ループの状態空間モデルを表します。

$\begin{array}{l} \dot{x} = A x + B u + B d (s t a t e e q u a t i o n s) \\ y = C x + n (m e a s u r e m e n t s) \end{array}$

ここで、(A、B、C) は $100 / (s^{2} + s + 100)$ の状態空間実現です。

次のコマンドは、この問題に対するオプションの LQG レギュレーター F(s) を設計します。

sys = ss(tf(100,[1 1 100])) % State-space plant model

% Design LQ-optimal gain K
K = lqry(sys,10,1)	 % u = -Kx minimizes J(u)

% Separate control input u and disturbance input d
P = sys(:,[1 1]);
% input [u;d], output y

% Design Kalman state estimator Kest.
Kest = kalman(P,1,0.01)

% Form LQG regulator = LQ gain + Kalman filter.
F = lqgreg(Kest,K)

これらのコマンドは、LQG レギュレーター F(s) の状態空間モデル F を出力します。関数 lqry、kalman、lqgreg を離散プラントに適用した場合は、離散時間 LQG が設計されます。

設計を検証するために、関数 feedback でループを閉じて、閉ループシステムでローパスフィルターを作成して追加し、関数 impulse を使用して、開ループと閉ループのインパルス応答を比較します。

% Close loop
clsys = feedback(sys,F,+1)
% Note positive feedback.

% Create the lowpass filter and add it in series with clsys.
s = tf('s');
lpf= 10/(s+10) ;
clsys_fin = lpf*clsys;

% Open- vs. closed-loop impulse responses
impulse(sys,'r--',clsys_fin,'b-')

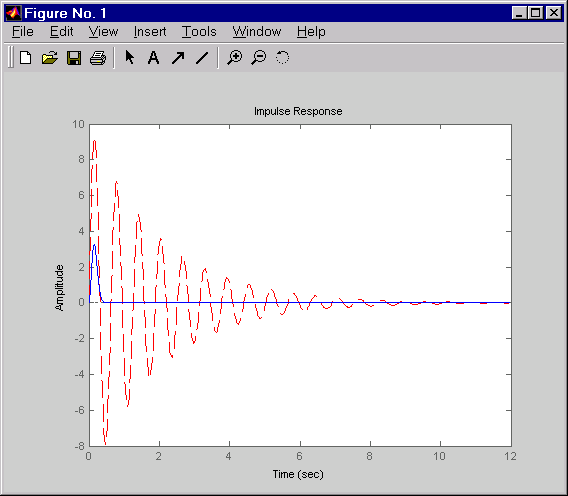
これらのコマンドでは、この例の開ループと閉ループのインパルス応答を比較する次の図が生成されます。

開ループと閉ループのインパルス応答の比較

参考

kalman | lqgreg

LQG レギュレーターの設計

参考

関連するトピック