このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

アンテナ カップリングによる OSTBC 送信

この例では、アンテナの相互カップリングが多入力多出力 (MIMO) チャネルでの直交空間時間ブロック符号 (OSTBC) の伝送のパフォーマンスに与える影響を示します。送信機と受信機はそれぞれ 2 つの双極子アンテナ素子を持ちます。BER 対 SNR 曲線が、さまざまな相関およびカップリングのシナリオでプロットされます。この例を実行するには、Antenna Toolbox™ が必要です。

システム パラメーター

QPSK 変調された Alamouti OSTBC を準静的かつ周波数フラットな 2x2 レイリー チャネル [1] でシミュレートします。システムは 2.4 GHz で動作します。シミュレートする SNR+ の範囲は 0 から 10 dB です。

fc = 2.4e9;         % Center frequency
Nt = 2;             % Number of Tx antennas
Nr = 2;             % Number of Rx antennas
blkLen = 2;         % Alamouti code block length
snr = 0:10;         % SNR range
maxNumErrs = 3e2;   % Maximum number of errors
maxNumBits = 5e4;   % Maximum number of bits

QPSK の変調と復調、Alamouti 符号化と組み合わせ、AWGN チャネルおよびBER 計算を組み合わせるオブジェクトを作成します。

qpskMod = comm.QPSKModulator;
qpskDemod = comm.QPSKDemodulator; 
alamoutiEnc = comm.OSTBCEncoder( ...
    'NumTransmitAntennas', Nt);
alamoutiDec = comm.OSTBCCombiner( ...
    'NumTransmitAntennas', Nt, ...
    'NumReceiveAntennas',  Nr);
awgnChanNC = comm.AWGNChannel( ... % For no coupling case
    'NoiseMethod', 'Signal to noise ratio (SNR)',...
    'SignalPower', 1);
berCalcNC = comm.ErrorRate;       % For no coupling case

% Clone objects for mutual coupling case 
awgnChanMC = clone(awgnChanNC); 
berCalcMC  = clone(berCalcNC);

アンテナ アレイとカップリングの行列

2 要素の共振双極子配列は、送信 (Tx) 側と受信 (Rx) 側の両方で使用されます。Tx 側では、双極子は半波長間隔で配置されます。Rx 側では、間隔は波長の 1/10 です。

txSpacing = 0.5;
rxSpacing = 0.1;
lambda = physconst('lightspeed')/fc;
antElement = dipole( ...
    'Length', lambda/2, ...
    'Width',  lambda/100);
txArray = linearArray( ...
    'Element',        antElement,...
    'NumElements',    Nt,...
    'ElementSpacing', txSpacing*lambda);
rxArray = linearArray( ...
    'Element',        antElement,...
    'NumElements',    Nr,...
    'ElementSpacing', rxSpacing*lambda);

カップリング行列は、[2] のアレイの回路モデルをベースにして計算されます。S パラメーターの計算は、送信アレイと受信アレイで実行され、これからアレイのインピーダンス行列表現が求められます。

txMCMtx = helperCalculateCouplingMatrix(txArray, fc, [1 Nt]);
rxMCMtx = helperCalculateCouplingMatrix(rxArray, fc, [1 Nr]);

空間相関行列

送信および受信空間相関行列は、チャネルの伝播環境をキャプチャします。カップリングしない場合は、Tx 側の 2 要素は相関せず、Rx 側の 2 要素の相関が高くなります。チャネル全体の組み合わせた/全体の相関行列は、そのクロネッカーの積です。

txCorrMtx = eye(2);
rxCorrMtx = [1 0.9; 0.9 1];
combCorrMtx = kron(txCorrMtx, rxCorrMtx);

カップリングした場合は、[3] のアプローチを使用し、対応するカップリング行列で事前または事後に乗算することで Tx と Rx の相関行列を変更します。これは、相関とカップリングは個別にモデル化できるという仮定の下で有効です。

txMCCorrMtx = txMCMtx * txCorrMtx * txMCMtx';
rxMCCorrMtx = rxMCMtx * rxCorrMtx * rxMCMtx';

カップリングと組み合わせた空間相関は kron(txMCCorr, rxMCCorr) となります。または、Tx/Rx カップリング行列を Tx/Rx 相関行列に "吸収" されると考えて、組み合わされた相関行列を次のように求めることができます。

txSqrtCorrMtx = txMCMtx * sqrtm(txCorrMtx);
rxSqrtCorrMtx = rxMCMtx * sqrtm(rxCorrMtx);
combMCCorrMtx = kron(txSqrtCorrMtx, rxSqrtCorrMtx);
combMCCorrMtx = combMCCorrMtx * combMCCorrMtx';

MIMO チャネルのモデル化

2 つのcomm.MIMOChannelオブジェクトを作成して、カップリングする場合としない場合で 2x2 MIMO チャネルをシミュレーションします。それぞれの場合に、組み合わせた空間相関行列を割り当てます。オブジェクトの MaximumDopplerShift プロパティを 0 に設定して、準静的なチャネルをモデル化します。

mimoChanNC = comm.MIMOChannel( ...  % For no coupling case 
    'MaximumDopplerShift',             0, ...
    'SpatialCorrelationSpecification', 'Combined', ...
    'SpatialCorrelationMatrix',        combCorrMtx,...
    'PathGainsOutputPort',             true);

% Clone objects for mutual coupling case 
mimoChanMC = clone(mimoChanNC);
mimoChanMC.SpatialCorrelationMatrix = combMCCorrMtx;

シミュレーション

アンテナ カップリングをする場合としない場合で、各 SNR 値の QPSK 変調 Alamouti コードをシミュレーションします。Alamouti コードは、各反復で MIMO チャネル経由でシミュレーションされます。準静的なチャネルをモデル化するために、comm.MIMOChannel オブジェクトをリセットして各コード伝送 (反復) の新しいチャネル ゲインのセットを取得します。

% Set up a figure to visualize BER results
h1 = figure; grid on; hold on;
ax = gca;
ax.YScale = 'log';
xlim([snr(1), snr(end)]); ylim([1e-3 1]);
xlabel('SNR (dB)'); ylabel('BER'); 
h1.NumberTitle = 'off';
h1.Name = 'Orthogonal Space-Time Block Coding';
h1.Renderer = 'zbuffer';
title('Alamouti-coded 2x2 System - High Coupling, High Correlation');

s = rng(108);  % For repeatability
[berNC, berMC] = deal(zeros(3,length(snr)));

% Loop over SNR values
for idx = 1:length(snr)
    awgnChanNC.SNR = snr(idx); 
    awgnChanMC.SNR = snr(idx); 
    reset(berCalcNC); 
    reset(berCalcMC);    
    
    while min(berNC(2,idx),berMC(2,idx)) <= maxNumErrs && (berNC(3,idx) <= maxNumBits)    
        % Generate random data
        txData = randi([0 3], blkLen, 1);
        
        % Perform QPSK modulation and Alamouti encoding
        txSig = alamoutiEnc(qpskMod(txData)); 
        
        % Pass through MIMO channel
        reset(mimoChanNC); reset(mimoChanMC);
        [chanOutNC, estChanNC] = mimoChanNC(txSig);
        [chanOutMC, estChanMC] = mimoChanMC(txSig);
        
        % Add AWGN
        rxSigNC = awgnChanNC(chanOutNC);
        rxSigMC = awgnChanMC(chanOutMC);
        
        % Perform Alamouti decoding with known channel state information
        decSigNC = alamoutiDec(rxSigNC, squeeze(estChanNC));
        decSigMC = alamoutiDec(rxSigMC, squeeze(estChanMC));
                        
        % Perform QPSK demodulation 
        rxDataNC = qpskDemod(decSigNC);
        rxDataMC = qpskDemod(decSigMC);
        
        % Update BER
        berNC(:, idx) = berCalcNC(txData, rxDataNC);
        berMC(:, idx) = berCalcMC(txData, rxDataMC);
    end 

    % Plot results
    semilogy(snr(1:idx), berNC(1,1:idx), 'r*');
    semilogy(snr(1:idx), berMC(1,1:idx), 'bo');
    legend({'Channel Without Coupling', 'Channel With Coupling'});
    drawnow;
end

% Perform curve fitting
fitBERNC = berfit(snr, berNC(1,:));
fitBERMC = berfit(snr, berMC(1,:));
semilogy(snr, fitBERNC, 'r', snr, fitBERMC, 'b');
legend({'Channel Without Coupling', 'Channel With Coupling'});

rng(s); % Restore RNG

その他の調査

BER パフォーマンスにおける相関と相互カップリングの影響は、相関係数を変更したり要素の間隔を変更したりすることで詳しく確認できます。カップリングは間隔が小さいほど大きくなります。Rx における高相関 (0.9) と高カップリング (spacing = $$0.1\lambda$$) について上記で行ったのと同様に、今度は低相関 (0.1) および/または低カップリング (spacing = $$0.5\lambda$$) についての BER 対 SNR の結果を示します。

• 高カップリング (spacing = $$0.1\lambda$$)、低相関 (0.1)

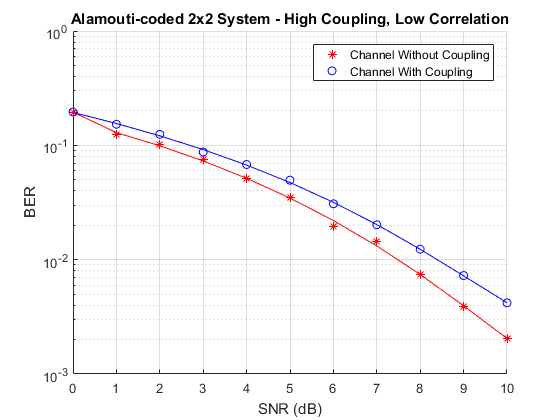
• 低カップリング (spacing = $$0.5\lambda$$)、高相関 (0.9)

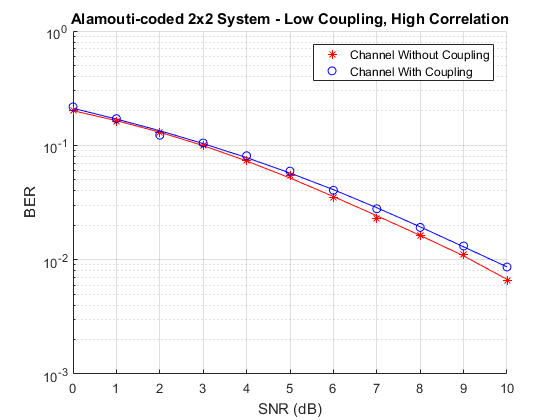
• 低カップリング (spacing = $$0.5\lambda$$)、低相関 (0.1)

まとめ

シミュレーションの結果は、[1] で報告されているものと似ています。$$0.5\lambda$$ の間隔にすると、相関条件が高い場合と低い場合の両方で BER にわずかな影響があります。高カップリング、すなわち $$0.1\lambda$$ 要素間隔の場合の結果は、相関条件によって、カップリングを考慮しなかった場合よりも BER が高くなるか低くなる場合があることを示しています。

付録

この例では、以下の補助関数を使用します。

• helperCalculateCouplingMatrix.m

参考文献

1 - A. A. Abouda, H. M. El-Sallabi, and S. G. Haggman, "Effect of Mutual Coupling on BER Performance of Alamouti Scheme," IEEE International Symposium on Antennas and Propagation, July 2006.

2 - I. J. Gupta and A. A. Ksienski, "Effect of mutual coupling on the performance of adaptive arrays," IEEE Trans. on Antennas and Propagation, vol. 31, no. 5, pp. 785-791, 1989.

3 - Y. Wu, J. P. Linnartz, J. W. M. Bergmans, and S. Attallah, "Effects of Antenna Mutual Coupling on the Performance of MIMO Systems," Proc.29th Symposium on Information Theory in the Benelux, May 2008.