差分パルス符号変調

スカラー量子化では、送信される信号に関する事前の知識を必要としない方法が使用されます。実際には、多くの場合、過去の信号送信に基づいて現在の信号に関して経験に基づく推定を行うことができます。経験に基づく推定を使って信号を量子化することを "予測量子化" といいます。差分パルス符号変調 (DPCM) は、最も一般的な予測量子化方式です。dpcmenco 関数、dpcmdeco 関数、および dpcmopt 関数を使用すると、線形予測子を使用して DPCM 予測量子化器を実装できます。

予測子の表現

量子化器の DPCM 符号化器を決定するには、量子化で説明した分割とコードブックだけでなく、"予測子" を指定しなければなりません。 予測子は、各手順で経験に基づく推定を行うために DPCM 符号化器が使用する関数です。線形予測子は、以下の形式です。

y(k) = p(1)x(k-1) + p(2)x(k-2) + ... + p(m-1)x(k-m+1) + p(m)x(k-m)
ここで、x は元の信号を表し、y(k) は x(k) の値を予測します。p は実数の m 組です。x 自身を量子化する代わりに、DPCM 符号化器は、"予測誤差" x-y を量子化します。上記の整数 m は、"予測次数" と呼ばれます。m = 1 である特殊な場合は、"デルタ変調" と呼ばれます。

x の以前の値に基づく信号 x の k 番目の値の推定が次のように表される場合を考えてみます。

y(k) = p(1)x(k-1) + p(2)x(k-2) +...+ p(m-1)x(k-m+1) + p(m)x(k-m)

ツールボックス関数に対応する予測子ベクトルは次のベクトルになります。

predictor = [0, p(1), p(2), p(3),..., p(m-1), p(m)]

メモ

予測子ベクトルの最初の 0 は、ベクトルを有限インパルス応答 (FIR) フィルターの多項式伝達関数として考えると理解できます。

DPCM の符号化と復号化を使用した信号の量子化

ライブ スクリプトを開く

DPCM の符号化と復号化を使用して、現在の信号サンプルの値と前のサンプルの値の差を量子化します。この例では、予測子 y(k)=x(k-1) を使用します。次に、ノコギリ波信号を符号化して復号化し、元の信号と復号化された信号の両方をプロットし、元の信号と復号化された信号の間の平均二乗誤差を計算します。

partition = [-1:.1:.9];
codebook = [-1:.1:1];
predictor = [0 1];      % y(k)=x(k-1)
t = [0:pi/50:2*pi];     % Time samples
x = sawtooth(3*t);      % Original signal

DPCM 符号化を使用して x を量子化します。

encodedx = dpcmenco(x,codebook,partition,predictor);

DPCM 復号化を使用して、変調信号から x を復元します。元の信号と復号化された信号をプロットします。実線は元の信号を示し、破線は復元された信号を示します。

decodedx = dpcmdeco(encodedx,codebook,predictor);
plot(t,x,t,decodedx,'-')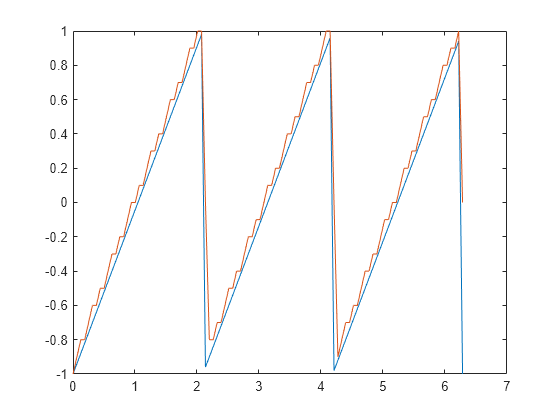

Figure contains an axes object. The axes object contains 2 objects of type line.

元の信号と復号化された信号の間の平均二乗誤差を計算します。

distor = sum((x-decodedx).^2)/length(x)
distor = 
0.0327

量子化のための DPCM パラメーターの最適化

ライブ スクリプトを開く

DPCM 符号化され、DPCM 復号化されたノコギリ波信号を最適化するには、dpcmopt関数を、dpcmenco関数およびdpcmdeco関数と共に使用します。大きな信号の集合に対し、微細な量子化方式を使用してパラメーターのテストや選択を行うのは手間のかかる作業です。分割、コードブック、および予測子のパラメーターを簡単に生成する方法の 1 つは、一連の "学習データ" に従ってそれらを最適化することです。学習データは、dpcmenco で量子化する典型的な種類の信号でなければなりません。

この例では、予測次数 1 を新しい最適化予測子の目的の次数として使用します。dpcmopt 関数は、ノコギリ波信号 x を学習データとして使用し、これらの最適化パラメーターを作成します。この例では、学習データ自体を量子化します。理論上、最適化パラメーターは、x と同様のその他のデータの量子化に適しています。最適化された DPCM の平均二乗歪みは、最適化されていない DPCM パラメーターによる歪みよりもはるかに小さくなります。

ノコギリ波信号と初期 DPCM パラメーターの変数を定義します。

t = [0:pi/50:2*pi];
x = sawtooth(3*t);
partition = [-1:.1:.9];
codebook = [-1:.1:1];
predictor = [0 1];      % y(k)=x(k-1)

dpcmopt 関数と初期コードブックおよび次数 1 を使用して、分割、コードブック、および予測子のベクトルを最適化します。次に、初期および最適化後の分割ベクトルとコードブック ベクトルを使用して、DPCM 符号化された信号を生成します。

[predictorOpt,codebookOpt,partitionOpt] = dpcmopt(x,1,codebook);
encodedx = dpcmenco(x,codebook,partition,predictor);
encodedxOpt = dpcmenco(x,codebookOpt,partitionOpt,predictorOpt);

DPCM 復号化を使用して、変調信号から x を復元します。元の信号と復号化され最適化された復号化信号の間の平均二乗誤差を計算します。

decodedx = dpcmdeco(encodedx,codebook,predictor);
decodedxOpt = dpcmdeco(encodedxOpt,codebookOpt,predictorOpt);
distor = sum((x-decodedx).^2)/length(x);
distorOpt = sum((x-decodedxOpt).^2)/length(x);

量子化の平均二乗歪みについて、初期の入力引数と最適化後の入力引数で比較します。

[distor, distorOpt]
ans = 1×2

    0.0327    0.0009

参考

関数

トピック