CORDIC ベースの QPSK 搬送波同期
このモデルでは、QPSK 搬送波同期に使用されるデジタル PLL (位相同期回路) 実装における CORDIC (COordinate Rotation DIgital Computer) 回転アルゴリズムの使い方について説明します。このモデルを実行するには Fixed-Point Designer™ が必要です。
はじめに
デジタル PLL の構造は連続時間 PLL の構造と本質的に等価です。PLL の構成要素は、位相誤差検出器 (PED)、ループ フィルター、および制御発振器です。
QPSK 搬送波 (位相と周波数) 同期の場合、デジタル P+I (比例プラス積分) フィルターとしてループ フィルターを実装すると、2 次 PLL が生成されます。制御発振器 (Phase Accumulator) は、受信した QPSK 信号の角度を複素回転を介して調整します。
複素回転は exp(j*theta) による直接複素数乗算など、さまざまな手法で実装できます。ただし、そのような実装はハードウェア (FPGA や ASIC など) リソースの観点からすると、比較的高コストになる可能性があります。代替手法としては、CORDIC ベースの回転アルゴリズムを使用して複素数乗算を実装します。この例では、この手法を使用します。これには、Fixed-Point Designer™ の関数 CORDICROTATE を使用します。これにより、乗数を抑えて複素回転近似値を得ることができますが、速度が犠牲になります。CORDIC を何回か反復するだけで良好なデジタル PLL 応答を達成できる場合も多く、本格的な複素数乗算を実装するためのハードウェア リソース コストは必要ありません。
例の構造
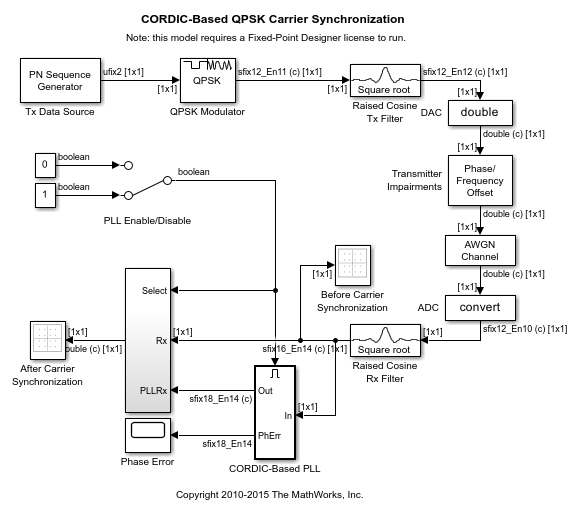

Tx データ ソース
Communications Toolbox™ の PN Sequence Generator ライブラリ ブロックは、Tx データ ソースであり、符号なし 2 ビット整数シンボルを生成します。
QPSK 変調器
Communications Toolbox の QPSK Modulator Baseband ライブラリ ブロックは、pi/4 位相オフセットとバイナリ コードのコンスタレーションを使用して、符号付き 12 ビット固定小数点変調器の出力値を計算します。
レイズド コサイン Tx フィルター
Communications Toolbox の Raised Cosine Transmit Filter ライブラリ ブロックは、アップサンプリング係数 8 で平方根 FIR フィルター処理を実行します。
送信機障害
Communications Toolbox の Phase/Frequency Offset ライブラリ ブロックは、関連する送信機障害をシミュレートします。Phase offset と Frequency offset の各パラメーター値を調整して、PLL Phase Error の時間スコープおよび受信信号散布図表示に及ぼす影響を確認できます。
AWGN チャネル
Communications Toolbox の AWGN Channel ライブラリ ブロックは、ノイズのあるチャネルをシミュレートします。ブロックの Eb/No パラメーターを調整して、PLL Phase Error の時間スコープおよび受信信号散布図表示に及ぼす影響を確認できます。
レイズド コサイン Rx フィルター
Communications Toolbox の Raised Cosine Receive Filter ライブラリ ブロックは、ダウンサンプリング係数 8 で平方根 FIR フィルター処理を実行します。
CORDIC-Based PLL サブシステム
CORDIC-Based PLL サブシステムは、Phase Error Detector (PED)、P+I Loop Filter、Phase Accumulator、および CORDICROTATE で構成され、訂正された複素信号出力値を形成します。
CORDIC ベース PLL

Phase Error Detector
Phase Error Detector は MATLAB® 関数を使用して実装されます。

P+I Loop Filter
P+I Loop Filter は 2 次 PLL を実装します。ループ定数 K1 (P ゲイン) と K2 (I ゲイン) は、マスクされた CORDIC-Based PLL サブシステムの Normalized loop bandwidth と Damping factor の各パラメーターから得られます。

Phase Accumulator
Phase Accumulator は角度 Theta を計算します。

CORDICROTATE
MATLAB 関数 CORDICROTATE は、乗数の少ない CORDIC ベースの反復アルゴリズムを使用して、複素受信信号を Theta で回転します。

結果と表示
Phase Error
Phase Error 時間スコープ ブロックを使用して、時変 PLL の Phase Error Detector の出力値を表示します。


Scatter Plots
Before Carrier Synchronization および After Carrier Synchronization のスコープ ブロックを使用して、Transmitter Impairments と AWGN Channel の各パラメーターを調整した結果を観察します。



例を試す
送信機障害
送信機位相と周波数オフセットの障害の影響を確認するには、モデルの実行中に Phase offset と Frequency offset の各パラメーター値を変更します。モデルの StopTime を inf に設定し、PLL Enable/Disable スイッチを使用して過渡応答の変化を観察します。
AWGN チャネル
ノイズのあるチャネルの影響を確認するには、モデルの実行中に Eb/No パラメーター値を変更します。モデルの StopTime を inf に設定し、PLL Enable/Disable スイッチを使用して過渡応答の変化を観察します。
CORDIC ベース PLL
PLL の Normalized loop bandwidth と Damping factor の各パラメーターを変更して、モデルの実行中に元になる P+I Loop Filter の動作を調整します。モデルの StopTime を inf に設定し、PLL Enable/Disable スイッチを使用して過渡応答の変化を観察します。
位相固定 QPSK 受信信号の出力には、位相不確定性が含まれることに注意してください。詳細な分析 (シンボル エラー レートの計算など) では、この位相不確定性は既知のトレーニング (プリアンブル) 信号、可変復調器位相オフセット、コンスタレーションの再配置など、よく知られている多くの方法のいずれかを使用して解決できる場合があります。
参考文献
Rice, Michael, "Discrete-Time Phase Locked Loops", Digital Communications: A Discrete-Time Approach, Appendix C, Sec. C.3, Pearson Prentice Hall, 2008.
Andraka, Ray, "A survey of CORDIC algorithm for FPGA based computers", Proceedings of the 1998 ACM/SIGDA Sixth International Symposium on Field Programmable Gate Arrays, 191 - 200, Feb. 22-24, 1998.
Volder, Jack E., "The CORDIC Trigonometric Computing Technique", IRE Transactions on Electronic Computers, Volume EC-8, 330 - 334, September 1959.