このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

超音速風洞に必要なコンプレッサー電力の計算

この例では、超音速風洞で必要なコンプレッサー電力を計算する方法を示します。

問題定義

このセクションでは解決すべき問題について説明します。必要な方程式と既知の値も提供します。

高度 20 キロメートルでのマッハ 2 の流れの動作条件をシミュレートするために、固定ジオメトリの超音速風洞を定常状態と起動時に実行するために必要なコンプレッサーの電力を計算します。

試験部は直径25センチメートルの円形です。テストセクションの後には固定面積の拡散器があります。風洞は、コンプレッサーによってシステムに追加される余分なエネルギーを排除するためにクーラーを使用します。したがって、コンプレッサー入口とテストセクションのよどみ点温度は同じになります。コンプレッサーは等エントロピーであり、摩擦の影響は無視できると仮定します。

steadyPicture = plotSupersonicWindTunnel('steady');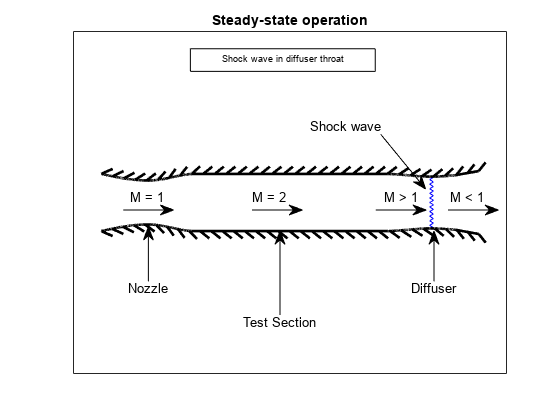

問題で与えられた情報は次のとおりです。

diameter = 25/100;  % Diameter of the cross-section [m]
height   = 20e+03;  % Design altitude [m]
testMach = 2.0;     % Mach number in the test section [dimensionless]

流体は空気であると仮定すると、次のような特性を持ちます。

k  = 1.4;       % Specific heat ratio [dimensionless]
cp = 1.004;     % Specific heat at constant pressure [kJ / (kg * K)]

直径から試験部の断面積が必要となります。

testSectionArea = pi * (diameter)^2 / 4 ; % [m^2]

設計高度は与えられているので、その高度での飛行条件を解きます。Aerospace Toolbox には、さまざまな高度での状態を計算するためのいくつかの機能があります。そのような関数の 1 つである atmosisa は、高度入力に基づいて、国際標準大気を使用して左側の飛行条件を計算します。

[testSectionTemp, testSectionSpeedOfSound, testSectionPressure, testSectionDensity] = atmosisa(height);

この関数は次の単位を使用します。

testSectionTemp = Static temperature in the test section        [K]
testSectionSpeedOfSound = Speed of sound in the test section    [m / s]
testSectionPressure = Static pressure in the test section       [kPa]
testSectionDensity = Density of the fluid in the test section   [kg / m^3]

停滞量の計算

テストセクションでは、停滞量 (合計) の多くを計算する必要があります。局所静的条件と停滞条件の比率は、flowisentropic で計算できます。

[~,tempRatioIsen, presRatioIsen, ~, areaRatioIsen] = flowisentropic(k, testMach);

左側の量はすべて無次元比です。ここで、静温度とよどみ温度の比を使用してよどみ温度を計算できます。

testSectionStagTemp = testSectionTemp / tempRatioIsen;

固定面積ディフューザーを備えた超音速風洞の定常動作に最適な条件は、ディフューザーのスロート部分に垂直衝撃波が存在するときに発生します。最適な状態を得るには、ディフューザーのスロートの面積をノズルのスロートの面積よりも小さくする必要があります。比熱が一定の完全気体であると仮定して、拡散器面積がノズル面積よりも小さくなければならない係数を計算します。この計算は、総圧力と断面積を含む質量保存の式を簡略化したものです。

$p_{t_{n o z z l e}} A_{n o z z l e}^{*} = p_{t_{d i f f u s e r}} A_{d i f f u s e r}^{*}$

ここで、

$p_{t_{n o z z l e}} = T o t a l p r e s s u r e a t t h e n o z z l e$

$p_{t_{d i f f u s e r}} = T o t a l p r e s s u r e a t t h e d i f f u s e r$

$A_{n o z z l e}^{*} = R e f e r e n c e a r e a f o r s o n i c f l o w a t t h e n o z z l e$

$A_{d i f f u s e r}^{*} = R e f e r e n c e a r e a f o r s o n i c f l o w a t t h e d i f f u s e r$

方程式を並べ替えます。

$\frac{A_{d i f f u s e r}^{*}}{A_{n o z z l e}^{*}} = \frac{p_{t_{n o z z l e}}}{p_{t_{d i f f u s e r}}}$

この例では、ノズルのスロート領域、テストセクション、および衝撃波の前のディフューザースロートにおける流れの領域が上流であると想定しています。衝撃波はディフューザーのスロートにあるため、ディフューザーのスロート領域は衝撃波の上流または下流のいずれかと考えることができます。この例では、ディフューザーのスロート領域が下流にあると想定しています。上流の流れは衝撃波までは等エントロピーなので、テストセクションのマッハ数を上流マッハ数として使用できます。これを行うと、衝撃を通る総圧力比を計算し、次にノズルとディフューザー領域間の面積比を計算できます。

総圧力比は次のとおりです。

$s t a g P r e s s R a t i o = \frac{p_{t_{d i f f u s e r}}}{p_{t_{n o z z l e}}}$

Aerospace Toolbox の法線衝撃関数を使用して総圧力比を計算します。

[~, ~, ~, ~, ~, stagPressRatio] = flownormalshock(k, testMach);

衝撃時の面積比は、

$a r e a R a t i o S h o c k = \frac{A_{n o z z l e}^{*}}{A_{d i f f u s e r}^{*}}$

前述のように質量保存則を用いると次の式が得られます。

areaRatioShock = stagPressRatio;

ディフューザーの面積を計算します。

diffuserArea = testSectionArea / (areaRatioShock * areaRatioIsen);

ディフューザーのスロート面積はテストセクション面積よりも小さいため、流れのマッハ数は 1 に収束する必要があります。面積比を入力として flowisentropic を使用して、衝撃波のすぐ上流のマッハ数を計算します。

diffuserMachUpstreamOfShock = flowisentropic(k, (1 / areaRatioShock), 'sup');

flownormalshock を使用して、衝撃波を通る流れの特性を計算します。ここでも、合計圧力比のみが必要であることに注意してください。

[~, ~, ~, ~, ~, P0] = flownormalshock(k, diffuserMachUpstreamOfShock);

定常状態の場合に必要な仕事と電力の計算

流体の単位質量あたりの圧縮機によって行われる仕事は、圧縮機を通るエンタルピーの変化に等しくなります。エンタルピーの定義から、一定圧力での流体の温度変化と比熱を知ることで、特定の仕事を計算します。

$s p e c i f i c W o r k = h_{o u t} - h_{i n} = c_{p} (T_{o u t} - T_{i n})$

等エントロピー圧縮機の場合、

$\frac{T_{o u t}}{T_{i n}} = {(\frac{p_{o u t}}{p_{i n}})}^{\frac{k - 1}{k}}$

上記の式を変形して温度差を求めます。コンプレッサーに入る温度はテストセクションのよどみ点温度と同じであることを思い出してください。

$T_{o u t} - T_{i n} = T_{i n} [{(\frac{p_{o u t}}{p_{i n}})}^{\frac{k - 1}{k}} - 1]$

tempDiff = testSectionStagTemp * ((1 / P0)^((k - 1) / k) - 1); % [K]

具体的な作業が見つかります。

specificWork = cp * tempDiff; % [kJ / kg]

必要な電力は、特定の仕事と質量流量の積に等しくなります。定常動作中、テストセクションを通過する質量流量は次のように表されます。

$m_{}^{˙} = ρ A V = ρ A M a$

ここで、すべての流量はテストセクション内の値です。

$m_{}^{˙} = M a s s f l o w r a t e$

$ρ = D e n s i t y$

$A = C r o s s - s e c t i o n a l a r e a o f t e s t s e c t i o n$

$V = V e l o c i t y$

$M = M a c h n u m b e r$

$a = L o c a l s p e e d o f s o u n d$

massFlowRate = testSectionDensity * testSectionArea * testMach * testSectionSpeedOfSound; % [kg / s]

最後に、定常動作中にコンプレッサーに必要な電力を計算します。

powerSteadyState = specificWork * massFlowRate;  % [kW]

起動時に必要な作業と電力の計算

startupPicture = plotSupersonicWindTunnel('startup');

起動条件では、衝撃波はテストセクション内にあります。衝撃波直前のマッハ数が試験区間マッハ数となります。

[~, ~, ~, ~, ~, stagPressRatioStartup] = flownormalshock(k, testMach);

ここで、等エントロピー圧縮機の特定の仕事を計算します。

specificWorkStartup = cp * testSectionStagTemp * ((1 / stagPressRatioStartup)^((k - 1) / k) - 1); % [kJ / kg]

次に、起動時に必要な電力を計算します。

powerStartup = specificWorkStartup * massFlowRate;   % [kW]

定常運転時に必要な電力 (53.1 kW) は、コンプレッサーの起動時に必要な電力 (97.9 kW) よりもはるかに低くなります。これらの必要な電力の結果は、それぞれ最適な動作条件と最悪の動作条件を表しています。

power = [powerSteadyState powerStartup];
barGraph = figure('name','barGraph');
bar(power,0.1);
ylabel('Power required [kilowatts]')
set(gca,'XTickLabel',{'powerSteadyState', 'powerStartup'})

リファレンス

[1] James, J. E. A.、「ガスダイナミクス、第2版」、Allyn and Bacon社、ボストン、1984年。

参考

atmosisa | flowfanno | flowisentropic | flownormalshock | flowprandtlmeyer