このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。

超音速ノズルの出口流れを解く

ライブスクリプトを開く

この例では、特性法とプラントル・マイヤー流れ理論を使用して、膨張を伴う超音速流れの問題を解決する方法を示します。超音速ノズルの出口の下流の流れ場を解きます。

問題定義

このセクションでは解決すべき問題について説明します。必要な方程式と既知の値も提供します。

特性法を使用して超音速ノズルの下流の流れ場を解きます。出口面のマッハ数は1.5、出口面の圧力は200キロパスカルです。背圧は100キロパスカルです。

前提:

流れは等エントロピーです。
流れ特性の変化は、ノズルの後流全体で発生する膨張波の相互作用によって決まります。
ノズルと流れの形状は対称です。

膨張ファンを 3 つの特性としてモデル化します。対称性のため、フローの上部半分のみで作業するように任意に選択します。以下はノズル出口の図です。

upperNozzle = plotExpansionSchematic('uppernozzle');

問題で与えられた情報は次のとおりです。

exitMach = 1.5; % Mach number at the exit plane [dimensionless]
exitPres = 200; % Static pressure at the exit plane [kPa]
backPres = 100; % Pressure downstream of the nozzle, outside of the expansion wake

流体は、次の一定の比熱比を持つ完全気体のように動作する空気であると仮定します。

k = 1.4; % Specific heat ratio [dimensionless]

特性法

特性法は、非回転ポテンシャル流れ方程式を完全非線形形式で解析する超音速流れの理論です。等エントロピー流れが想定されます。特性曲線の定義は、速度は連続しているが、速度の一次導関数は不連続である流れの曲線です。

前の図の青い線はおおよその特性です。タイプ I の特徴は、流れの方向に対して負の鋭角を形成することです。タイプ II の特徴は、流れの方向に対して正の鋭角を形成することです。この方法の詳細な導出は、この例の分析の範囲外です。この例の分析では、リージョン間手順を使用します。この手順については既に理解していることを前提としています。

プラントル・マイヤー流れと特性曲線法では、流れのすべての領域における重要な角度を計算します。

流れの角度は空気が移動する方向です。

$θ_{n} = F l o w a n g l e i n t h e n^{t h} r e g i o n$

プラントル・マイヤー角は、流れがある領域から別の領域へ方向を変える角度です。

$ν_{n} = P r a n d t l - M e y e r a n g l e i n t h e n^{t h} r e g i o n$

マッハ角は、局所的な流れの方向と特定の点から発生する弱い圧力波との間の角度です。

$μ_{n} = M a c h a n g l e i n t h e n^{t h} r e g i o n$

各領域のマッハ数を計算し、すべての領域の両方の特性の角度を解きます。すべての特性の傾斜と特性の交差点の位置を計算して、すべての領域の幾何学的境界を解きます。

第一膨張ファンを通る流れ特性の計算

後流外側のマッハ数（領域 4）を決定します。この場所のマッハ数は、圧力の等エントロピー比と圧力の指定された値を使用して見つけることができます。出口面での圧力比は、flowisentropic を使用して簡単に解くことができます。

[~, ~, exitPresRatio] = flowisentropic(k, exitMach);

背圧比は、背圧とよどみ点圧力の比です。外側の後流領域における等エントロピー圧力比は、次のとおりです。

$\frac{p_{4}}{p_{0}} = \frac{p_{4}}{p_{1}} \frac{p_{1}}{p_{0}}$

backPresRatio = backPres / exitPres * exitPresRatio;

flowisentropic を使用して領域 4 のマッハ数を計算します。

backMach = flowisentropic(k, backPresRatio, 'pres');

「pres」文字列入力は、関数が圧力比入力モードであることを示します。背圧領域の流れ角度は、出口平面領域 (領域 1) から背圧領域 (領域 4) までのプラントルマイヤー角の差です。

$θ_{4} = ν_{4} - ν_{1}$

[~, nu_1]    = flowprandtlmeyer(k, exitMach);
[~, nu_4]    = flowprandtlmeyer(k, backMach);
theta_4 = nu_4 - nu_1;

3 つの特性を持つ流れを近似するため、領域 1 から領域 4 までの交差タイプ I 特性における流れ角度の変化を計算します。

$Δ θ_{I} = \frac{θ_{4}}{3}$

deltaThetaI = theta_4 / 3;

領域 1 の流れは水平方向に平行であるため、次のことに注意してください。

theta_1 = 0;

実際、中心線をまたぐどの領域でも流れは中心線と平行です。これは、中心線がこの対称フローの境界であると考えられるためです。さらに、境界にはソースもシンクもありません。

theta_5  = 0;
theta_8  = 0;
theta_10 = 0;

領域 2 と 3 の流れ角度は単純です。

theta_2 = theta_1 + deltaThetaI;
theta_3 = theta_2 + deltaThetaI;

タイプ I 特性全体で、プラントル・マイヤー角の変化は流れ角の変化に等しくなります。

$Δ ν_{I} = Δ θ_{I}$

deltaNuI = deltaThetaI;

領域 1 の Prandtl-Meyer 角と、タイプ I 特性による Prandtl-Meyer 角の変化 deltaNuI を使用して、領域 2 の Prandtl-Meyer 角を計算します。領域 2 と同様の方法で、領域 3 のプラントルマイヤー角を計算します。

$Δ ν_{I} = ν_{2} - ν_{1}$

$ν_{2} = ν_{1} + Δ ν_{I}$

nu_2 = nu_1 + deltaNuI;
nu_3 = nu_2 + deltaNuI;

干渉領域における流れ特性の計算

中心線境界条件から、領域 5 の流れ角度はゼロであることがわかっています。したがって、領域2から領域5への角度の変化は

$Δ θ_{I I} = θ_{5} - θ_{2}$

deltaThetaII = theta_5 - theta_2;

タイプ II 特性全体にわたるプラントル・マイヤー角の変化を計算します。

$Δ ν_{I I} = - Δ θ_{I I}$

deltaNuII = -deltaThetaII;

次に、領域 5 の Prandtl-Meyer 角を計算します。領域 2 の Prandtl-Meyer 角と、タイプ II 特性全体にわたる Prandtl-Meyer 角の変化についてはすでにご存知でしょう。

nu_5 = nu_2 + deltaNuII;

領域 6 のプロパティを計算するには、領域 3 と領域 5 のプロパティが既知であるという事実を使用します。また、フローがどの特性を通過するかによってプロパティの変化が定義されることにも注意してください。領域 5 から領域 6 にかけて、タイプ I 特性が交差します。したがって次のようになります。

$Δ θ_{I} = Δ ν_{I} = θ_{6} - θ_{5} = ν_{6} - ν_{5}$

これを次のように並べ替えます。

$ν_{6} - θ_{6} = ν_{5} - θ_{5} (1)$

タイプ II 特性は、領域 3 から領域 6 に移動するときに交差します。したがって次のようになります。

$Δ ν_{I I} = - Δ θ_{I I}$

$ν_{6} - ν_{3} = θ_{3} - θ_{6}$

これを次のように並べ替えます。

$ν_{6} + θ_{6} = ν_{3} + θ_{3} (2)$

式(1)と式(2)を足し合わせて、領域6のプラントル・マイヤー角を解きます。これにより、次の式が生成されます。

$ν_{6} = \frac{(ν_{5} - θ_{5}) + (ν_{3} + θ_{3})}{2}$

MATLAB ® では、以下を使用します。

nu_6 = ((nu_5 - theta_5) + (nu_3 + theta_3))/2;

式（１）から、領域６における流れ角は

theta_6 = nu_6 - (nu_5 - theta_5);

領域 7 では、タイプ 1 の特性が交差し、すべての情報が領域 6 で利用可能になります。

nu_7    = nu_6 + deltaNuI;
theta_7 = theta_6 + deltaThetaI;

領域 8 は中心線上にあり、その流れ角度はゼロです。領域 6 から領域 8 に移動するには、タイプ II 特性を交差する必要があります。したがって、領域 8 のプラントルマイヤー角は次のように計算されます。

nu_8 = nu_6 + deltaNuII;

領域 6 の場合と同様に、領域 9 の Prandtl-Meyer 角と流れ角を計算します。領域 8 は、タイプ I 特性の上流領域です。領域 7 は、タイプ II 特性の上流領域です。

nu_9    = ((nu_8 - theta_8) + (nu_7 + theta_7))/2;
theta_9 = nu_9 - (nu_8 - theta_8);

地域 10 は中心線上にあります。流れは平行なので、流れの角度はゼロです。領域 9 の Prandtl-Meyer 角とタイプ II 特性の交差を使用して、領域 10 の Prandtl-Meyer 角を計算します。

nu_10 = nu_9 + deltaNuII;

フローパラメータ結果の準備と表の作成

今後の計算では、流れの角度を 1 つのベクトルに結合し、プラントルマイヤー角を別のベクトルに結合します。

flowAngles         = [theta_1; theta_2; theta_3; theta_4; theta_5; theta_6; theta_7; theta_8; theta_9; theta_10];

prandtlMeyerAngles = [nu_1; nu_2; nu_3; nu_4; nu_5; nu_6; nu_7; nu_8; nu_9; nu_10];

prandtlMeyerAngles を入力として flowprandtlmeyer 関数を使用して、各領域のマッハ数とマッハ角を計算します。この関数の結果を使用して、タイプ I およびタイプ II の特性が各領域内の水平方向となす角度を見つけることができます。次に、これらの角度を使用して、x-y 平面の傾斜を計算できます。ここで、中心線は x 軸、ノズルの出口面は y 軸です。タイプ I 特性とタイプ II 特性のそれぞれの傾きは次のようになります。

${(\frac{d y}{d x})}_{I} = t a n (θ - μ)$

${(\frac{d y}{d x})}_{I I} = t a n (θ + μ)$

注意: 次の表のタイプ I とタイプ II の値は、傾斜ではなく、水平に対する角度です。

% Preallocation for speed
machNumbers = zeros(size(flowAngles));
machAngles  = zeros(size(flowAngles));

for i = 1:numel(flowAngles)
    [machNumbers(i), ~, machAngles(i)] = flowprandtlmeyer(k, prandtlMeyerAngles(i), 'nu');
end

typeOne = flowAngles - machAngles;
typeTwo = flowAngles + machAngles;

m = (1:numel(machNumbers)).';
disp(table(m,round(flowAngles,2),round(prandtlMeyerAngles,2),round(machNumbers,3),round(machAngles,2),round(typeOne,2),round(typeTwo,2),...
    'VariableNames',["Region","theta (Deg)","nu (Deg)","Mach","mu (Deg)","type I (Deg)","type II (Deg)"]))

    Region    theta (Deg)    nu (Deg)    Mach     mu (Deg)    type I (Deg)    type II (Deg)
    ______    ___________    ________    _____    ________    ____________    _____________

       1             0        11.91        1.5     41.81         -41.81           41.81    
       2          4.45        16.35       1.65     37.29         -32.85           41.74    
       3          8.89         20.8      1.803      33.7          -24.8           42.59    
       4         13.34        25.24      1.959     30.69         -17.35           44.03    
       5             0         20.8      1.803      33.7          -33.7            33.7    
       6          4.45        25.24      1.959     30.69         -26.25           35.14    
       7          8.89        29.69      2.122     28.11         -19.22              37    
       8             0        29.69      2.122     28.11         -28.11           28.11    
       9          4.45        34.14      2.294     25.84          -21.4           30.29    
      10             0        38.58      2.477     23.81         -23.81           23.81

次の点に注意してください。

流れの角度は中心線から離れるにつれて大きくなります。
プラントル・マイヤー角は流れが下流に移動するにつれて増加します。
流れが下流に移動するにつれてマッハ数も増加します。

流れの幾何学を解く

流れの特性はすべての領域で既知ですが、流れ場を解くには、各領域の実際の形状を計算する必要があります。上記の表の最後の 2 つの列には、各特性タイプが水平方向に対してなす角度が含まれています。直線は各領域の流れの特性を近似するため、任意の 2 つの領域間の境界は、隣接する領域で各領域が作る角度の平均によって近似されます。波は膨張ファンを通って曲がるため、特性が発生するポイントから解析を開始します。特性はノズルのリップから始まり、下流に作用します。

中心線とノズルの出口面の交点が座標系の原点であると仮定します。また、長さはノズルの出口高さの半分に正規化されていると想定します。正の x- 軸は、下流方向の中心線に沿って水平に取られます。正の y 軸は、ノズルの出口面において垂直上向きになります。ノズルのリップは点(0,1)にあります。

上唇から伝播する 3 つの特性はすべてタイプ I 特性です。最も急な波が中心線と交差するまで、どの波も最も急な波に干渉しないため、最初に最も急な傾斜特性を分析します。対称ハーフノズルモデルでは、最も急な波がファンに反射し、膨張ファン内の他の波と干渉します。

中心線から「反射」するこの波は、実際には下端から伝播する最も急勾配のタイプ II 特性です。ただし、解析では対称性のため中心線が境界であるとみなされます。これにより、ノズルの両半分を操作した場合と同じ結果が得られます。

縁からの最も急な傾斜線は、領域 1 と領域 2 を分けるタイプ I 特性です。最も急な傾斜の波が水平となす角度を計算するには、タイプ I 特性が各領域でなす角度の平均を使用します。傾斜を計算するには三角法を使います。

avgAngle12 = (typeOne(1) + typeOne(2)) / 2;
slope12    = tand(avgAngle12);

以下の情報が判明しています:

x-y 空間における最初のタイプ I 波の傾き。
波の y 切片 (縁では y = 1)。
波は干渉なく中心線 (y = 0) と交差します。

傾きと切片の形をした直線の方程式を使用して、点の x 位置を計算します。x の位置の y = m*x+b を y = 0 と並べ替えて x = -b / m を作成します。これは、最初の下流ポイントであるポイント 1 の x の場所です。

y1 = 0; % On the centerline
x1 = -1 / slope12;

ポイント 1 から、最初のタイプ II 特性が伝播し、ファンに干渉します。ノズルリップから発生するその他のタイプ I 特性は、タイプ II 波によって乱されますが、その波に到達する前に乱されることはありません。したがって、最も急峻なタイプ II 特性とリップからのより平坦なタイプ I 波の交点を計算します。中心線から上方に伸びるタイプ II 特性は、領域 2 と領域 5 を分離します。2 つの角度の平均と関連する傾斜は次のように求められます。

avgAngle25 = (typeTwo(2) + typeTwo(5)) / 2;
slope25    = tand(avgAngle25);

2 番目に急峻なタイプ I 特性は、領域 2 と領域 3 を分離するノズルリップからのものです。水平との平均角度とそれに伴う波の傾斜は次のように表されます。

avgAngle23 = (typeOne(2) + typeOne(3)) / 2;
slope23    = tand(avgAngle23);

領域 2-3 境界と領域 2-5 境界の交点を計算します。この点が必要なのは、この時点で特性が互いに干渉するためです。両方の境界の傾きと各線上の点は既知です。ポイント 1 とノズルリップ (参照ポイント 0 になる) は既知です。交差点の未知の x 座標を解きます。2 本の線のいずれかの方程式でその x 位置を使用して、交差点の y 位置を見つけます。点 p を通り、傾き m を持つ直線の点-傾き形式方程式は次のようになります。

$y - y_{p} = m (x - x_{p})$

この形式の線の利点は、線を完全に定義するために必要なのは 1 つの点と傾斜だけであることです。下付き文字のない x と y は、線上の任意の点になります。ただし、2 本の線の交点は一意である必要があります。この交点を点2と呼ぶと、両直線の方程式は次のようになります。

$y_{2} - y_{0} = m_{2, 3} (x_{2} - x_{0}) (3)$

$y_{2} - y_{1} = m_{2, 5} (x_{2} - x_{1}) (4)$

ここで、

$m_{i, j} = S l o p e o f t h e b o u n d a r y b e t w e e n r e g i o n i a n d r e g i o n j$

引き算して並べ替えます:

$x_{2} = \frac{x_{1} m_{2, 5} - x_{0} m_{2, 3} + y_{0} - y_{1}}{m_{2, 5} - m_{2, 3}}$

軸の切片による値の一部を正確に知ることで、この式は次のように簡略化されます。

x2 = (x1 * slope25 + 1) / (slope25 -slope23);

以下の点2のy位置は、点2のx位置を上記の式(4)に代入することによって求められますが、式(3)に代入しても同様の結果が得られます。

y2 = (x2 - x1) * slope25;

傾きと切片の式と上記の手順を使用して、すべてのポイントを計算します。フロー内の 3 番目のポイントを計算するには、まず領域 3-4 境界と 3-6 境界の交点を計算します。境界線の角度は、水平との角度の平均を使用して計算されます。次に、三角法を使用して傾斜を見つけることができます。傾斜は 1 つのステップで計算されます。

slope34 = tand( (typeOne(3) + typeOne(4)) / 2 );
slope36 = tand( (typeTwo(3) + typeTwo(6)) / 2 );

領域 3 と領域 4 の境界はタイプ I 特性であり、領域 3 と領域 6 の境界はタイプ II 特性であるため、適切なタイプの角度を取るように注意してください。これらの境界線の点と傾斜の形式を互いに減算して、点 3 の x 位置を計算します。

x3 = (y2 - 1 - x2 * slope36) / (slope34 - slope36);
y3 = (x3 - x2) * slope36 + y2;

最初のタイプ II 特性はファンを超えて伝播し、他の特性に干渉しなくなります。最も急峻なタイプ II が伝播する方向を定義する角度は、領域 4 と 7 のタイプ II 波の平均となる角度です。

slope47 = tand( (typeTwo(4) + typeTwo(7)) / 2);

下流に進むには、2 番目に急なタイプ I 特性も解きます。点 2 の既知の位置から開始して、2 番目のタイプ I 特性の x 切片を計算します。ここでも、解法では直線の点と傾きの形式を使用します。ただし、中心線の境界に到達するまでは干渉は発生しません。「ポイント 4」の x 位置を見つけるには、1 本の線だけを考慮する必要があります。領域 5 と領域 6 の境界の傾斜はタイプ I 波です。

slope56 = tand( (typeOne(5) + typeOne(6)) / 2 );

再配置された点-傾斜形式 (中心線で y = 0 であることがわかっている) を使用して、点 4 を見つけます。

x4 = ( slope56 * x2 - y2 ) / slope56;
y4 = 0;

ポイント 2 と同じ方法でポイント 5 を計算します。領域 6-7 境界はタイプ I であり、領域 6-8 境界はタイプ II です。

slope67 = tand( ( typeOne(6) + typeOne(7)) / 2);
slope68 = tand( (typeTwo(6) + typeTwo(8)) / 2);

領域 6-7 境界上の既知のポイントはポイント 3 です。領域 6-8 境界上の既知のポイントはポイント 4 です。この情報を傾きと切片の形式で使用し、方程式を減算して並べ替えると、次の点の位置が得られます。

x5 = (-x4 * slope68 + x3 * slope67 + y4 -y3) / (slope67 - slope68);
y5 = (x5 - x4) * slope68 + y4;

2 番目のタイプ II 特性は、タイプ II 波の領域 7 の角度と領域 9 の角度の間の平均角度でファンを超えて伝播します。

slope79 = tand( (typeTwo(7) + typeTwo(9)) / 2);

最後に注目すべき点は、最も平坦なタイプ I 波の x 切片です。この点を計算するには、点 5 の位置を把握し、領域 8 と領域 9 の間のタイプ I 波の傾きを見つけます。

slope89 = tand( (typeOne(8) + typeOne(9)) / 2);
y6      = 0;
x6      = (slope89 * x5 - y5) / slope89;

最後のタイプ II 波は、領域 9 と領域 10 の間で平均化された角度で伝播します。

slope910 = tand( (typeTwo(9) + typeTwo(10)) /2);

すべての点が計算され、自由に伝播する線の傾きがわかったら、点を結びます。

points = plotExpansionSchematic('nozzlepoints');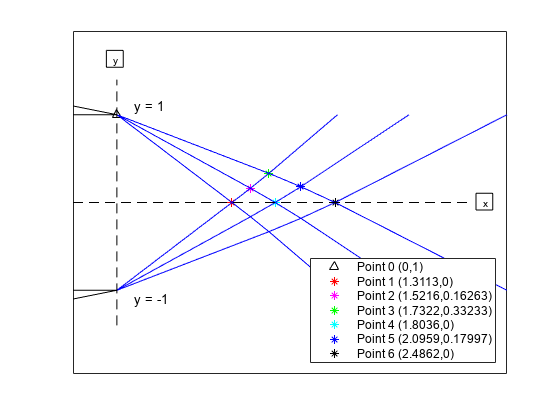

特性法は超音速気体力学の問題を解決するための強力な方法です。この方法は特性線の近似値を表すことに注意してください。この近似は、特性線の数が無限である場合の正確なケースに近づきます。

リファレンス

[1] James, J. E. A.、「ガスダイナミクス、第2版」、Allyn and Bacon社、ボストン、1984年。

参考

flowfanno | flowisentropic | flownormalshock | flowprandtlmeyer