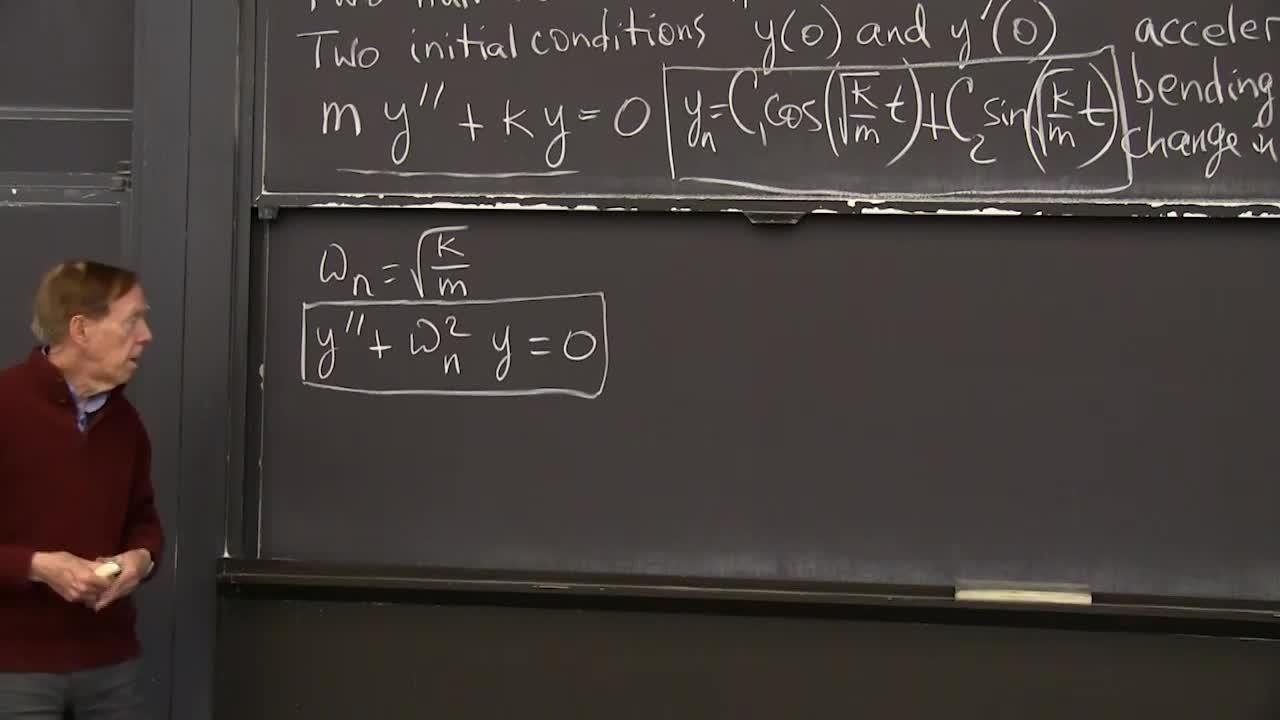Differential Equations and Linear Algebra, 2.1: Second Order Equations
From the series: Differential Equations and Linear Algebra
Gilbert Strang, Massachusetts Institute of Technology (MIT)
For the oscillation equation with no damping and no forcing, all solutions share the same natural frequency.
Published: 27 Jan 2016
OK, it's time to move on to second order equations. First order equations, we've done pretty carefully. Second order equations are a step harder. But they come up in nature, they come in every application, because they include an acceleration, a second derivative.
OK, so this would be a second order equation, because of that second derivative. I'm often going to have constant a, b, and c. We have enough difficulties to it without allowing those to change. So a, b, c constants, and doing the null solution to start with. Later, there'll be a forcing term on the right-hand side. But today, for this video, null solutions.
And the point is, now, what's new is that there are two null solutions. So y null will be a combination of e-- and they're both exponentials. Having constant coefficients there means exponentials in the solution. So e to the sum exponent, and another one to a, hopefully, different exponent. Sometimes if s1 equals s2, that'll be a special case and we'll have a slight change. But this is typical.
So we have two constants, c1 and c2, in the null solutions. And we need two initial conditions to determine those constants.
So previously, for a first order equation, we were given y of 0. Now, when we have acceleration, we give the initial velocity, y prime of 0. May I use prime as a shorthand for derivative? y prime of 0 is dydt, at 0.
So two condition will, at the right time, determine those two constants. And just to say again, so second derivative will be y double prime. And that represents, in physics, it represents acceleration-- change in velocity, change in y prime, is y double prime.
And in a graph of a function, y double prime shows up in bending of the graph. Because bending is a change in slope. Bending is a change in the slope. And the slope is y prime, the first derivative. So to measure changes in y prime, which will bend the graph, my chalk would be a tangent line. But if that changes, that gives us a y double prime, a second derivative.
OK, so I'm ready for some examples. And the first example-- the most basic equation of motion in physics and engineering, I would say-- it's called harmonic motion. And b is 0, that's the key point. b is 0.
It's Newton's law. And so a will be the mass m. y double prime, second derivative. b is 0. Later, b will be a damping term, a friction term, a resistance term. But let's have that 0. So we're going to have perpetual motion, here. Plus the force-- so this is Newton's law. ma is f, f equal ma. The force is proportional-- with a minus sign, so it's going to come on this side as a plus-- proportional to y. There's the equation.
No y prime term. my double prime, plus ky equals 0. Starting from an initial position, and an initial velocity, it's like a spring going up and down, or a clock pendulum going back and forth. And we'll see it, so it's going to be-- well, we want to solve that equation.
So do we see solutions to that? So if m and k were 1, suppose m and k were 1. I'm looking for a second derivative plus the function is 0. Second derivative is minus the function. I immediately think of sine t, and cosine t. Sines and cosines, because the second derivative-- the first derivative of a sine is cosine. The second derivative is minus the sine. It gives us the minus sign here, the plus sign there, 0. So the special solutions here are y is-- this is the null. I'm finding the null solution. Is, let me call them c1 times a cosine.
And now I have to figure out the cosine of what? I want the cosine to satisfy, to be a null solution, satisfy my equation. Let me put it in. If there's a square root of k over mt.
And you have to see that if I take two derivatives of the cosine, that will produce minus the cosine, which I want. And because of that, the chain will bring out this square root twice. So it will bring out the factor k over m for y double prime. And that factor, k over m, the m's will cancel and I'll have the k that matches that k. It's a solution.
And the other solution is just like it. It's the sine. Sine of this square root of k over m, t. That's worth putting a box around. That's what I mean by free harmonic motion. Something is just oscillating. In rotation problems, something is just going around a circle at a constant speed.
And notice, these are not the same as those. Cosines are related to exponentials, but not identical. So I could write the answer this way, using cosine and sine. Or as you'll see, I can write the same formula using exponentials, complex exponentials. Everybody remembers the big formula that allows complex numbers in here is Euler's formula, that the exponential of i omega t is the cosine plus i times the sine of omega t. I'll write it again.
That's the solution. It's got two null solutions. They're independent. They're different. And we've got two constants. Because our equation is linear, we can safely multiply by any constant, and add solutions, and they stay solutions because we have a linear equation, and 0 on the right-hand side. Good.
Of course, we can't write this square root of k over m forever. Let me do what everybody does-- introduce omega. It's omega natural. The n here stands for the natural frequency, the frequency that that clock is going at. And that is the square root of k over m.
So our equation, we could rewrite that equation. Let me rewrite that equation to make it simple. I'll divide by m. No problem, to divide by m. So then I have y double prime, plus k over m, which is omega n squared, the natural frequency squared. y equals 0. Let's put a box around that one, because you couldn't be better than that.
The constant a is 1. The constant b is 0. The constant c is a known omega n squared, depending on the pendulum itself. OK, and the solutions then, I'll just copy this solution. y null is c1 cosine of omega nt. Of course, omega n is that square rood. And c2 sine of omega nt.
Oh, well, wait a minute. I can figure out what c1 and c2 are , coming from the initial conditions, right? The initial conditions, if I plug in t equals 0, then I want to get the answer y of 0. The known initial condition, the place the pendulum started swinging from, the place the spring, you pull the spring a distance y of 0. You let go.
At t equals 0, so I'm plugging in t equals 0, at t equals 0, that's 0. Forget the sine. This is 1. So I discover that c1 should be y of 0. Simple. c1 is y of 0. Because that gives me the right answer, at t equals 0.
And what about c2? Can I figure out c2? Well, that's going to involve the initial velocity, the derivative, at t equals 0. Because the derivative of the sine is the cosine, which equals 1 at t equals 0, the derivative of this is the sine, which is 0. So that when I'm looking at y prime, the derivative, I'm looking here at t equals 0. And I want y prime of 0.
But I don't just want y prime of 0. Do you see that that doesn't have the right derivative, at t equals 0? Because when I take the derivative and omega n-- that constant, you remember that constant-- the derivative of this will bring out an omega n. So I better have an omega n down here to cancel it. And now I've got it.
That tells me the motion, forever and ever. Energy is constant. Potential energy plus kinetic energy, I could speak about energy. But I won't. That motion continues forever, free harmonic motion. OK, it goes on and on. OK. And again, I could write this in terms of complex exponentials. But I'm pretty happy with that form. It's hard to beat that form.
OK, so what else to do here. First of all, we're going to have cosine omega t's for quite awhile. I better draw the graph of that simple, familiar function. And so here's a graph of cosine omega t. So here's t. Here's cosine of omega. Here's 0. Here's 2-- well, let me see what I get.
So I go cosine of omega, cosine of omega t is what I'm drawing, not cosine t. Cosine t would go 0 to 2 pi. But I have cosine of omega t. So cosine of omega t is what I want to graph. So it starts at 1, and it comes back. It drops, comes back up, comes back to 1. But what is this t final? The period, this t is the period of the oscillation. It's the time it takes for the swing to go up and back. And what is that? That would be-- so I'm graphing cosine of omega t, is what I'm graphing.
So omega t starts out at 0, where t is 0. And it goes up to-- so I want omega t, when I get here, this omega t should be 2 pi. Right? Then I've completed the cosine, one rotation around the circle, one movement of the pendulum back and forth, is in that picture now. OK, so omega t is 2 pi, right? Right.
The period is t. I think of omega as the circular frequency. Omega is in radians per second. That's the units. And units truly are important to keep track. Omega, this is omega, radians per second, when I multiply by the period, the t in seconds, I get 2 pi radians.
OK now, in engineers and in everyday use, there's another frequency called f, for frequency probably. OK, so you should know about f. And its frequency is in hertz. So f is measured in hertz, H-E-R-T-Z, named after the guy. Not the tomato ketchup guy, but-- oh, that's Heinz anyway. Sorry about that.
Hertz -- not the car, that's what I was trying to say, but the German guy who was involved, early, with this stuff. So what is f? f times t is 1. Instead of dealing with 2 pi, which count to radians, the 1 just counts complete loops, complete oscillations. So f compared to know omega, f is smaller by a factor 2 pi. So f times t is 1. f is 1 over t. Omega is 2 pi over t. So putting these together, all I'm saying is, omega is 2 pi times f.
So when we say we're getting 60 cycles-- so that's what I would measure tf in. f would be in cycles, is cycles per second. One cycle, 2 pi radians. This isn't big, heavy math. But it's more important than a lot of math, just to get these letters straight.
So there's capital T, the period, and two measures of frequency. One is omega in radians per second, and the other is f in full cycles per second. So one is 2 pi times the other. Good. OK. And we have this. OK.
I think we've got the key ideas here, then, for unforced motion, pure oscillation going on forever. And let me just write what I already mentioned. A different way to express yn would be with small c's, e to the i omega nt. And c2 e to the minus i omega nt.
All I'm saying is that this form, with exponentials, is entirely equivalent to this form, with cosine and sine. That's form allows me two constants, capital C1 and C2. This form allows me two constants, little one and c2. And from that, I have this. From this, I have this. So we really do have exponentials here. And the key message is that for pure oscillation, those exponentials are pure imaginary exponent, i omega nt.
OK, that's the best example, the simplest example, the first example. Thanks.