このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

Morse ウェーブレット

Morse ウェーブレットとは

一般化 Morse ウェーブレットは、厳密な解析ウェーブレットのファミリです。解析ウェーブレットは、そのフーリエ変換が正の実数軸上にのみサポートをもつ複素数値のウェーブレットです。これらは、振幅および周波数が時間とともに変化する変調信号の解析に役立ちます。また、局在化した不連続の解析にも役立ちます。一般化 Morse ウェーブレットに関する独創性に富んだ論文が Olhede と Walden による[1]です。Morse ウェーブレットの理論と変調信号の解析への応用をさらに発展させたのが、Lilly と Olhede による一連の論文[2]、[3]、および[4]です。Morse ウェーブレットとその性質に関する計算で効率的なアルゴリズムを開発したのが、Lilly [5]です。

一般化 Morse ウェーブレットのフーリエ変換は次のとおりです。

$${\Psi }_{P,\gamma }(\omega )=U(\omega )a_{P,\gamma }{\omega }^{\frac{P^2}{\gamma }}{e}^{-{\omega }^{\gamma }},$$

ここで、U(ω) は単位ステップ、$$a_{P,\gamma }$$ は正規化定数、P² は時間-帯域積で、$$\gamma$$ は Morse ウェーブレットの対称性の特性を表します。Morse ウェーブレットに関する文献の多くでは $$\beta$$ を使用しています。これは、時間-帯域積 $$P^2=\beta \gamma$$ ではなく、減衰またはコンパクト性のパラメーターと考えることができます。$$\beta$$ と $$\gamma$$ でパラメーター化された、フーリエ領域での Morse ウェーブレットの式は次のようになります。

$${\Psi }_{\beta ,\gamma }(\omega )=U(\omega )a_{\beta ,\gamma }{\omega }^{\beta }{e}^{-{\omega }^{\gamma }}.$$

Morse ウェーブレットのパラメーター表現の詳細については、[2]を参照してください。

Morse ウェーブレットの時間-帯域積および対称性のパラメーターを調整することで、異なる性質および動作をもつ解析ウェーブレットを得ることができます。Morse ウェーブレットの強みは、よく使用される多くの解析ウェーブレットが一般化 Morse ウェーブレットの特殊なケースであることです。たとえば、コーシーのウェーブレットは $$\gamma$$ = 1 であり、ベッセルのウェーブレットは $$\beta$$ = 8 および $$\gamma$$ = 0.25 で近似されます。一般化 Morse と解析 Morlet ウェーブレットを参照してください。

Morse ウェーブレット パラメーター

前述のように、Morse ウェーブレットには 対称性と時間-帯域積の 2 つのパラメーターがあります。これらはウェーブレットの形状を決定し、変換の動作に影響を与えます。Morse ウェーブレットのガンマ パラメーター $$\gamma$$ は、復調歪度により時間におけるウェーブレットの対称性を制御します[2]。時間-帯域積の平方根 P は、時間におけるウェーブレットの持続期間に比例します。便宜上、cwt および cwtfilterbank の Morse ウェーブレットは、時間-帯域積とガンマとしてパラメーター化されています。持続時間は、ピーク周波数において時間領域のウェーブレットの中心ウィンドウに何回の振動が収まるかを決定します。ピーク周波数は、$${\omega }_{\psi }={\left(\frac{P^2}{{\gamma }^2}\right)}^{\frac{1}{\gamma }}.$$ です。

Morse ウェーブレットの (復調) 歪度は、ガンマが 3 に等しい場合、0 です。Morse ウェーブレットは、ガンマが 3 に等しい場合、最小のハイゼンベルグ領域も持ちます。このため、cwt および cwtfilterbank では、これを既定値として使用しています。

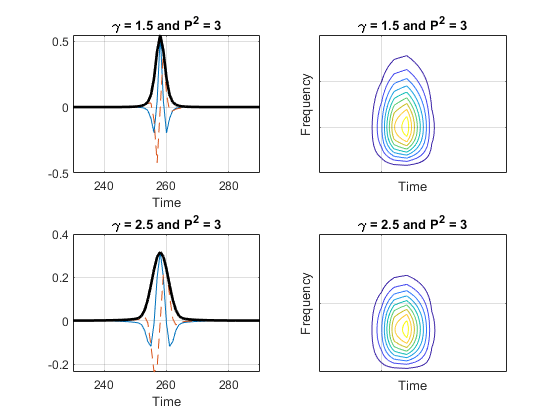
Morse ウェーブレットの形状に対するパラメーター値の効果

以下のプロットは、対称性と時間-帯域の値を変えると Morse ウェーブレットの形状にどのような影響があるかを示しています。時間-帯域が長いほど、ウェーブレットの中心部分が広がり、長期減衰率が増加します。対称性が増加すると、ウェーブレットの包絡線が広がりますが、長期減衰には影響しません。対称性の値が 3 以下の場合、時間-帯域が増加するにつれて時間減衰は増加します。対称性が 3 以上の場合、時間-帯域を減少すると、ウェーブレットの対称性は低下します。対称性と時間-帯域の両方が増加すると、ウェーブレットは時間において振動が多くなり、周波数は狭くなります。時間-帯域の値が非常に小さく、対称性の値が大きい場合、望ましくない時間領域のサイドローブや周波数領域の非対称性が生じます。

左の列にある時間領域のプロットでは、赤い線が実数部、青い線が虚数部です。右の列にある等高線図は、パラメーターが時間および周波数での広がりに与える影響を示しています。

解析 Morse ウェーブレットと解析信号の関係

実信号に対する解析ウェーブレットを使用したウェーブレット変換の係数は、対応する解析信号の係数に比例します。解析信号は、以下の逆フーリエ変換として定義されます。

$${\widehat{x}}_{a(\omega )}=\widehat{x}(\omega )+\text{sgn}(\omega )\widehat{x}(\omega )$$

解析信号の値は ω によって異なります。

• ω > 0 の場合、解析信号のフーリエ変換は、対応する非解析信号 $$\widehat{x}(\omega )$$ のフーリエ変換の 2 倍です。

• ω = 0 の場合、解析信号のフーリエ変換は、対応する非解析信号のフーリエ変換に等しくなります。

• ω < 0 の場合、解析信号のフーリエ変換は 0 になります。

$$Wf(u,s)$$ が、平行移動 u、スケール s における信号 f(t) のウェーブレット変換を示すとします。解析しているウェーブレットが解析的であれば、$$Wf(u,s)=\frac{1}{2}W{f}_a(u,s)$$ が得られます。ここで、f_a(t) は f(t) に対応する解析信号です。cwt で使用されるすべてのウェーブレットについて、各スケールでのピーク周波数におけるウェーブレット バンドパス フィルターの振幅は 2 に設定されています。さらに、cwt は L1 正規化を使用します。ラジアン周波数が ω₀ で振幅が A の実数値の正弦波入力では、解析ウェーブレットを使用したウェーブレット変換は、同じ周波数 ω₀ で振動し、振幅が $$\frac{A}{2}\widehat{\psi }(s{\omega }_0)$$ に等しい係数を生成します。スケール $$\frac{{\omega }_{\psi }}{{\omega }_0}$$ における係数を分離すると、ピーク振幅 2 によって、解析された振動成分が確実に適切な振幅 A となります。

解析ウェーブレット変換と解析信号係数の比較

この例では、実信号の解析ウェーブレット変換が、対応する解析信号の近似をどのように行うかを示します。

正弦波を使用して実証します。解析ウェーブレットを使用して正弦波のウェーブレット変換を求め、その正弦波の周波数に対応するスケールでウェーブレット係数を抽出すると、係数が解析信号を近似します。正弦波の場合、解析信号は同じ周波数の複素指数です。

周波数が 50 Hz の正弦波を作成します。

t = 0:.001:1;
x = cos(2*pi*50*t);

解析 Morse ウェーブレットを使用して連続ウェーブレット変換を求め、解析信号を求めます。hilbert を使用するには、Signal Processing Toolbox™ がなければなりません。

[wt,f] = cwt(x,1000,'voices',32,'ExtendSignal',false);
analytsig = hilbert(x);

正弦波の周波数 50 Hz に最も近いスケールでウェーブレット係数を求めます。

[~,idx] = min(abs(f-50));
morsecoefx = wt(idx,:);

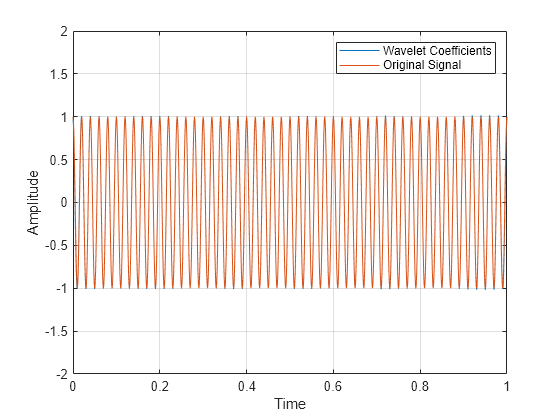
解析信号の実数部および虚数部を信号周波数におけるウェーブレット係数と比較します。

figure;
plot(t,[real(morsecoefx)' real(analytsig)']);
title('Real Parts'); 
ylim([-2 2]); grid on;
legend('Wavelet Coefficients','Analytic Signal','Location','SouthEast');
xlabel('Time'); ylabel('Amplitude');

figure;
plot(t,[imag(morsecoefx)' imag(analytsig)']);
title('Imaginary Parts'); 
ylim([-2 2]); grid on;
legend('Wavelet Coefficients','Analytic Signal','Location','SouthEast');
xlabel('Time'); ylabel('Amplitude');

cwt は、L1 正規化を使用し、ウェーブレット バンドパス フィルターのピーク振幅が 2 となるようにスケーリングします。上記の式における 1/2 の係数は、ピーク振幅の値によって相殺されます。

ウェーブレット変換は、信号の周波数局在型の信号のフィルター処理を表します。したがって、CWT 係数は、ヒルベルト変換係数よりもノイズに対する感度が高くありません。

信号にハイパス ノイズを付加し、ウェーブレット係数と解析信号を再度調査します。

y = x + filter(1,[1 0.9],0.1*randn(size(x)));
analytsig = hilbert(y);
[wt,f] = cwt(y,1000,'voices',32,'ExtendSignal',0);
morsecoefy = wt(idx,:);

figure;
plot(t,[real(analytsig)' x']);
legend('Analytic Signal','Original Signal');
grid on;
xlabel('Time'); ylabel('Amplitude');
ylim([-2 2])

figure;
plot(t,[real(morsecoefy)' x']);
legend('Wavelet Coefficients','Original Signal');
grid on;
xlabel('Time'); ylabel('Amplitude');
ylim([-2 2])

CWT に推奨する Morse ウェーブレットの設定

CWT を使用する場合、最適な結果を得るには、対称性 $$\gamma$$ として 3 を使用します。これは cwt および cwtfilterbank の既定値です。ガンマを固定して、時間-帯域積 $$P^2$$ を増加すると、周波数におけるウェーブレット フィルターが狭くなり、時間におけるフィルターの中心部分の幅が広くなります。また、フィルターの中心部分でのウェーブレットの振動回数が増加します。

参考文献

[1] Olhede, S. C., and A. T. Walden. “Generalized morse wavelets.” IEEE Transactions on Signal Processing, Vol. 50, No. 11, 2002, pp. 2661-2670.

[2] Lilly, J. M., and S. C. Olhede. “Higher-order properties of analytic wavelets.” IEEE Transactions on Signal Processing, Vol. 57, No. 1, 2009, pp. 146-160.

[3] Lilly, J. M., and S. C. Olhede. “On the analytic wavelet transform.” IEEE Transactions on Information Theory, Vol. 56, No. 8, 2010, pp. 4135–4156.

[4] Lilly, J. M., and S. C. Olhede. “Generalized Morse wavelets as a superfamily of analytic wavelets.” IEEE Transactions on Signal Processing Vol. 60, No. 11, 2012, pp. 6036-6041.

[5] Lilly, J. M. jLab: A data analysis package for MATLAB^®, version 1.6.2., 2016. http://www.jmlilly.net/jmlsoft.html.

[6] Lilly, J. M. “Element analysis: a wavelet-based method for analysing time-localized events in noisy time series.” Proceedings of the Royal Society A. Volume 473: 20160776, 2017, pp. 1–28. dx.doi.org/10.1098/rspa.2016.0776.