加速度計データからの亀裂の識別

この例では次を使用します。

この例では、ウェーブレットと深層学習の手法を使用して、舗装の横断亀裂を検出し、その位置を特定する方法を示します。この例では、ウェーブレット散乱シーケンスをゲート付き回帰ユニット (GRU) および 1 次元畳み込みネットワークへの入力として使用して、亀裂の有無に基づいて時系列を分類する方法を示します。データは助手席シート側のフロントホイールのサスペンションナックルに取り付けられたセンサーから取得した垂直加速度測定値です。舗装性能の評価と維持管理のためには、発生する横断亀裂を早期に特定することが重要です。信頼性の高い自動検出手法により、より頻繁で広範な監視が可能になります。

この例を実行する前に、データ - 説明および必要な属性をお読みください。データのインポートと前処理についてはすべて、データ — ダウンロードとインポートのセクションとデータ — 前処理のセクションで説明しています。学習テストセットの作成、前処理、特徴抽出、およびモデルの学習をスキップする場合は、分類と解析のセクションに直接進むことができます。前処理済みのテストデータ、抽出された特徴、学習済みのモデルをそこで読み込むことができます。

データ — 説明および必要な属性

この例で使用されているデータは、Mendeley Data オープンデータリポジトリ [2] から取得されました。データは Creative Commons (CC) BY 4.0 ライセンスの下で配布されます。この例で使用されるデータとモデルは、MATLAB® の tempdir コマンドで指定された一時ディレクトリにダウンロードします。tempdir とは異なるフォルダーにデータをダウンロードすることを選択した場合は、以降の手順でディレクトリ名を変更してください。TransverseCrackData として指定されたフォルダーにデータを解凍します。

dataURL = 'https://ssd.mathworks.com/supportfiles/wavelet/crackDetection/transverse_crack.zip';
saveFolder = fullfile(tempdir,'TransverseCrackData'); 
zipFile = fullfile(tempdir,'transverse_crack.zip');
websave(zipFile,dataURL);
unzip(zipFile,saveFolder)

データを解凍すると、TransverseCrackData フォルダーに transverse_crack_latest というサブフォルダーができます。以降のすべてのコマンドは、このフォルダーで実行しなければなりません。あるいは、このフォルダーを matlabpath に配置することもできます。

zip ファイル内のテキストファイル vehiclevibrationdata.rights には、CC BY 4.0 ライセンスのテキストが含まれています。データは元の Excel 形式から MAT ファイルに再パッケージ化されています。

データ収集については、[1] で詳しく説明されています。使用したのは、中央に配置された横断亀裂のあるアスファルトの長さ 4 メートルのセクション 12 個と、同じ長さの亀裂のないセクション 12 個です。データは 3 つの別々の道路から取得されます。横断亀裂の幅は 2 〜 13 mm で、亀裂の間隔は 7 〜 35 mm でした。セクションは次の 3 つの異なる速度で走行されました。30 km/hr、40 km/hr、および 50 km/hr。助手席側のサスペンションナックルからの垂直加速度測定値は、1.28 kHz のサンプリング周波数で取得されます。30、40、50 km/hr の各速度に対応するセンサー測定値は、30 km/hr では 6.5 mm、40 km/hr では 8.68 mm、50 km/hr では 10.85 mm ごとになります。この例の解析とは異なるこれらのデータの詳細なウェーブレット解析については、[1] を参照してください。

CC BY 4.0 ライセンスの規定に従い、この例で使用されているデータには元のデータの速度情報が保持されていないことに注意してください。速度と道路の情報は、完全性を期すために、データフォルダーに含まれる road1.mat、road2.mat、road3.mat データファイルに保持されます。

データ — ダウンロードとインポート

加速度計データとそれに対応するラベルを読み込みます。327 件の加速度計の記録があります。

load(fullfile(saveFolder,"transverse_crack_latest","allroadData.mat"))
load(fullfile(saveFolder,"transverse_crack_latest","allroadLabel.mat"))

データ — 前処理

すべての時系列の長さを取得します。長さごとに時系列の数の棒グラフを表示します。

tslen = cellfun(@length,allroadData);
uLen = unique(tslen);
Ng = histcounts(tslen);
Ng = Ng(Ng > 0);
bar(uLen,Ng,0.5)
grid on
AX = gca;
AX.YLim = [0 max(Ng)+15];
text(uLen(1),Ng(1)+10,num2str(Ng(1)))
text(uLen(2),Ng(2)+10,num2str(Ng(2)))
text(uLen(3),Ng(3)+10,num2str(Ng(3)))
xlabel('Length in Samples')
ylabel('Number of Series')
title('Time Series Length')

データセットには次の 3 つの一意の長さがあります。369、461、および 615 サンプル。車両は 3 つの異なる速度で走行していますが、移動距離とサンプルレートが一定であるため、データレコード長が異なります。"亀裂あり" (CR) クラスと "亀裂なし" (UNCR) クラスにあるレコードの数を判定します。

countlabels(allroadLabel)

ans=2×3 table
    Label    Count    Percent
    _____    _____    _______

    CR        109     33.333 
    UNCR      218     66.667

このデータセットは大幅に不均衡です。亀裂なし (UNCR) の時系列は、亀裂あり (CR) の時系列の 2 倍あります。これは、各レコードの "亀裂なし" を予測する分類器が、学習なしで 67% の精度を達成することを意味します。

時系列の長さも異なります。ウェーブレット散乱変換を使用するには、共通の入力長が必要です。再帰型ネットワークで、長さが異なる時系列を入力として使用することはできますが、ミニバッチ内のすべての時系列が、学習オプションに基づいてパディングまたは切り捨てられます。このため、学習とテストのミニバッチを作成する際には、パディングされたシーケンスが適切に分散されるように注意する必要があります。さらに、学習中にデータをシャッフルしないようにする必要があります。この小さなデータセットでは、各エポックの学習データをシャッフルするのが適切です。これにより、共通の時系列の長さが使用されます。

最も多い長さは 461 サンプルです。さらに亀裂は、それが存在する場合、記録内で中央に配置されます。したがって、最初と最後の 46 サンプルを反映することにより、369 サンプルの時系列を長さ 461 まで対称的に拡張できます。615 サンプルの記録では、最初の 77 サンプルと最後の 77 サンプルを削除します。

学習 — 特徴抽出とネットワーク学習

以下の節では、学習セットとテストセットを生成し、ウェーブレット散乱シーケンスを作成し、ゲート付き回帰ユニット (GRU) と 1 次元畳み込みネットワークの両方に学習させます。まず、両セット内の時系列について拡張または切り捨てを行い、461 サンプルの共通の長さを取得します。

allroadData = equalLenTS(allroadData);
all(cellfun(@numel,allroadData)== 461)

ans = logical
   1

亀裂ありのデータセットと亀裂なしのデータセット両方のそれぞれの時系列に、461 個のサンプルが存在することになります。各クラスの時系列の 80% で構成される学習セット用にデータを分割し、各クラスの残りの 20% をテスト用に保持します。各セットで比率が不均衡なままであることを確認します。

splt8020 = splitlabels(allroadLabel,0.80);
countlabels(allroadLabel(splt8020{1}))

ans=2×3 table
    Label    Count    Percent
    _____    _____    _______

    CR         87     33.333 
    UNCR      174     66.667

countlabels(allroadLabel(splt8020{2}))

ans=2×3 table
    Label    Count    Percent
    _____    _____    _______

    CR        22      33.333 
    UNCR      44      66.667

学習セットとテストセットを作成します。

TrainData = allroadData(splt8020{1});
TrainLabels = allroadLabel(splt8020{1});
TestData = allroadData(splt8020{2});
TestLabels = allroadLabel(splt8020{2});

学習の前に、データとラベルを 1 回シャッフルします。

idxS = randperm(length(TrainData));
TrainData = TrainData(idxS);
TrainLabels = TrainLabels(idxS);
idxS = randperm(length(TrainData));
TrainData = TrainData(idxS);
TrainLabels = TrainLabels(idxS);

各学習シリーズの散乱シーケンスを計算します。散乱シーケンスは、GRU ネットワークおよび 1 次元畳み込みネットワークと互換性をもつように cell 配列に格納されます。

XTrainSCAT = cell(size(TrainData));
for kk = 1:numel(TrainData)
    XTrainSCAT{kk} = helperscat(TrainData{kk});
end
npaths = cellfun(@(x)size(x,1),XTrainSCAT);
inputSize = npaths(1);

学習 — GRU ネットワーク

GRU ネットワーク層を作成します。それぞれ 30 の隠れユニットをもつ 2 つの GRU 層と、2 つのドロップアウト層を使用します。クラスが著しく不均衡であるため、クラスの重みをクラスの頻度の逆数に比例させた重み付き分類層を使用します。入力サイズは、散乱パスの数です。このネットワークに生の時系列で学習させるには、inputSize を 1 に変更し、各時系列を行ベクトル (1 行 461 列) に転置します。ネットワーク学習をスキップする場合は、分類と解析のセクションに直接進むことができます。学習済みの GRU ネットワーク、および前処理された学習セットとテストセットを、そこで読み込むことができます。

numHiddenUnits1 = 30;
numHiddenUnits2 = 30;
numClasses = 2;
classFrequencies = countcats(allroadLabel);
Nsamp = sum(classFrequencies);
weightCR = 1/classFrequencies(1)*Nsamp/2;
weightUNCR = 1/classFrequencies(2)*Nsamp/2;
GRUlayers = [ ...
    sequenceInputLayer(inputSize,'Name','InputLayer', ...
        'Normalization','zerocenter')
    gruLayer(numHiddenUnits1,'Name','GRU1','OutputMode','sequence')
    dropoutLayer(0.35,'Name','Dropout1')
    gruLayer(numHiddenUnits2,'Name','GRU2','OutputMode','last')
    dropoutLayer(0.2,'Name','Dropout2')
    fullyConnectedLayer(numClasses,'Name','FullyConnected')
    softmaxLayer('Name','smax');
    classificationLayer('Name','ClassificationLayer','Classes',["CR" "UNCR"], ...
        'ClassWeights',[weightCR weightUNCR]);
        ];

GRU ネットワークに学習させます。150 エポックの 15 のミニバッチサイズを使用します。

maxEpochs = 150;
miniBatchSize = 15;

options = trainingOptions('adam', ...
    'L2Regularization',1e-3, ...
    'MaxEpochs',maxEpochs, ...
    'MiniBatchSize',miniBatchSize, ...
    'Shuffle','every-epoch', ...
    'Verbose',0, ...
    'Plots','none');
iterPerEpoch = floor(length(XTrainSCAT)/miniBatchSize);
[scatGRUnet,infoGRU] = trainNetwork(XTrainSCAT,TrainLabels,GRUlayers,options);

平滑化された学習精度と反復ごとの損失をプロットします。

figure
subplot(2,1,1)
smoothedACC = filter(1/iterPerEpoch*ones(iterPerEpoch,1),1, ...
    infoGRU.TrainingAccuracy);
smoothedLoss = filter(1/iterPerEpoch*ones(iterPerEpoch,1),1, ...
    infoGRU.TrainingLoss);
plot(smoothedACC)
title(['Training Accuracy (Smoothed) ' ...
    num2str(iterPerEpoch) ' iterations per epoch'])
ylabel('Accuracy (%)')
ylim([0 100.1])
grid on
xlim([1 length(smoothedACC)])
subplot(2,1,2)
plot(smoothedLoss)
ylim([-0.01 1])
grid on
xlim([1 length(smoothedLoss)])
ylabel('Loss')
xlabel('Iteration')

分類用に、ホールドアウトされたテストデータのウェーブレット散乱変換を取得します。

XTestSCAT = cell(size(TestData));
for kk = 1:numel(TestData)
    XTestSCAT{kk} = helperscat(TestData{kk});
end

学習 — 1 次元畳み込みネットワーク

ウェーブレット散乱シーケンスを使用して 1 次元畳み込みネットワークに学習させます。ネットワーク学習をスキップする場合は、分類と解析のセクションに直接進むことができます。学習済みの畳み込みネットワーク、および前処理された学習セットとテストセットを、そこで読み込むことができます。

1 次元畳み込みネットワークを作成して学習させます。散乱ネットワークには 28 のパスがあります。

conv1dLayers = [
    sequenceInputLayer(28,'MinLength',58,'Normalization','zerocenter');
    convolution1dLayer(3,24,'Stride',2);
    batchNormalizationLayer;
    reluLayer;
    maxPooling1dLayer(4);
    convolution1dLayer(3,16,'Padding','same');
    batchNormalizationLayer;
    reluLayer;
    maxPooling1dLayer(2);
    fullyConnectedLayer(150);
    fullyConnectedLayer(2);
    globalAveragePooling1dLayer;
    softmaxLayer;
    classificationLayer('Name','ClassificationLayer','Classes',["CR","UNCR"], ...
    'ClassWeights',[weightCR weightUNCR]);
    ];

convoptions = trainingOptions('adam', ...
    'InitialLearnRate',0.01, ...
    'LearnRateSchedule','piecewise', ...
    'LearnRateDropFactor',0.5, ...
    'LearnRateDropPeriod',5, ...
    'Plots','none',...
    'MaxEpochs',50, ...
    'Verbose',0, ...
    'Plots','none', ...
    'MiniBatchSize',miniBatchSize);
[scatCONV1Dnet,infoCONV] = ...
    trainNetwork(XTrainSCAT,TrainLabels,conv1dLayers,convoptions);

平滑化された学習精度と反復ごとの損失をプロットします。

iterPerEpoch = floor(length(XTrainSCAT)/miniBatchSize);
figure
subplot(2,1,1)
smoothedACC = filter(1/iterPerEpoch*ones(iterPerEpoch,1),1, ...
    infoCONV.TrainingAccuracy);
smoothedLoss = filter(1/iterPerEpoch*ones(iterPerEpoch,1),1, ...
    infoCONV.TrainingLoss);
plot(smoothedACC)
title(['Training Accuracy (Smoothed) ' ...
    num2str(iterPerEpoch) ' iterations per epoch'])
ylabel('Accuracy (%)')
ylim([0 100.1])
grid on
xlim([1 length(smoothedACC)])
subplot(2,1,2)
plot(smoothedLoss)
ylim([-0.01 1])
grid on
xlim([1 length(smoothedLoss)])
ylabel('Loss')
xlabel('Iteration')

分類と解析

学習済みのゲート付き回帰ユニット (GRU) と 1 次元畳み込みネットワーク、およびテストデータと散乱シーケンスを読み込みます。すべてのデータ、特徴、およびネットワークは、学習 — 特徴抽出とネットワーク学習のセクションで作成したものです。

load(fullfile(saveFolder,"transverse_crack_latest","TestData.mat"))
load(fullfile(saveFolder,"transverse_crack_latest","TestLabels.mat"))
load(fullfile(saveFolder,"transverse_crack_latest","XTestSCAT.mat"))
load(fullfile(saveFolder,"transverse_crack_latest","scatGRUnet"))
load(fullfile(saveFolder,"transverse_crack_latest","scatCONV1Dnet.mat"))

学習データの前処理済みデータ、ラベル、およびウェーブレット散乱シーケンスがさらに必要な場合、次のコマンドを使用してそれらを読み込むことができます。以下の load コマンドをスキップした場合、これらのデータとラベルはこの例の残りの部分で使用されません。

load(fullfile(saveFolder,"transverse_crack_latest","TrainData.mat"))
load(fullfile(saveFolder,"transverse_crack_latest","TrainLabels.mat"))
load(fullfile(saveFolder,"transverse_crack_latest","XTrainSCAT.mat"))

テストセット内のクラスごとの時系列の数を調べます。データ — 前処理のセクションで説明したように、テストセットは大幅に不均衡であることに注意してください。

countlabels(TestLabels)

ans=2×3 table
    Label    Count    Percent
    _____    _____    _______

    CR        22      33.333 
    UNCR      44      66.667

XTestSCAT には、TestData の生の時系列に対して計算されたウェーブレット散乱シーケンスが格納されています。

モデル学習で使用されていないテストデータで、GRU モデルのパフォーマンスを表示します。

miniBatchSize = 15;
ypredSCAT = classify(scatGRUnet,XTestSCAT, ...
    'MiniBatchSize',miniBatchSize);
figure
confusionchart(TestLabels,ypredSCAT,'RowSummary','row-normalized', ...
    'ColumnSummary','column-normalized')
title({'GRU network -- Wavelet Scattering Sequences'; ...
    'Confusion chart with precision and recall'})

クラス内の不均衡が大きく、データセットが小さいにもかかわらず、適合率と再現率の値は、テストデータに対してネットワークが十分なパフォーマンスを発揮していることを示しています。具体的には、"亀裂あり" のデータの適合率と再現率の値が優れています。これは、学習セットのレコードの 67% が "亀裂なし" であるという事実にもかかわらず達成されます。ネットワークは不均衡ではありますが、時系列を "亀裂なし" として分類することにおいて過剰学習とはなっていません。

inputSize = 1 に設定し、学習データの時系列を転置すれば、生の時系列データで GRU ネットワークを再学習できます。これは、学習セット内の同じデータに対して行います。そのネットワークを読み込み、テストセットのパフォーマンスをチェックできます。

load(fullfile(saveFolder,"transverse_crack_latest","tsGRUnet.mat"))
rawTest = cellfun(@transpose,TestData,'UniformOutput',false);
miniBatchSize = 15;
YPredraw = classify(tsGRUnet,rawTest, ...
    'MiniBatchSize',miniBatchSize);
confusionchart(TestLabels,YPredraw,'RowSummary','row-normalized', ...
    'ColumnSummary','column-normalized')
title({'GRU network -- Raw Time Series'; ...
    'Confusion chart with precision and recall'})

このネットワークの場合、パフォーマンスは良くありません。特に、"亀裂あり" データの再現率が低くなっています。"亀裂" データに関する偽陰性の数がかなり多くなっています。これは、モデルの学習が十分に行われていない場合に不均衡なデータセットで想定される結果とまったく同じです。

ウェーブレット散乱シーケンスで学習を行った 1 次元畳み込みネットワークをテストします。

miniBatchSize = 15;
YPredSCAT = classify(scatCONV1Dnet,XTestSCAT, ...
    'MiniBatchSize',miniBatchSize);
figure
confusionchart(TestLabels,YPredSCAT,'RowSummary','row-normalized', ...
    'ColumnSummary','column-normalized')
title({'1-D Convolutional Network-- Wavelet Scattering Sequences'; ...
    'Confusion chart with precision and recall'})

散乱シーケンスをもつ畳み込みネットワークのパフォーマンスは非常に良好であり、GRU ネットワークのパフォーマンスと一致しています。少数クラスの適合率と再現率は、ロバスト学習を実証しています。

生のシーケンスで 1 次元畳み込みネットワークに学習させるために、sequenceInpuLayer 内で inputSize を 1 に設定します。'MinLength' を 461 に設定します。同じデータと同じネットワークアーキテクチャを使用して学習させたネットワークを読み込んでテストできます。

load(fullfile(saveFolder,"transverse_crack_latest","tsCONV1Dnet.mat"))
miniBatchSize = 15;
TestDataT = cellfun(@transpose,TestData,'UniformOutput',false);
YPredRAW = classify(tsCONV1Dnet,TestDataT, ...
    'MiniBatchSize',miniBatchSize);
confusionchart(TestLabels,YPredRAW,'RowSummary','row-normalized', ...
    'ColumnSummary','column-normalized')
title({'1-D Convolutional Network-- Raw Sequences'; ...
    'Confusion chart with precision and recall'})

生のシーケンスを使用した 1 次元畳み込みネットワークのパフォーマンスは良好ですが、ウェーブレット散乱シーケンスを使用して学習させた畳み込みネットワークには及びません。

ウェーブレット推定とウェーブレット解析

この節では、事前学習済みのモデルでのウェーブレット解析を使用して、1 つの時系列を分類する方法を示します。使用されるモデルは、ウェーブレット散乱シーケンスで学習を行った 1 次元畳み込みネットワークです。学習済みのネットワークといくつかのテストデータを前節で読み込んでいない場合、それらを読み込みます。

load(fullfile(saveFolder,"transverse_crack_latest","scatCONV1Dnet.mat"))
load(fullfile(saveFolder,"transverse_crack_latest","TestData.mat"))

ウェーブレット散乱ネットワークを作成し、データを変換します。テストデータから時系列を選択し、データを分類します。モデルが時系列を "亀裂あり" として分類する場合、その系列で波形の亀裂の位置を調査します。

sf = waveletScattering('SignalLength',461, ...
    'OversamplingFactor',1,'qualityfactors',[8 1], ...
    'InvarianceScale',0.05,'Boundary','reflect','SamplingFrequency',1280);
idx = 22;
data = TestData{idx};
[smat,x] = featureVectors(data,sf);
PredictedClass = classify(scatCONV1Dnet,smat);
if isequal(PredictedClass,'CR') 
    fprintf('Crack detected. Computing wavelet transform modulus maxima.\n')
    wtmm(data,'Scaling','local')
end

Crack detected. Computing wavelet transform modulus maxima.

Figure contains an axes object and an object of type uitable. The axes object with title Wavelet Transform Maxima Lines contains 122 objects of type image, line.

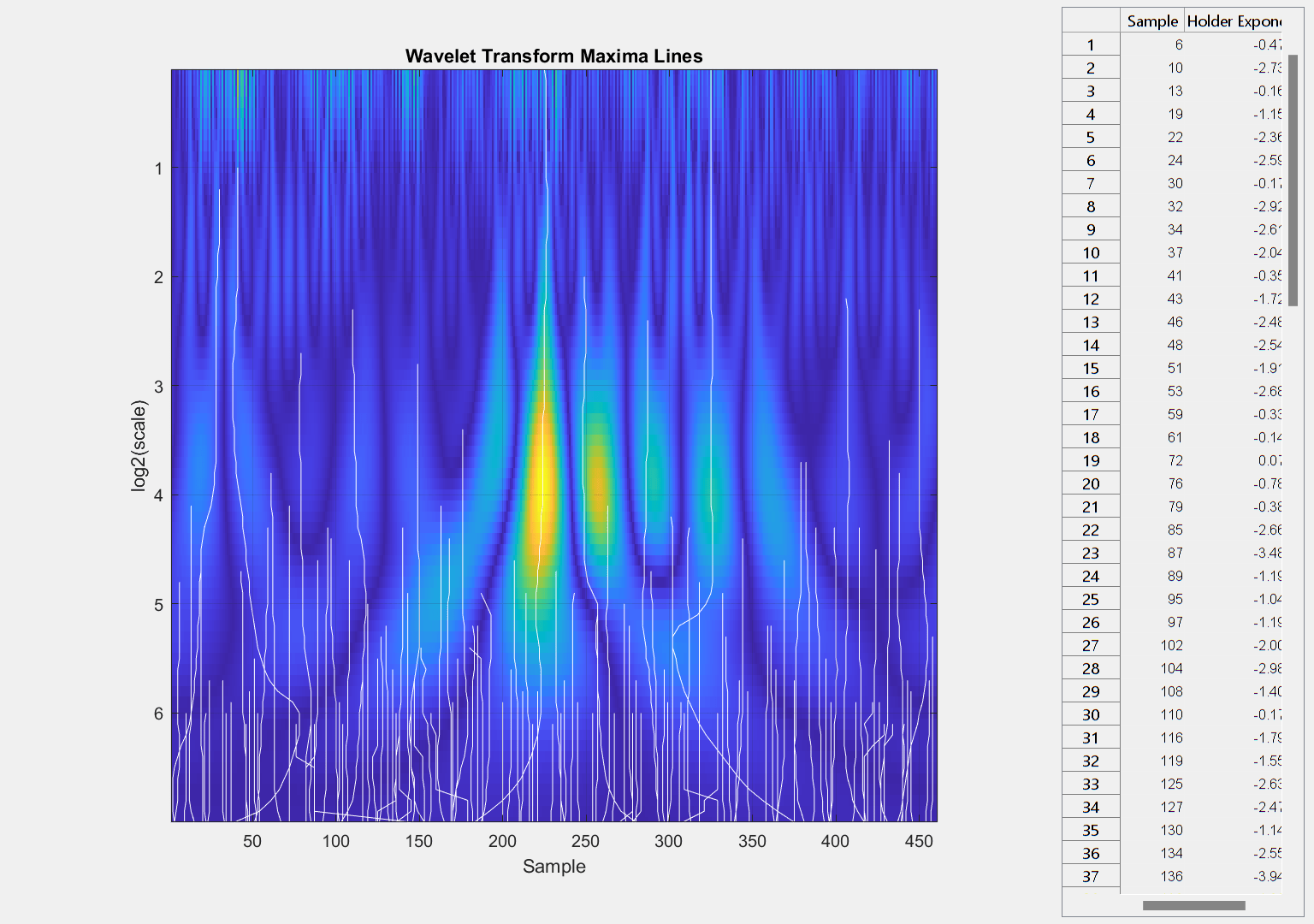
ウェーブレット変換係数最大値 (WTMM) 手法では、サンプル 225 で最も細かいスケールに収束する最大値ラインが示されます。細かいスケールに収束する最大値ラインは、特異点が時系列のどこにあるかに関する確度の高い推定値です。サンプル 225 は、亀裂の位置に関する確度の高い推定値になります。

figure
plot(x,data)
axis tight
hold on
plot([x(225) x(225)],[min(data) max(data)],'k')
hold off
grid on
title(['Crack located at ' num2str(x(225)) ' meters'])
xlabel('Distance (m)')
ylabel('Amplitude')

多重解像度解析 (MRA) 手法を使用し、大きいスケールのウェーブレット MRA 系列における勾配の変化を識別することにより、この位置の信頼度を高めることができます。MRA 手法の概要については、Practical Introduction to Multiresolution Analysisを参照してください。[1] において、"亀裂あり" 系列と "亀裂なし" 系列の間のエネルギーの差は、低い周波数帯域、特に [10,20] Hz の区間で発生しています。このため、次の MRA は、[10,80] Hz からの周波数帯域における信号成分に焦点を当てています。これらの帯域で、データの線形変化を識別します。MRA 成分と共に変化点をプロットします。

[mra,chngpts] = helperMRA(data,x);

MRA ベースの変更点解析は、亀裂と考えられる位置として約 1.94 メートルの領域を識別する際に WTMM 解析を確認するのに役立っています。

まとめ

この例では、再帰ネットワークと畳み込みネットワークの両方でウェーブレット散乱シーケンスを使用し、時系列を分類する方法を示しました。この例では、さらに、ウェーブレット手法が元のデータと同じ空間 (時間) スケールで特徴を位置推定するのにどう役立つかを実証しました。

参考文献

[1] Yang, Qun and Shishi Zhou. "Identification of asphalt pavement transverse cracking based on vehicle vibration signal analysis.", Road Materials and Pavement Design, 2020, 1-19. https://doi.org/10.1080/14680629.2020.1714699.

[2] Zhou,Shishi. "Vehicle vibration data." https://data.mendeley.com/datasets/3dvpjy4m22/1. データは CC BY 4.0 で使用しました。データは元の Excel データ形式から MAT ファイルに再パッケージ化しました。Speed ラベルは削除し、"crack" ラベルまたは "nocrack" ラベルのみを保持しました。

付録

この例では、補助関数を使用します。

function smat = helperscat(datain)
% This helper function is only in support of Wavelet Toolbox examples.
% It may change or be removed in a future release.
datain = single(datain);

sn = waveletScattering('SignalLength',length(datain), ...
    'OversamplingFactor',1,'qualityfactors',[8 1], ...
    'InvarianceScale',0.05,'Boundary','reflect','SamplingFrequency',1280);
smat = sn.featureMatrix(datain);

end

%-----------------------------------------------------------------------
function dataUL = equalLenTS(data)
% This function in only in support of Wavelet Toolbox examples.
% It may change or be removed in a future release.
N = length(data);
dataUL = cell(N,1);
for kk = 1:N
    L = length(data{kk});
    switch L
        case 461
            dataUL{kk} = data{kk};
        case 369
            Ndiff = 461-369;
            pad = Ndiff/2;
            dataUL{kk} = [flip(data{kk}(1:pad)); data{kk} ; ...
                flip(data{kk}(L-pad+1:L))];     
        otherwise
            Ndiff = L-461;
            zrs = Ndiff/2;
            dataUL{kk} = data{kk}(zrs:end-zrs-1);
    end
end       

end

%--------------------------------------------------------------------------
function [fmat,x] = featureVectors(data,sf)
% This function is only in support of Wavelet Toolbox examples.
% It may change or be removed in a future release.
data = single(data);
N = length(data);
dt = 1/1280;
if N < 461
    Ndiff = 461-N;
    pad = Ndiff/2;
    dataUL = [flip(data(1:pad)); data ; ...
                flip(data(N-pad+1:N))];   
     rate = 5e4/3600;
     dx = rate*dt;
     x = 0:dx:(N*dx)-dx;     
elseif N > 461
    Ndiff = N-461;
    zrs = Ndiff/2;
    dataUL = data(zrs:end-zrs-1);
    rate = 3e4/3600;
    dx = rate*dt;
    x = 0:dx:(N*dx)-dx;
else
    dataUL = data;
    rate = 4e4/3600;
    dx = rate*dt;
    x = 0:dx:(N*dx)-dx;
end
fmat = sf.featureMatrix(dataUL);
end

%------------------------------------------------------------------------------
function [mra,chngpts] = helperMRA(data,x)
% This function is only in support of Wavelet Toolbox examples.
% It may change or be removed in a future release.
mra = modwtmra(modwt(data,'sym3'),'sym3');
mraLev = mra(4:6,:);
Ns = size(mraLev,1);
thresh = [2, 4, 8];
chngpts = false(size(mraLev));
% Determine changepoints. We want different thresholds for different
% resolution levels.
for ii = 1:Ns
    chngpts(ii,:) = ischange(mraLev(ii,:),"linear",2,"Threshold",thresh(ii));
end

for kk = 1:Ns
    idx = double(chngpts(kk,:));
    idx(idx == 0) = NaN;    
    subplot(Ns,1,kk)
    plot(x,mraLev(kk,:))
    if kk == 1
        title('MRA Components')
    end
    yyaxis right
    hs = stem(x,idx);
    hs.ShowBaseLine = 'off';
    hs.Marker = '^';
    hs.MarkerFaceColor = [1 0 0];
end
grid on
axis tight
xlabel('Distance (m)')
end