wcoherence

ウェーブレット コヒーレンスとウェーブレット クロス スペクトル

構文

wcoh = wcoherence(x,y)

[wcoh,wcs] = wcoherence(x,y)

[wcoh,wcs,period] = wcoherence(x,y,ts)

[wcoh,wcs,f] = wcoherence(x,y,fs)

[wcoh,wcs,f,coi] = wcoherence(___)

[wcoh,wcs,period,coi] = wcoherence(___,ts)

[___,coi,wtx,wty] = wcoherence(___)

[___] = wcoherence(___,Name=Value)

wcoherence(___)

説明

wcoh = wcoherence(x,y) は、信号 x と y の時間-周波数平面における相関の尺度を示す振幅二乗ウェーブレット コヒーレンスを返します。ウェーブレット コヒーレンスは非定常信号の解析に役立ちます。入力 x と y は、同じ長さの 1 次元の実数値の信号でなければなりません。コヒーレンスは解析 Morlet ウェーブレットを使用して計算されます。

[wcoh,wcs] = wcoherence(x,y) は、x と y の平滑化ウェーブレット クロス スペクトルを返します。クロス スペクトルの値の位相を使用して、入力信号間の相対的な遅れを特定できます。

[wcoh,wcs,period] = wcoherence(x,y,ts) は、正の duration ts をサンプリング間隔として使用します。duration ts を使用して、スケールから周期への変換 period が計算されます。duration 配列 period は、ts で指定した形式と同じ形式です。

[wcoh,wcs,f] = wcoherence(x,y,fs) は、正のサンプリング周波数 fs を使用してスケールから周波数への変換 f を計算します。サンプリング周波数 fs の単位は Hz です。

[wcoh,wcs,f,coi] = wcoherence(___) は、ウェーブレット コヒーレンスの円錐状影響圏 coi をサンプルあたりのサイクル数で返します。サンプリング周波数 fs を指定した場合、円錐状影響圏の単位は Hz です。

[wcoh,wcs,period,coi] = wcoherence(___,ts) は、円錐状影響圏 coi を単位時間あたりのサイクル数で返します。

[___,coi,wtx,wty] = wcoherence(___) は、x および y の連続ウェーブレット変換 (CWT) をそれぞれ wtx、wty に返します。wtx と wty は、ウェーブレット クロス スペクトルおよびウェーブレット コヒーレンスの推定の形成に使用されます。

[___] = wcoherence(___,Name=Value) では、前の構文の入力引数に加えて、1 つ以上の名前と値の引数を使用してオプションを指定します。

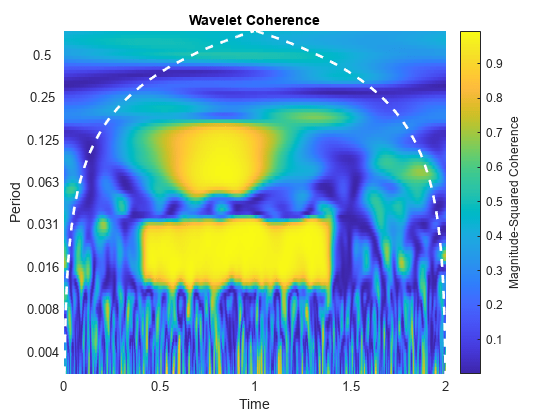
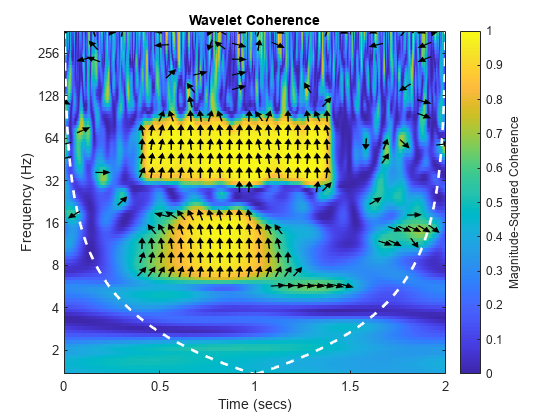
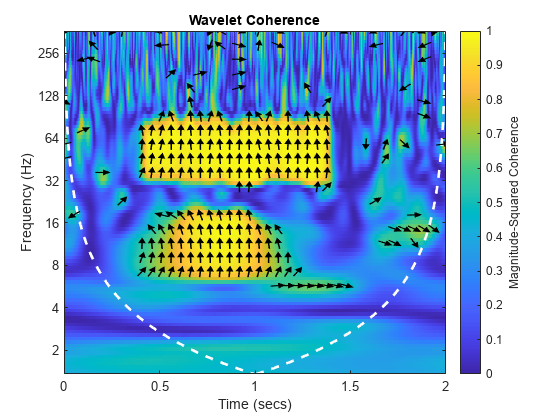
出力引数なしで wcoherence(___) を使用すると、ウェーブレット コヒーレンスと円錐状影響圏が現在の Figure にプロットされます。周波数と周期の逆関数の関係により、サンプリング間隔を使用したプロットはサンプリング周波数を使用したプロットの逆になります。サンプリング周波数を使用したプロットには、コヒーレンスが 0.5 を超える領域について、x に対する y の位相遅れを示す矢印が表示されます。矢印の間隔は時間とスケールに対応します。矢印の方向は単位円上の位相遅れに対応します。たとえば、垂直な矢印は π/2 または 1/4 サイクルの位相遅れを示します。対応する時間の遅れはサイクルの期間によって異なります。

例

2 つの正弦波のウェーブレット コヒーレンス

wcoherence の既定の設定を使用して、ランダムなノイズを含む正弦波と周波数が時間と共に減少する周波数変調信号の間のウェーブレット コヒーレンスを求めます。

t  = linspace(0,1,1024);
x = -sin(8*pi*t) + 0.4*randn(1,1024);
x = x/max(abs(x));
y = wnoise("doppler",10);
wcoh = wcoherence(x,y);

既定のコヒーレンスの計算では、解析 Morlet ウェーブレットが使用されます。オクターブあたりの音の数は 12 で、12 のスケールが平滑化されます。既定のオクターブの数は floor(log2(numel(x)))-1 と等しくなり、この例では 9 です。

ウェーブレット コヒーレンスに対するサンプリング間隔の影響

サンプリング間隔を 0.001 秒に指定して、2 つの信号のウェーブレット コヒーレンスのデータを求めます。どちらの信号もホワイト ノイズに含まれる 2 つの正弦波 (10 Hz と 50 Hz) で構成されます。正弦波の時間のサポートはそれぞれで異なります。

再現性を得るために、乱数発生器を既定の状態に設定します。その後、これらの 2 つの信号を作成します。

rng default
t = 0:0.001:2;
x = cos(2*pi*10*t).*(t>=0.5 & t<1.1)+ ...
    cos(2*pi*50*t).*(t>= 0.2 & t< 1.4)+ ...
    0.25*randn(size(t));
y = sin(2*pi*10*t).*(t>=0.6 & t<1.2)+ ...
    sin(2*pi*50*t).*(t>= 0.4 & t<1.6)+ ...
    0.35*randn(size(t));
tiledlayout(2,1)
nexttile
plot(t,x)
title("X")
nexttile
plot(t,y)
title("Y")
xlabel("Time (seconds)")

2 つの信号のコヒーレンスを求めます。スケールから周期への変換と円錐状影響圏も求めます。

[wcoh,~,period,coi] = wcoherence(x,y,seconds(0.001));

pcolor コマンドを使用して、コヒーレンスと円錐状影響圏をプロットします。

figure
period = seconds(period);
coi = seconds(coi);
h = pcolor(t,log2(period),wcoh);
h.EdgeColor = "none";
ax = gca;
ytick=round(pow2(ax.YTick),3);
ax.YTickLabel=ytick;
ax.XLabel.String="Time";
ax.YLabel.String="Period";
ax.Title.String = "Wavelet Coherence";
hcol = colorbar;
hcol.Label.String = "Magnitude-Squared Coherence";
hold on
plot(ax,t,log2(coi),"w--",linewidth=2)
hold off

出力引数なしで wcoherence(x,y,seconds(0.001)) を使用します。このプロットには、位相の矢印と円錐状影響圏が表示されます。

wcoherence(x,y,seconds(0.001))

ウェーブレット コヒーレンスに対するサンプリング周波数の影響

サンプリング周波数を 1000 Hz に指定して、2 つの信号のウェーブレット コヒーレンスを求めます。どちらの信号もホワイト ノイズに含まれる 2 つの正弦波 (10 Hz と 50 Hz) で構成されます。正弦波の時間のサポートはそれぞれで異なります。

再現性を得るために、乱数発生器を既定の状態に設定し、2 つの信号を作成します。

rng default
t = 0:0.001:2;
x = cos(2*pi*10*t).*(t>=0.5 & t<1.1)+ ...
    cos(2*pi*50*t).*(t>= 0.2 & t< 1.4)+ ...
    0.25*randn(size(t));
y = sin(2*pi*10*t).*(t>=0.6 & t<1.2)+ ...
    sin(2*pi*50*t).*(t>= 0.4 & t<1.6)+ ...
    0.35*randn(size(t));

ウェーブレット コヒーレンスを求めます。コヒーレンスのプロットは、サンプリング周波数ではなくサンプリング間隔を指定した前の例のプロットを反転したものになります。

wcoherence(x,y,1000)

ウェーブレット コヒーレンスに対する平滑化スケールの数の影響

1000 Hz でサンプリングされた 2 つの信号のウェーブレット コヒーレンスを求めます。どちらの信号もホワイト ノイズに含まれる 2 つの正弦波 (10 Hz と 50 Hz) で構成されます。平滑化するスケールの数の既定値を使用します。この値はオクターブあたりの音の数と等価です。どちらの値も既定で 12 になります。

再現性を得るために、乱数発生器を既定の状態に設定します。その後、2 つの信号を作成し、コヒーレンスを求めます。

rng default
Fs = 1000;
t = 0:1/Fs:2;
x = cos(2*pi*10*t).*(t>=0.5 & t<1.1)+ ...
    cos(2*pi*50*t).*(t>= 0.2 & t< 1.4)+ ...
    0.25*randn(size(t));
y = sin(2*pi*10*t).*(t>=0.6 & t<1.2)+ ...
    sin(2*pi*50*t).*(t>= 0.4 & t<1.6)+ ...
    0.35*randn(size(t));
wcoherence(x,y,Fs)

平滑化するスケールの数を 18 に設定します。平滑化が増えるため、低周波数の分解能が減少します。

wcoherence(x,y,Fs,NumScalesToSmooth=18)

気象データのウェーブレット コヒーレンスに対する位相表示しきい値の影響

異なる位相表示しきい値を使用してウェーブレット コヒーレンスに対する影響を比較します。

エルニーニョの時系列とインド全域の平均雨量指数の間のウェーブレット コヒーレンスをプロットします。データは月ごとにサンプリングされています。サンプリング間隔を 1 年の 1/12 と指定して年単位で周期を表示します。既定の位相表示しきい値 0.5 を使用し、コヒーレンスが 0.5 以上の場合にのみ位相の矢印が表示されるようにします。

load ninoairdata
wcoherence(nino,air,years(1/12))

位相表示しきい値を 0.7 に設定します。位相矢印の数が減っていることを確認します。

wcoherence(nino,air,years(1/12),PhaseDisplayThreshold=0.7);

入力引数

x — 入力信号

実数値のベクトル

入力信号。実数値のベクトルとして指定します。x は 1 次元の実数値の信号でなければなりません。2 つの入力信号 x と y は同じ長さでなければならず、少なくとも 4 つのサンプルを含まなければなりません。

y — 入力信号

実数値のベクトル

入力信号。実数値のベクトルとして指定します。y は 1 次元の実数値の信号でなければなりません。2 つの入力信号 x と y は同じ長さでなければならず、少なくとも 4 つのサンプルを含まなければなりません。

ts — サンプリング間隔

正のスカラー入力をもつ duration

サンプリング間隔 (サンプリング周期とも呼ばれます)。正のスカラー入力をもつ duration として指定します。有効な duration は、years、days、hours、seconds、および minutes です。関数 duration を使用して ts を指定することもできます。カレンダー期間 (caldays、calweeks、calmonths、calquarters、calyears) は使用できません。

サンプリング周波数 fs とサンプリング周期 ts の両方を指定することはできません。

fs — サンプリング周波数

正のスカラー | []

サンプリング周波数。正のスカラーとして指定します。

fs を空として指定した場合、wcoherence は、サイクル/サンプルの単位で正規化周波数を使用します。ナイキスト周波数は ½ です。

サンプリング周波数 fs とサンプリング周期 ts の両方を指定することはできません。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

例: wcoh = wcoherence(x,y,PhaseDisplayThreshold=0.7) は、位相ベクトルを表示するしきい値を指定します。

R2021a より前では、コンマを使用して名前と値をそれぞれ区切り、Name を引用符で囲みます。

例: wcoh = wcoherence(x,y,"PhaseDisplayThreshold",0.7) は、位相ベクトルを表示するしきい値を指定します。

FrequencyLimits — 周波数の範囲

2 要素スカラー ベクトル

wcoherence で使用する周波数の範囲。厳密に増加する正の要素をもつ 2 要素ベクトルとして指定します。

• 最初の要素は最も低いピーク通過帯域周波数を示し、ウェーブレットのピーク周波数 (Hz 単位) と 2 つの時間の標準偏差の積を信号長で除算した値以上でなければなりません。

• 2 番目の要素は最も高いピーク通過帯域周波数を示し、ナイキスト周波数以下でなければなりません。

最小周波数に対する最大周波数の比の基底 2 の対数は 1/NV 以上でなければなりません。ここで NV はオクターブあたりの音の数です。

許容される範囲外の周波数範囲を指定した場合、wcoherence では有効な最小値と最大値まで範囲が切り詰められます。ウェーブレット コヒーレンスの各種パラメーター表現に対する周波数範囲を特定するには、ウェーブレットを "amor" に設定して cwtfreqbounds を使用します。

例: FrequencyLimits=[0.1 0.3]

PeriodLimits — 周期の範囲

2 要素 duration 配列

wcoherence で使用する周期の範囲。厳密に増加する正の要素をもつ 2 要素 duration 配列として指定します。最初の要素は 2×ts 以上でなければなりません。ここで ts はサンプリング周期です。最大周期に対する最小周期の比の基底 2 の対数は -1/NV 以下でなければなりません。ここで NV はオクターブあたりの音の数です。最大周期は、ウェーブレットの 2 つの時間の標準偏差とウェーブレットのピーク周波数の積で信号長を除算した値を超えることはできません。

許容される範囲外の周期範囲を指定した場合、wcoherence では有効な最小値と最大値まで範囲が切り詰められます。ウェーブレット コヒーレンスの各種パラメーター表現に対する周期範囲を特定するには、ウェーブレットを "amor" に設定して cwtfreqbounds を使用します。

例: PeriodLimits=[seconds(0.2) seconds(1)]

データ型: duration

VoicesPerOctave — オクターブあたりの音の数

12 (既定値) | 10 から 32 までの偶数の整数

ウェーブレット コヒーレンスで使用するオクターブあたりの音の数。10 から 32 までの偶数の整数として指定します。

NumScalesToSmooth — 平滑化するスケールの数

正の整数

時間とスケールで平滑化するスケールの数。N の 1/2 以下の正の整数として指定します。ここで、N はウェーブレット変換のスケールの数です。NumScalesToSmooth を指定しない場合、既定で floor(N/2) と VoicesPerOctave の最小値になります。この関数では、移動平均フィルターを使用してスケール全体が平滑化されます。コヒーレンスにノイズが含まれる場合は、指定する NumScalesToSmooth の値を大きくすることでコヒーレンスをさらに平滑化できます。

NumOctaves — オクターブの数

floor(log2(numel(x)))-1 (既定値) | 正の整数

ウェーブレット コヒーレンスで使用するオクターブの数。1 から floor(log2(numel(x)))-1 までの正の整数として指定します。低い周波数の値を調べる必要がない場合は、NumOctaves の値を小さくします。

名前と値の引数 NumOctaves は非推奨であり、将来のリリースで削除される予定です。ウェーブレット コヒーレンスの周波数または周期の範囲を変更するときは、名前と値の引数 'FrequencyLimits' または 'PeriodLimits' を使用することを推奨します。'NumOctaves' と 'FrequencyLimits' または 'PeriodLimits' の両方の名前と値の引数を指定することはできません。cwtfreqbounds を参照してください。

PhaseDisplayThreshold — 位相ベクトルを表示するしきい値

0.5 (既定値) | 0 ～ 1 の実数のスカラー

位相ベクトルを表示するしきい値。0 ～ 1 の実数のスカラーとして指定します。この関数では、コヒーレンスが指定したしきい値以上の領域について位相ベクトルが表示されます。しきい値を小さいほど、多くの位相ベクトルが表示されます。出力引数なしで wcoherence を使用した場合は PhaseDisplayThreshold の値は無視されます。

出力引数

wcoh — ウェーブレット コヒーレンス

行列

ウェーブレット コヒーレンス。行列として返されます。コヒーレンスは解析 Morlet ウェーブレットを使用して対数スケールで計算されます。オクターブあたりの音の数の既定値は 12 です。既定のオクターブの数は floor(log2(numel(x)))-1 と等しくなります。サンプリング間隔を指定しない場合、サンプリング周波数と仮定されます。

詳細については、ウェーブレット コヒーレンスを参照してください。

wcs — 平滑化ウェーブレット クロス スペクトル

複素数値の行列

平滑化ウェーブレット クロス スペクトル。複素数値の行列として返されます。クロス スペクトルの値の位相を使用して、入力信号間の相対的な遅れを特定できます。

詳細については、平滑化ウェーブレット クロス スペクトルを参照してください。

period — スケールから周期への変換

duration の配列

スケールから周期への変換。duration の配列として返されます。変換値は ts で指定したサンプリング周期から計算されます。period の各要素の形式は ts と同じになります。

f — スケールから周波数への変換

ベクトル

スケールから周波数への変換。ベクトルとして返されます。このベクトルには、コヒーレンスの計算に使用されるウェーブレットのピーク周波数の値が含まれます。f を出力する場合にサンプリング周波数入力 fs を指定していないと、返されるウェーブレット コヒーレンスはサンプルあたりのサイクル数になります。

coi — 円錐状影響圏

double の配列 | duration の配列

ウェーブレット コヒーレンスの円錐状影響圏。double の配列または duration の配列のいずれかとして返されます。円錐状影響圏は、コヒーレンスのデータでエッジの影響が現れる箇所を示します。サンプリング周波数 fs を指定した場合、円錐状影響圏の単位は Hz です。サンプリング間隔 (周期) ts を指定した場合、円錐状影響圏の単位は周期です。エッジの影響により、円錐状影響圏の外側やそれと重なるコヒーレンスの高い領域は信頼性が低くなります。円錐状影響圏は破線で示されます。

詳細については、Boundary Effects and the Cone of Influenceを参照してください。

wtx — x の連続ウェーブレット変換

行列

x の連続ウェーブレット変換。行列として返されます。

wty — y の連続ウェーブレット変換

行列

y の連続ウェーブレット変換。行列として返されます。

詳細

平滑化ウェーブレット クロス スペクトル

平滑化ウェーブレット クロス スペクトルは、2 つの信号のパワーの分布の尺度です。

2 つの時系列 x と y の平滑化ウェーブレット クロス スペクトルは次のとおりです。

$$C_{xy}(a,b)=S(C_x(a,b)C_y^{*}(a,b)),$$

ここで、C_x(a,b) と C_y(a,b) は、スケール a および位置 b における x と y の連続ウェーブレット変換を示します。上付き文字 * は複素共役で、S は時間とスケールの平滑化演算子です。

実数値の時系列についてのウェーブレット クロス スペクトルは、実数値の解析ウェーブレットを使用した場合は実数値、複素数値の解析ウェーブレットを使用した場合は複素数値になります。

ウェーブレット コヒーレンス

ウェーブレット コヒーレンスは、2 つの信号間の相関の尺度です。

2 つの時系列 x と y のウェーブレット コヒーレンスは次のとおりです。

$$\frac{{\left|S(C_x(a,b)C_y^{*}(a,b))\right|}^2}{S(|C_x(a,b){|}^2)·S(|C_y(a,b){|}^2)},$$

ここで、C_x(a,b) と C_y(a,b) は、スケール a および位置 b における x と y の連続ウェーブレット変換を示します。上付き文字 * は複素共役で、S は時間とスケールの平滑化演算子です。

実数値の時系列についてのウェーブレット コヒーレンスは、実数値の解析ウェーブレットを使用した場合は実数値、複素数値の解析ウェーブレットを使用した場合は複素数値になります。

ヒント

• 平滑化されていないウェーブレット クロス スペクトルを取得するには、次のようにしてオプションの出力 wtx と wty を使用します。

  unsmoothedWCS = wtx.*conj(wty);

参照

[1] Grinsted, A., J. C. Moore, and S. Jevrejeva. “Application of the Cross Wavelet Transform and Wavelet Coherence to Geophysical Time Series.” Nonlinear Processes in Geophysics 11, no. 5/6 (November 18, 2004): 561–66. https://doi.org/10.5194/npg-11-561-2004.

[2] Maraun, D., J. Kurths, and M. Holschneider. “Nonstationary Gaussian Processes in Wavelet Domain: Synthesis, Estimation, and Significance Testing.” Physical Review E 75, no. 1 (January 22, 2007): 016707. https://doi.org/10.1103/PhysRevE.75.016707.

[3] Torrence, Christopher, and Peter J. Webster. “Interdecadal Changes in the ENSO–Monsoon System.” Journal of Climate 12, no. 8 (August 1999): 2679–90. https://doi.org/10.1175/1520-0442(1999)012<2679:ICITEM>2.0.CO;2.

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

• 次の入力引数はサポートされていません。ts (サンプリング周期)、PeriodLimits 名前と値の引数、および PhaseDisplayThreshold 名前と値の引数。

• duration データ型はサポートされていません。

• プロットはサポートされていません。

GPU コード生成

GPU Coder™ を使用して NVIDIA® GPU のための CUDA® コードを生成します。

使用上の注意および制限:

• 次の入力引数はサポートされていません。ts (サンプリング周期)、PeriodLimits 名前と値の引数、および PhaseDisplayThreshold 名前と値の引数。

• duration データ型はサポートされていません。

• プロットはサポートされていません。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

この関数は、GPU 配列を完全にサポートします。詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2016a で導入

R2023b: GPU コードの生成

関数 wcoherence は CUDA^® コード生成をサポートします。CUDA コードを生成するには、MATLAB^® Coder™ および GPU Coder™ が必要です。

R2020a: 'NumOctaves' の名前と値の引数は削除予定

'NumOctaves' の名前と値の引数は、将来のリリースで削除される予定です。次のいずれかを使用してください。

• ウェーブレット コヒーレンスの周波数範囲を変更する場合は名前と値の引数 'FrequencyLimits'。

• ウェーブレット コヒーレンスの周期範囲を変更する場合は名前と値の引数 'PeriodLimits'。

詳細については、cwtfreqbounds を参照してください。

参考

オブジェクト

• cwtfilterbank

関数

• cwt | cwtfreqbounds

トピック

• Practical Introduction to Time-Frequency Analysis Using the Continuous Wavelet Transform
• Relative Velocity Changes in Seismic Waves Using Time-Frequency Analysis