ウェーブレット コヒーレンスを使用した信号の時間-周波数成分の比較
この例では、ウェーブレット コヒーレンスとウェーブレット クロススペクトルを使用して、2 つの時系列における時間局在型の共通の振動動作を識別する方法を示します。また、この例では、ウェーブレット コヒーレンスとウェーブレット クロススペクトルを、対応するフーリエ コヒーレンスとフーリエ クロススペクトルと比較します。mscohere (Signal Processing Toolbox)とcpsd (Signal Processing Toolbox)を使用してこれらの例を実行するには、Signal Processing Toolbox™ が必要です。
多くのアプリケーションでは、2 つの時系列に共通するパターンの識別と特徴付けを行います。ある状況では、2 つの時系列の共通の動作は、1 つの時系列がもう 1 つの時系列を駆動する、または影響を与えることで生じる場合があります。別の状況では、共通するパターンは、両方の時系列に影響するいくつかの観測されないメカニズムから生じる場合もあります。
共に定常的な時系列の場合、時間または周波数において相関する動作を特徴付ける標準的な手法は、相互相関、(フーリエ) クロス スペクトル、コヒーレンスです。ただし、多くの時系列は非定常です。つまり、その周波数成分は時間の経過と共に変化します。これらの時系列では、時間-周波数平面における相関またはコヒーレンスの尺度をもつことが重要です。
ウェーブレット コヒーレンスを使用すれば、非定常信号で共通の時間局在型の振動を検出できます。1 つの時系列が別の時系列に影響を与えていることが自然に見られる状況では、ウェーブレット クロススペクトルの位相を使用して 2 つの時系列間の相対ラグを識別できます。
共通する時間局在型の振動の特定と位相遅れの判別
最初の例では、10 Hz と 75 Hz の時間局在型の振動から構成される 2 つの信号を使用します。信号の持続時間は 6 秒で 1000 Hz でサンプリングしています。2 つの信号の 10 Hz の振動は 1.2 ~ 3 秒の間でオーバーラップします。75 Hz の振動のオーバーラップは 0.4 ~ 4.4 秒の間で発生します。10 Hz 成分と 75 Hz 成分は、Y 信号の 1/4 サイクル遅延します。これは、2 つの信号の 10 Hz 成分と 75 Hz 成分の間に (90 度) の位相遅れがあることを意味します。両方の信号が加法性ホワイト ガウス ノイズによって破損します。
load wcoherdemosig1 subplot(2,1,1) plot(t,x1) title('X Signal') grid on ylabel('Amplitude') subplot(2,1,2) plot(t,y1) title('Y Signal') ylabel('Amplitude') grid on xlabel('Seconds')

ウェーブレット コヒーレンスを取得し、結果を表示します。サンプリング周波数 (1000 Hz) を入力し、ウェーブレット コヒーレンスの時間周波数プロットを求めます。コヒーレンスが 0.5 を超える時間-周波数平面の領域内で、ウェーブレット クロススペクトルからの位相を使用してコヒーレントな成分間の相対的な遅れを示します。位相は特定方向を指す矢印によって示されます。特定の周波数の Y 信号の 1/4 サイクルの遅れは、垂直方向を指す矢印によって示されていることに注意してください。
figure wcoherence(x1,y1,1000)

10 Hz と 75 Hz のコヒーレントな振動動作の 2 つの時間局在型の領域は、ウェーブレット コヒーレンスのプロットでは明確です。位相の関係は、コヒーレンスの高い領域の矢印の向きによって示されます。この例では、ウェーブレット クロススペクトルが、10 Hz と 75 Hz の 2 つの信号間で (1/4 サイクル) の位相遅れを捉えていることがわかります。
白い破線は、エッジの影響が異なる周波数 (スケール) で顕著になる円錐状影響圏を示します。円錐状影響圏外または重複する円錐状影響圏内のコヒーレンスの高い領域を解釈する場合には注意が必要です。
フーリエ振幅二乗コヒーレンスおよびクロススペクトルを使用して同じ解析を繰り返します。
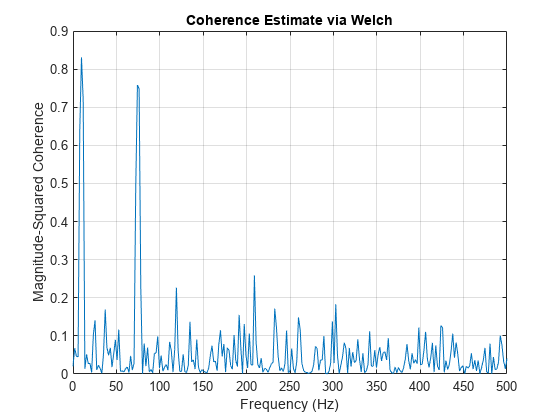
figure mscohere(x1,y1,500,450,[],1000)
[Pxy,F] = cpsd(x1,y1,500,450,[],1000); Phase = (180/pi)*angle(Pxy); figure plot(F,Phase) title('Cross-Spectrum Phase') xlabel('Hz') ylabel('Phase (Degrees)') grid on ylim([0 180]) xlim([0 200]) hold on plot([10 10],[0 180],'r--') plot([75 75],[0 180],'r--') plot(F,90*ones(size(F)),'r--') hold off

mscohere (Signal Processing Toolbox)から取得したフーリエ振幅二乗コヒーレンスは、10 Hz と 75 Hz のコヒーレントな振動を明確に判別します。フーリエ クロススペクトルの位相のプロットで、赤い縦の破線は 10 Hz と 75 Hz をマークし、横の破線は 90 度の角度をマークします。クロススペクトルの位相が、成分間の相対的な位相遅れを捉える妥当な処理を行っていることがわかります。
しかし、コヒーレントな動作の時間に依存する性質は、これらの手法では完全に不明瞭です。非定常信号の場合、時間-周波数平面におけるコヒーレントな動作の特徴付けの方がさらに多くの情報を提供します。
次の例では、2 つの信号間の位相関係が変化する間に前述のものを繰り返します。この場合、Y 信号の 10 Hz 成分は 3/8 サイクル ( ラジアン) 遅延します。Y 信号の 75 Hz 成分は 1/8 サイクル ( ラジアン) 遅延します。ウェーブレット コヒーレンスおよび位相によってコヒーレンスが 0.75 を超える領域のみが表示されるしきい値をプロットします。
load wcoherdemosig2 wcoherence(x2,y2,1000,'phasedisplaythreshold',0.75)

ウェーブレット クロススペクトルから得られる位相推定は、10 Hz と 75 Hz の 2 つの時系列間の相対的な遅れを捉えます。
周波数ではなく周期単位でデータを表示する場合、MATLAB duration オブジェクトを使用してサンプル時間を wcoherence に与えることができます。
wcoherence(x2,y2,seconds(0.001),'phasedisplaythreshold',0.75)
ウェーブレット コヒーレンスが周期単位でプロットされるようになったため、円錐状影響圏が反転することに注意してください。
気候データにおけるコヒーレントな振動および遅延の判別
El Nino Region 3 データと、1871 年から 2003 年後半の季節に無関係なすべてのインドの雨量指数を読み込んでプロットします。データは月ごとにサンプリングされています。Nino 3 の時系列は、西経 90 度から西経 150 度および北緯 5 度から南緯 5 度で、赤道太平洋から記録された月次の海面温度の異常を摂氏で表した記録です。すべてのインドの雨量指数は、季節成分を削除した平均的なインドの雨量をミリメートルで表します。
load ninoairdata figure subplot(2,1,1) plot(datayear,nino) title('El Nino Region 3 -- SST Anomalies') ylabel('Degrees Celsius') axis tight subplot(2,1,2) plot(datayear,air) axis tight title('Deseasonalized All Indian Rainfall Index') ylabel('Millimeters') xlabel('Year')

位相推定値を使用してウェーブレット コヒーレンスをプロットします。このデータの場合、振動を年の周期単位で見る方がより自然です。出力周期が年単位となるように年を単位とする duration オブジェクトとして、サンプリング間隔 (周期) を入力します。振幅二乗コヒーレンスが 0.7 を超える 2 つの気候の時系列間のみの相対的な遅れを示します。
figure
wcoherence(nino,air,years(1/12),'phasedisplaythreshold',0.7)
プロットは、通常のエルニーニョのサイクルである 2 年から 7 年に該当する周期に発生する強力なコヒーレンスの時間局在型の領域を示します。プロットは、これらのサイクルの 2 つの時系列間で約 3/8 から 1/2 サイクルの遅延があることも示します。これは、南アメリカ沿岸沖で記録されたエルニーニョと一致する海の温暖化のサイクルが、約 17,000 km 離れたインドの雨量と相関性があるが、この影響は約 1/2 サイクル (1 年から 3.5 年) 遅延することを示します。
脳の活動におけるコヒーレントな振動の検出
以前の例では、1 つの時系列が他方に影響を与えるものとして表示することが自然でした。このような場合、データ間のリードラグ関係を調べることが有用です。場合によっては、コヒーレンスを単独で調べる方がより自然です。
たとえば、2 人の被験者から取得した近赤外線分光法 (NIRS) データを検討します。NIRS は、酸素化ヘモグロビンおよび脱酸素化ヘモグロビンの異なる吸収の特性を利用して、脳の活動を測定します。データは Cui, Bryant & Reiss[1]によるもので、この例のために著者に提供していただきました。記録部位は両被験者の上前頭皮質でした。データは 10 Hz でサンプリングされます。実験では、被験者はタスクに対して協力と競争を繰り返しました。タスクの周期は約 7.5 秒でした。
load NIRSData figure plot(tm,NIRSData(:,1)) hold on plot(tm,NIRSData(:,2),'r') legend('Subject 1','Subject 2','Location','NorthWest') xlabel('Seconds') title('NIRS Data') grid on hold off

ウェーブレット コヒーレンスを時間および周波数の関数として取得します。wcoherence を使用して、ウェーブレット コヒーレンス、クロススペクトル、スケールから周波数またはスケールから周期の変換および円錐状影響圏を出力できます。この例では、補助関数 helperPlotCoherence が wcoherence の出力をプロットするための便利なコマンドをいくつかパッケージ化しています。
[wcoh,~,F,coi] = wcoherence(NIRSData(:,1),NIRSData(:,2),10,'numscales',16); helperPlotCoherence(wcoh,tm,F,coi,'Seconds','Hz')

プロットでは、1 Hz 付近のデータ収集周期全体の強力なコヒーレンスの領域がわかります。これは 2 人の被験者の心調律に起因します。さらに、0.13 Hz 付近の強力なコヒーレンスの領域がわかります。これはタスクに起因する被験者の脳内のコヒーレントな振動を表します。ウェーブレット コヒーレンスを周波数ではなく周期の単位で表示することがより自然である場合、サンプリング間隔を duration オブジェクトとして入力できます。wcoherence はスケールから周期の変換を提供します。
[wcoh,~,P,coi] = wcoherence(NIRSData(:,1),NIRSData(:,2),seconds(0.1),... 'numscales',16); helperPlotCoherence(wcoh,tm,seconds(P),seconds(coi),... 'Time (secs)','Periods (Seconds)')

ここでも、約 1 秒の周期で記録全体で発生している被験者の心臓の活動に対応するコヒーレントな振動に注意してください。タスクに関係する活動は、約 8 秒の周期にも表れます。このデータのウェーブレット解析の詳細については、Cui, Bryant, & Reiss[1]を参照してください。
まとめ
この例では、ウェーブレット コヒーレンスを使用して、2 つの時系列における時間局在型の振動動作を調査する方法について説明しました。非定常信号の場合、同時時間および周波数 (周期) 情報を提供するコヒーレンスの測定方法があると、さらに多くの情報が得られることがよくあります。1 つの時系列が他方の振動に直接影響を与える場合に、ウェーブレット クロススペクトルから取得した相対的な位相情報の情報量が多くなる可能性があります。
付録
この例では次の補助関数が使用されています。
参照
[1] Cui, X., D. M. Bryant, and A. L. Reiss. "NIRS-Based Hyperscanning Reveals Increased Interpersonal Coherence in Superior Frontal Cortex during Cooperation." Neuroimage. Vol. 59, Number 3, 2012, pp. 2430–2437.
[2] Grinsted, A., J. C. Moore, and S. Jevrejeva. "Application of the cross wavelet transform and wavelet coherence to geophysical time series." Nonlinear Processes in Geophysics. Vol. 11, 2004, pp. 561–566. doi:10.5194/npg-11-561-2004.
[3] Maraun, D., J. Kurths, and M. Holschneider. "Nonstationary Gaussian processes in wavelet domain: synthesis, estimation, and significance testing." Physical Review E. Vol. 75, 2007, pp. 016707(1)–016707(14). doi:10.1103/PhysRevE.75.016707.
[4] Torrence, C., and P. Webster. "Interdecadal Changes in the ENSO-Monsoon System." Journal of Climate. Vol. 12, Number 8, 1999, pp. 2679–2690. doi:10.1175/1520-0442(1999)012<2679:ICITEM>2.0.CO;2.