このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
さまざまな路面でのヨー安定性
この例では、さまざまな路面で車両運動のダブルレーン チェンジ操縦を実行して車両のヨー安定性を解析し、操縦が成功するかどうかを確認する方法を示します。
車両の障害物回避性能をテストするためのダブルレーン チェンジ操縦が ISO 3888-2 で定義されています。このテストでのドライバーの操作は次のとおりです。
車両がターゲット速度に達するまで加速する
アクセル ペダルを放す
ステアリング ホイールを回して左車線に入る
ステアリング ホイールを回して右車線に戻る
一般に、車線境界線はコーンで示されます。車両とドライバーがコーンに当たらずに通過できれば、車両はテストにパスします。
リファレンス アプリケーションの詳細については、ダブルレーン チェンジ操縦を参照してください。
helpersetupdlc;

ダブルレーン チェンジ操縦の実行
1. Lane Change Reference Generator ブロックを開きます。既定では、操縦のパラメーターは次のように設定されています。
縦方向進入速度の設定点 — 35 mph
車両幅 — 2 m
横方向の基準位置ブレークポイント、横方向の参照データ — 横方向の基準軌跡を縦方向の距離の関数として指定する値
2. Visualization サブシステムで 3D Engine ブロックを開きます。既定では、[3D エンジン] パラメーターは [無効] に設定されています。3D 可視化環境でモデルのシミュレーションを実行するには、Simulink® 3D Animation™ が必要です。3D 可視化エンジンのプラットフォームの要件やハードウェアの推奨事項については、Unreal Engine シミュレーション環境の要件と制限を参照してください。
3. 操縦を実行します。シミュレーションを実行しながら、車両の情報を確認します。
mdl = 'DLCReferenceApplication';
sim(mdl);
### Searching for referenced models in model 'DLCReferenceApplication'. ### Total of 3 models to build. ### Starting serial model build. ### Successfully updated the model reference simulation target for: Driveline ### Successfully updated the model reference simulation target for: PassVeh14DOF ### Successfully updated the model reference simulation target for: SiMappedEngineV Build Summary Model reference simulation targets: Model Build Reason Status Build Duration ================================================================================================================= Driveline Target (Driveline_msf.mexw64) did not exist. Code generated and compiled. 0h 0m 27.52s PassVeh14DOF Target (PassVeh14DOF_msf.mexw64) did not exist. Code generated and compiled. 0h 1m 46.001s SiMappedEngineV Target (SiMappedEngineV_msf.mexw64) did not exist. Code generated and compiled. 0h 0m 16.022s 3 of 3 models built (0 models already up to date) Build duration: 0h 2m 35.446s

[Vehicle Position] ウィンドウで、車両の縦方向の距離を横方向の距離の関数として表示します。
Visualization サブシステムで、Lane Change Scope ブロックを開き、横方向の変位を時間の関数として表示します。赤とオレンジの線はコーンによる境界線を示します。青の線は基準軌跡、緑の線は実際の軌跡を示します。緑の線は、コーンを示す赤の線に近づきません。

Visualization サブシステムで、3D Engine ブロックの可視化環境を有効にすると、車両の応答を
AutoVrtlEnvウィンドウで確認できます。

表面摩擦のスイープ
摩擦のスケーリング係数がそれぞれ異なる 3 つの路面でリファレンス アプリケーションを実行します。結果を使用してヨー安定性を解析します。これは、操縦が成功するかどうかを確認するのに役立ちます。
1. ダブルレーン チェンジ リファレンス アプリケーション モデル DLCReferenceApplication で、Environment サブシステムを開きます。摩擦のスケーリング係数は Friction ブロックのパラメーター [定数値] で指定します。既定では、摩擦のスケーリング係数は 1.0 です。リファレンス アプリケーションでは、この係数を使用して各タイム ステップにおける摩擦を調整します。
2. 速度、車線、および ISO の各信号の信号ログを有効にします。Simulink® エディターを使用するか、あるいは以下の MATLAB® コマンドを使用できます。モデルを保存します。
Lane Change Reference Generator の Lane 出力端子信号の信号ログを有効にします。
mdl = 'DLCReferenceApplication'; ph=get_param('DLCReferenceApplication/Lane Change Reference Generator','PortHandles'); set_param(ph.Outport(1),'DataLogging','on');
Passenger Vehicle ブロックの出力端子信号の信号ログを有効にします。

ph=get_param('DLCReferenceApplication/Passenger Vehicle','PortHandles'); set_param(ph.Outport(1),'DataLogging','on');
Visualization サブシステムで、ISO ブロックの信号ログを有効にします。

set_param([mdl '/Visualization/ISO 15037-1:2006'],'Measurement','Enable');
3. 調査する摩擦のスケーリング係数のベクトル lambdamu を設定します。たとえば、0.9、0.95、および 1.0 に等しい摩擦のスケーリング係数について調べるには、コマンド ラインで次のように入力します。
lambdamu = [0.9, 0.95, 1.0]; numExperiments = length(lambdamu);
4. lambdamu を Friction の定数のブロック パラメーターと等しくなるように設定するシミュレーション入力の配列を作成します。
for idx = numExperiments:-1:1 in(idx) = Simulink.SimulationInput(mdl); in(idx) = in(idx).setBlockParameter([mdl '/Environment/Friction'],... 'Value',['ones(4,1).*',num2str(lambdamu(idx))]); end
5. シミュレーション終了時間を 25 秒に設定します。モデルを保存し、シミュレーションを実行します。利用可能な場合は並列計算を使用します。
set_param(mdl,'StopTime','25') save_system(mdl) tic; simout = parsim(in,'ShowSimulationManager','on'); toc;
[27-Dec-2024 11:21:09] Checking for availability of parallel pool... [27-Dec-2024 11:21:09] Starting Simulink on parallel workers... [27-Dec-2024 11:21:12] Loading project on parallel workers... [27-Dec-2024 11:21:12] Configuring simulation cache folder on parallel workers... [27-Dec-2024 11:21:12] Loading model on parallel workers... [27-Dec-2024 11:21:35] Running simulations... [27-Dec-2024 11:22:32] Completed 1 of 3 simulation runs [27-Dec-2024 11:22:32] Received simulation output (size: 11.97 MB) for run 3 from parallel worker. [27-Dec-2024 11:22:56] Completed 2 of 3 simulation runs [27-Dec-2024 11:22:56] Received simulation output (size: 12.96 MB) for run 2 from parallel worker. [27-Dec-2024 11:23:26] Completed 3 of 3 simulation runs [27-Dec-2024 11:23:26] Received simulation output (size: 14.15 MB) for run 1 from parallel worker. [27-Dec-2024 11:23:26] Cleaning up parallel workers... Elapsed time is 150.337127 seconds.
6. シミュレーションが完了したら、シミュレーション データ インスペクターのウィンドウを閉じます。
シミュレーション データ インスペクターを使用した結果の解析
シミュレーション データ インスペクターを使用して結果を調べます。UI を使用するか、あるいはコマンド ライン関数を使用できます。
1. シミュレーション データ インスペクターを開きます。Simulink ツールストリップで、[シミュレーション] タブの [結果の確認] にある [データ インスペクター] をクリックします。
シミュレーション データ インスペクターで [インポート] を選択します。

[インポート] ダイアログ ボックスで
logsoutをクリアします。simout(1)、simout(2)、およびsimout(3)を選択します。[インポート] を選択します。

シミュレーション データ インスペクターを使用して結果を調べます。
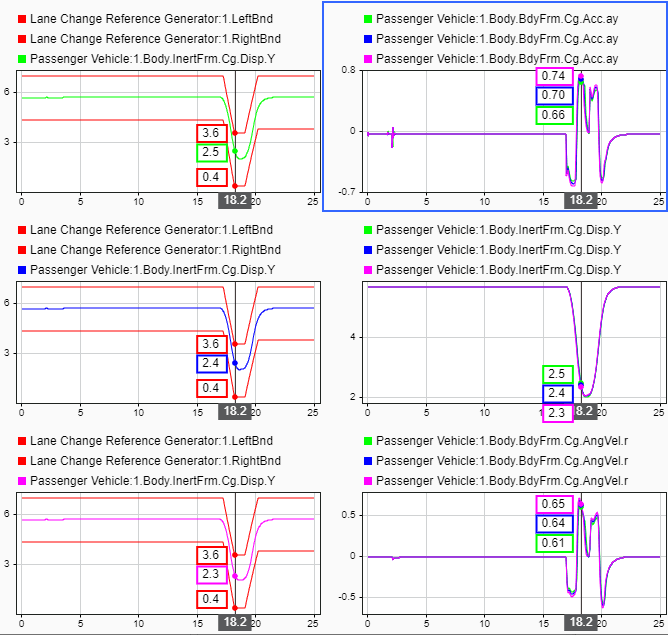
2. あるいは、次の MATLAB コマンドを使用して 6 つのプロットを作成します。最初の 3 つのプロットは、各実行についての車線境界線の上限 UB、車線境界線の下限 LB、および車両の横方向の距離 Y を示します。
次の 3 つのプロットは、各実行についての横方向加速度 ay、車両の横方向の距離 Y、およびヨー レート r を示します。
for idx = 1:numExperiments % Create sdi run object simoutRun(idx)=Simulink.sdi.Run.create; simoutRun(idx).Name=['lambdamu = ', num2str(lambdamu(idx))]; add(simoutRun(idx),'vars',simout(idx)); end sigcolor=[1 0 0]; for idx = 1:numExperiments % Extract the maneuver upper and lower lane boundaries ubsignal(idx)=getSignalsByName(simoutRun(idx), 'Lane Change Reference Generator:1.LeftBnd'); ubsignal(idx).LineColor = sigcolor; lbsignal(idx)=getSignalsByName(simoutRun(idx), 'Lane Change Reference Generator:1.RightBnd'); lbsignal(idx).LineColor = sigcolor; end sigcolor=[0 1 0;0 0 1;1 0 1]; for idx = 1:numExperiments % Extract the lateral acceleration, position, and yaw rate ysignal(idx)=getSignalsByName(simoutRun(idx), 'Passenger Vehicle:1.Body.InertFrm.Cg.Disp.Y'); ysignal(idx).LineColor =sigcolor((idx),:); rsignal(idx)=getSignalsByName(simoutRun(idx), 'Passenger Vehicle:1.Body.BdyFrm.Cg.AngVel.r'); rsignal(idx).LineColor =sigcolor((idx),:); asignal(idx)=getSignalsByName(simoutRun(idx), 'Passenger Vehicle:1.Body.BdyFrm.Cg.Acc.ay'); asignal(idx).LineColor =sigcolor((idx),:); end Simulink.sdi.view Simulink.sdi.setSubPlotLayout(numExperiments,2); for idx = 1:numExperiments % Plot the lateral position and lane boundaries plotOnSubPlot(ubsignal(idx),(idx),1,true); plotOnSubPlot(lbsignal(idx),(idx),1,true); plotOnSubPlot(ysignal(idx),(idx),1,true); end for idx = 1:numExperiments % Plot the lateral acceleration, position, and yaw rate plotOnSubPlot(asignal(idx),1,2,true); plotOnSubPlot(ysignal(idx),2,2,true); plotOnSubPlot(rsignal(idx),3,2,true); end
結果は次のプロットのようになり、摩擦のスケーリング係数が 1 と等しい場合の車両のヨー レートが約 .66 rad/s になることがわかります。
追加の解析
結果をさらに調べるために、次のコマンドを使用して、横方向加速度、ステアリング角度、および車両の軌跡を simout オブジェクトから抽出します。
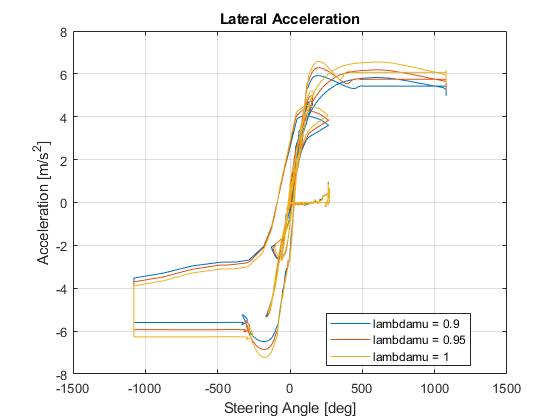
1. 横方向加速度とステアリング角度を抽出します。データをプロットします。結果は次のプロットのようになります。これは、摩擦のスケーリング係数が 1 の場合に横方向加速度が最も大きくなることを示しています。
figure for idx = 1:numExperiments % Extract Data log = get(simout(idx),'logsout'); sa=log.get('Steering-wheel angle').Values; ay=log.get('Lateral acceleration').Values; legend_labels{idx} = ['lambdamu = ', num2str(lambdamu(idx))]; % Plot steering angle vs. lateral acceleration plot(sa.Data,ay.Data) hold on end % Add labels to the plots legend(legend_labels, 'Location', 'best'); title('Lateral Acceleration') xlabel('Steering Angle [deg]') ylabel('Acceleration [m/s^2]') grid on

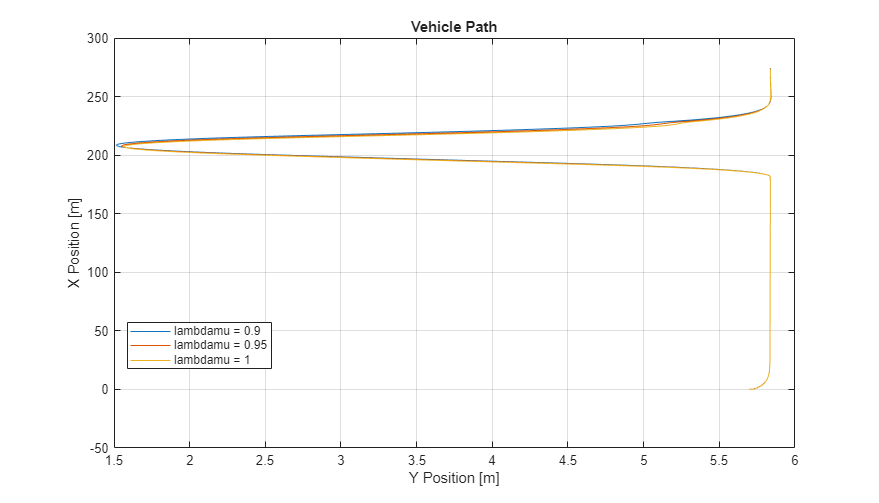
2. 車両の経路を抽出します。データをプロットします。結果は次のプロットのようになります。これは、摩擦のスケーリング係数が 0.9 の場合に車両の横方向の位置が最も大きくなることを示しています。
figure for idx = 1:numExperiments % Extract Data log = get(simout(idx),'logsout'); xValues = getSignalsByName(simoutRun(idx), 'Passenger Vehicle:1.Body.InertFrm.Cg.Disp.X').Values; yValues = getSignalsByName(simoutRun(idx), 'Passenger Vehicle:1.Body.InertFrm.Cg.Disp.Y').Values; x = xValues.Data; y = yValues.Data; legend_labels{idx} = ['lambdamu = ', num2str(lambdamu(idx))]; % Plot vehicle location plot(y,x) hold on end % Add labels to the plots legend(legend_labels, 'Location', 'best'); title('Vehicle Path') xlabel('Y Position [m]') ylabel('X Position [m]') grid on
参考
Simulink.SimulationInput | Simulink.SimulationOutput
参照
[1] ISO 3888-2: 2011. Passenger cars — Test track for a severe lane-change manoeuvre.