fitlda
Fit latent Dirichlet allocation (LDA) model
Description
A latent Dirichlet allocation (LDA) model is a topic model which discovers underlying topics in a collection of documents and infers word probabilities in topics. If the model was fit using a bag-of-n-grams model, then the software treats the n-grams as individual words.
mdl = fitlda(___,Name,Value)
Examples
To reproduce the results in this example, set rng to 'default'.
rng('default')Load the example data. The file sonnetsPreprocessed.txt contains preprocessed versions of Shakespeare's sonnets. The file contains one sonnet per line, with words separated by a space. Extract the text from sonnetsPreprocessed.txt, split the text into documents at newline characters, and then tokenize the documents.
filename = "sonnetsPreprocessed.txt";
str = extractFileText(filename);
textData = split(str,newline);
documents = tokenizedDocument(textData);Create a bag-of-words model using bagOfWords.
bag = bagOfWords(documents)
bag =
bagOfWords with properties:
Counts: [154×3092 double]
Vocabulary: ["fairest" "creatures" "desire" "increase" "thereby" "beautys" "rose" "might" "never" "die" "riper" "time" "decease" "tender" "heir" "bear" "memory" "thou" "contracted" … ]
NumWords: 3092
NumDocuments: 154
Fit an LDA model with four topics.
numTopics = 4; mdl = fitlda(bag,numTopics)
Initial topic assignments sampled in 0.263378 seconds. ===================================================================================== | Iteration | Time per | Relative | Training | Topic | Topic | | | iteration | change in | perplexity | concentration | concentration | | | (seconds) | log(L) | | | iterations | ===================================================================================== | 0 | 0.17 | | 1.215e+03 | 1.000 | 0 | | 1 | 0.02 | 1.0482e-02 | 1.128e+03 | 1.000 | 0 | | 2 | 0.02 | 1.7190e-03 | 1.115e+03 | 1.000 | 0 | | 3 | 0.01 | 4.3796e-04 | 1.118e+03 | 1.000 | 0 | | 4 | 0.01 | 9.4193e-04 | 1.111e+03 | 1.000 | 0 | | 5 | 0.01 | 3.7079e-04 | 1.108e+03 | 1.000 | 0 | | 6 | 0.01 | 9.5777e-05 | 1.107e+03 | 1.000 | 0 | =====================================================================================
mdl =
ldaModel with properties:
NumTopics: 4
WordConcentration: 1
TopicConcentration: 1
CorpusTopicProbabilities: [0.2500 0.2500 0.2500 0.2500]
DocumentTopicProbabilities: [154×4 double]
TopicWordProbabilities: [3092×4 double]
Vocabulary: ["fairest" "creatures" "desire" "increase" "thereby" "beautys" "rose" "might" "never" "die" "riper" "time" "decease" "tender" "heir" "bear" "memory" "thou" … ]
TopicOrder: 'initial-fit-probability'
FitInfo: [1×1 struct]
Visualize the topics using word clouds.
figure for topicIdx = 1:4 subplot(2,2,topicIdx) wordcloud(mdl,topicIdx); title("Topic: " + topicIdx) end
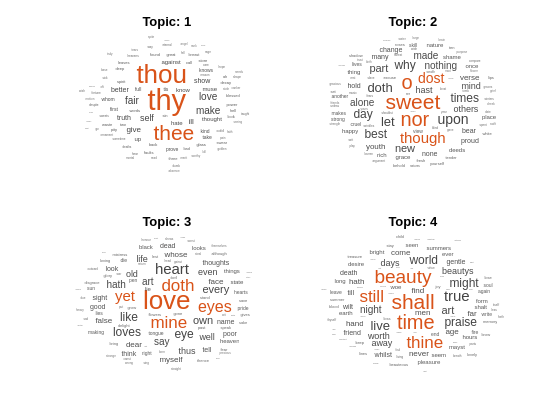
Fit an LDA model to a collection of documents represented by a word count matrix.
To reproduce the results of this example, set rng to 'default'.
rng('default')Load the example data. sonnetsCounts.mat contains a matrix of word counts and a corresponding vocabulary of preprocessed versions of Shakespeare's sonnets. The value counts(i,j) corresponds to the number of times the jth word of the vocabulary appears in the ith document.
load sonnetsCounts.mat
size(counts)ans = 1×2
154 3092
Fit an LDA model with 7 topics. To suppress the verbose output, set 'Verbose' to 0.
numTopics = 7;
mdl = fitlda(counts,numTopics,'Verbose',0);Visualize multiple topic mixtures using stacked bar charts. Visualize the topic mixtures of the first three input documents.
topicMixtures = transform(mdl,counts(1:3,:)); figure barh(topicMixtures,'stacked') xlim([0 1]) title("Topic Mixtures") xlabel("Topic Probability") ylabel("Document") legend("Topic "+ string(1:numTopics),'Location','northeastoutside')

To reproduce the results in this example, set rng to 'default'.
rng('default')Load the example data. The file sonnetsPreprocessed.txt contains preprocessed versions of Shakespeare's sonnets. The file contains one sonnet per line, with words separated by a space. Extract the text from sonnetsPreprocessed.txt, split the text into documents at newline characters, and then tokenize the documents.
filename = "sonnetsPreprocessed.txt";
str = extractFileText(filename);
textData = split(str,newline);
documents = tokenizedDocument(textData);Create a bag-of-words model using bagOfWords.
bag = bagOfWords(documents)
bag =
bagOfWords with properties:
Counts: [154×3092 double]
Vocabulary: ["fairest" "creatures" "desire" "increase" "thereby" "beautys" "rose" "might" "never" "die" "riper" "time" "decease" "tender" "heir" "bear" "memory" "thou" "contracted" … ]
NumWords: 3092
NumDocuments: 154
Fit an LDA model with 20 topics.
numTopics = 20; mdl = fitlda(bag,numTopics)
Initial topic assignments sampled in 0.513255 seconds. ===================================================================================== | Iteration | Time per | Relative | Training | Topic | Topic | | | iteration | change in | perplexity | concentration | concentration | | | (seconds) | log(L) | | | iterations | ===================================================================================== | 0 | 0.04 | | 1.159e+03 | 5.000 | 0 | | 1 | 0.05 | 5.4884e-02 | 8.028e+02 | 5.000 | 0 | | 2 | 0.04 | 4.7400e-03 | 7.778e+02 | 5.000 | 0 | | 3 | 0.04 | 3.4597e-03 | 7.602e+02 | 5.000 | 0 | | 4 | 0.03 | 3.4662e-03 | 7.430e+02 | 5.000 | 0 | | 5 | 0.03 | 2.9259e-03 | 7.288e+02 | 5.000 | 0 | | 6 | 0.03 | 6.4180e-05 | 7.291e+02 | 5.000 | 0 | =====================================================================================
mdl =
ldaModel with properties:
NumTopics: 20
WordConcentration: 1
TopicConcentration: 5
CorpusTopicProbabilities: [0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500 0.0500]
DocumentTopicProbabilities: [154×20 double]
TopicWordProbabilities: [3092×20 double]
Vocabulary: ["fairest" "creatures" "desire" "increase" "thereby" "beautys" "rose" "might" "never" "die" "riper" "time" "decease" "tender" "heir" "bear" "memory" "thou" … ]
TopicOrder: 'initial-fit-probability'
FitInfo: [1×1 struct]
Predict the top topics for an array of new documents.
newDocuments = tokenizedDocument([
"what's in a name? a rose by any other name would smell as sweet."
"if music be the food of love, play on."]);
topicIdx = predict(mdl,newDocuments)topicIdx = 2×1
19
8
Visualize the predicted topics using word clouds.
figure subplot(1,2,1) wordcloud(mdl,topicIdx(1)); title("Topic " + topicIdx(1)) subplot(1,2,2) wordcloud(mdl,topicIdx(2)); title("Topic " + topicIdx(2))
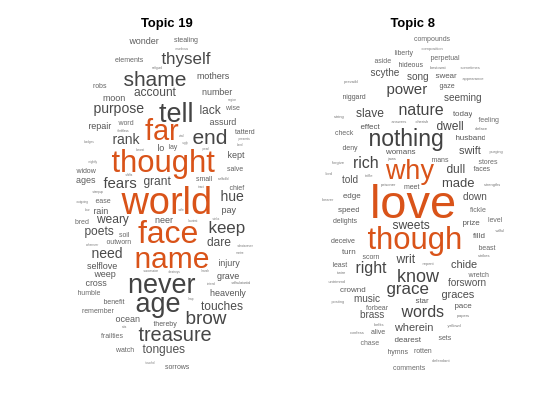
Input Arguments
Input bag-of-words or bag-of-n-grams model, specified as a bagOfWords object or a bagOfNgrams object. If bag is a
bagOfNgrams object, then the function treats each n-gram as a
single word.
Number of topics, specified as a positive integer. For an example showing how to choose the number of topics, see Choose Number of Topics for LDA Model.
Example: 200
Frequency counts of words, specified as a matrix of nonnegative integers. If you specify
'DocumentsIn' to be 'rows', then the value
counts(i,j) corresponds to the number of times the
jth word of the vocabulary appears in the ith
document. Otherwise, the value counts(i,j) corresponds to the number
of times the ith word of the vocabulary appears in the
jth document.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'Solver','avb' specifies to use approximate variational
Bayes as the solver.
Solver Options
Solver for optimization, specified as the comma-separated pair
consisting of 'Solver' and one of the following:
Stochastic Solver
Batch Solvers
'cgs'– Use collapsed Gibbs sampling [3]. This solver can be more accurate at the cost of taking longer to run. Theresumefunction does not support models fitted with CGS.'avb'– Use approximate variational Bayes [4]. This solver typically runs more quickly than collapsed Gibbs sampling and collapsed variational Bayes, but can be less accurate.'cvb0'– Use collapsed variational Bayes, zeroth order [4] [5]. This solver can be more accurate than approximate variational Bayes at the cost of taking longer to run.
For an example showing how to compare solvers, see Compare LDA Solvers.
Example: 'Solver','savb'
Relative tolerance on log-likelihood, specified as the comma-separated pair consisting
of 'LogLikelihoodTolerance' and a positive scalar. The optimization
terminates when this tolerance is reached.
Example: 'LogLikelihoodTolerance',0.001
Option for fitting topic concentration, specified as the comma-separated pair consisting of 'FitTopicConcentration' and either true or false.
The function fits the Dirichlet prior on the topic mixtures, where is the topic concentration and are the corpus topic probabilities which sum to 1.
Example: 'FitTopicProbabilities',false
Data Types: logical
Option for fitting topic concentration, specified as the comma-separated pair consisting of 'FitTopicConcentration' and either true or false.
For batch the solvers 'cgs',
'avb', and 'cvb0', the default
for FitTopicConcentration is true.
For the stochastic solver 'savb', the default is
false.
The function fits the Dirichlet prior on the topic mixtures, where is the topic concentration and are the corpus topic probabilities which sum to 1.
Example: 'FitTopicConcentration',false
Data Types: logical
Initial estimate of the topic concentration, specified as the
comma-separated pair consisting of
'InitialTopicConcentration' and a nonnegative
scalar. The function sets the concentration per topic to
TopicConcentration/NumTopics. For more
information, see Latent Dirichlet Allocation.
Example: 'InitialTopicConcentration',25
Topic order, specified as one of the following:
'initial-fit-probability'– Sort the topics by the corpus topic probabilities of input document set (theCorpusTopicProbabilitiesproperty).'unordered'– Do not sort the topics.
Word concentration, specified as the comma-separated pair consisting
of 'WordConcentration' and a nonnegative scalar. The
software sets the Dirichlet prior on the topics (the word probabilities
per topic) to be the symmetric Dirichlet distribution parameter with the
value WordConcentration/numWords, where
numWords is the vocabulary size of the input
documents. For more information, see Latent Dirichlet Allocation.
Orientation of documents in the word count matrix, specified as the comma-separated pair
consisting of 'DocumentsIn' and one of the following:
'rows'– Input is a matrix of word counts with rows corresponding to documents.'columns'– Input is a transposed matrix of word counts with columns corresponding to documents.
This option only applies if you specify the input documents as a matrix of word counts.
Note
If you orient your word count matrix so that documents correspond to columns and specify
'DocumentsIn','columns', then you might experience a significant
reduction in optimization-execution time.
Batch Solver Options
Maximum number of iterations, specified as the comma-separated pair consisting of 'IterationLimit' and a positive integer.
This option supports batch solvers only ('cgs',
'avb', or 'cvb0').
Example: 'IterationLimit',200
Stochastic Solver Options
Maximum number of passes through the data, specified as the comma-separated pair consisting of 'DataPassLimit' and a positive integer.
If you specify 'DataPassLimit' but not 'MiniBatchLimit',
then the default value of 'MiniBatchLimit' is ignored. If you specify
both 'DataPassLimit' and 'MiniBatchLimit', then
fitlda uses the argument that results in processing the fewest
observations.
This option supports only the stochastic ('savb')
solver.
Example: 'DataPassLimit',2
Maximum number of mini-batch passes, specified as the comma-separated pair consisting of 'MiniBatchLimit' and a positive integer.
If you specify 'MiniBatchLimit' but not 'DataPassLimit',
then fitlda ignores the default value of
'DataPassLimit'. If you specify both
'MiniBatchLimit' and 'DataPassLimit', then
fitlda uses the argument that results in processing the fewest
observations. The default value is ceil(numDocuments/MiniBatchSize),
where numDocuments is the number of input documents.
This option supports only the stochastic ('savb')
solver.
Example: 'MiniBatchLimit',200
Mini-batch size, specified as the comma-separated pair consisting of 'MiniBatchLimit' and a positive integer. The function processes MiniBatchSize documents in each iteration.
This option supports only the stochastic ('savb')
solver.
Example: 'MiniBatchSize',512
Learning rate decay, specified as the comma-separated pair
'LearnRateDecay' and a positive scalar less than
or equal to 1.
For mini-batch t, the function sets the learning rate to , where is the learning rate decay.
If LearnRateDecay is close to 1, then the learning
rate decays faster and the model learns mostly from the earlier
mini-batches. If LearnRateDecay is close to 0, then
the learning rate decays slower and the model continues to learn from
more mini-batches. For more information, see Stochastic Solver.
This option supports the stochastic solver only
('savb').
Example: 'LearnRateDecay',0.75
Display Options
Validation data to monitor optimization convergence, specified as the comma-separated
pair consisting of 'ValidationData' and a bagOfWords
object, a bagOfNgrams object, or a sparse matrix of word counts. If the
validation data is a matrix, then the data must have the same orientation and the same
number of words as the input documents.
Frequency of model validation in number of iterations, specified as the comma-separated pair consisting of 'ValidationFrequency' and a positive integer.
The default value depends on the solver used to fit the model. For the stochastic solver, the default value is 10. For the other solvers, the default value is 1.
Verbosity level, specified as the comma-separated pair consisting of
'Verbose' and one of the following:
0 – Do not display verbose output.
1 – Display progress information.
Example: 'Verbose',0
Output Arguments
Output LDA model, returned as an ldaModel object.
More About
A latent Dirichlet allocation (LDA) model is a document topic model which discovers underlying topics in a collection of documents and infers word probabilities in topics. LDA models a collection of D documents as topic mixtures , over K topics characterized by vectors of word probabilities . The model assumes that the topic mixtures , and the topics follow a Dirichlet distribution with concentration parameters and respectively.
The topic mixtures are probability vectors of length K, where
K is the number of topics. The entry is the probability of topic i appearing in the
dth document. The topic mixtures correspond to the rows of the
DocumentTopicProbabilities property of the ldaModel
object.
The topics are probability vectors of length V, where
V is the number of words in the vocabulary. The entry corresponds to the probability of the vth word of the
vocabulary appearing in the ith topic. The topics correspond to the columns of the TopicWordProbabilities
property of the ldaModel object.
Given the topics and Dirichlet prior on the topic mixtures, LDA assumes the following generative process for a document:
Sample a topic mixture . The random variable is a probability vector of length K, where K is the number of topics.
For each word in the document:
Sample a topic index . The random variable z is an integer from 1 through K, where K is the number of topics.
Sample a word . The random variable w is an integer from 1 through V, where V is the number of words in the vocabulary, and represents the corresponding word in the vocabulary.
Under this generative process, the joint distribution of a document with words , with topic mixture , and with topic indices is given by
where N is the number of words in the document. Summing the joint distribution over z and then integrating over yields the marginal distribution of a document w:
The following diagram illustrates the LDA model as a probabilistic graphical model. Shaded nodes are observed variables, unshaded nodes are latent variables, nodes without outlines are the model parameters. The arrows highlight dependencies between random variables and the plates indicate repeated nodes.

The Dirichlet distribution is a continuous generalization of the multinomial distribution. Given the number of categories , and concentration parameter , where is a vector of positive reals of length K, the probability density function of the Dirichlet distribution is given by
where B denotes the multivariate Beta function given by
A special case of the Dirichlet distribution is the symmetric Dirichlet distribution. The symmetric Dirichlet distribution is characterized by the concentration parameter , where all the elements of are the same.
The stochastic solver processes documents in mini-batches. It updates the per-topic word probabilities using a weighted sum of the probabilities calculated from each mini-batch, and the probabilities from all previous mini-batches.
For mini-batch t, the solver sets the learning rate to , where is the learning rate decay.
The function uses the learning rate decay to update , the matrix of word probabilities per topic, by setting
where is the matrix learned from mini-batch t, and is the matrix learned from mini-batches 1 through t-1.
Before learning begins (when t = 0), the function initializes the initial word probabilities per topic with random values.
References
[1] Foulds, James, Levi Boyles, Christopher DuBois, Padhraic Smyth, and Max Welling. "Stochastic collapsed variational Bayesian inference for latent Dirichlet allocation." In Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining, pp. 446–454. ACM, 2013.
[2] Hoffman, Matthew D., David M. Blei, Chong Wang, and John Paisley. "Stochastic variational inference." The Journal of Machine Learning Research 14, no. 1 (2013): 1303–1347.
[3] Griffiths, Thomas L., and Mark Steyvers. "Finding scientific topics." Proceedings of the National academy of Sciences 101, no. suppl 1 (2004): 5228–5235.
[4] Asuncion, Arthur, Max Welling, Padhraic Smyth, and Yee Whye Teh. "On smoothing and inference for topic models." In Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence, pp. 27–34. AUAI Press, 2009.
[5] Teh, Yee W., David Newman, and Max Welling. "A collapsed variational Bayesian inference algorithm for latent Dirichlet allocation." In Advances in neural information processing systems, pp. 1353–1360. 2007.
Version History
Introduced in R2017bStarting in R2018b, fitlda, by default, sorts the topics in
descending order of the topic probabilities of the input document set. This behavior
makes it easier to find the topics with the highest probabilities.
In previous versions, fitlda does not change the topic order.
To reproduce the behavior, set the 'TopicOrder' option to 'unordered'.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)