acos
シンボリック逆余弦関数
構文
説明
例
数値引数およびシンボリック引数に対する逆余弦関数
引数に応じて、acos は浮動小数点解またはシンボリック厳密解の結果を返します。
次の数値について逆余弦関数を計算します。これらの数値はシンボリック オブジェクトではないため、acos は浮動小数点の結果を返します。
A = acos([-1, -1/3, -1/2, 1/4, 1/2, sqrt(3)/2, 1])
A =
3.1416 1.9106 2.0944 1.3181 1.0472 0.5236 0シンボリック オブジェクトに変換された数値の逆余弦関数を計算します。ほとんどのシンボリックな (厳密な) 数値に対して、acos は未解決のシンボリックな呼び出しを返します。
symA = acos(sym([-1, -1/3, -1/2, 1/4, 1/2, sqrt(3)/2, 1]))
symA = [ pi, pi - acos(1/3), (2*pi)/3, acos(1/4), pi/3, pi/6, 0]
vpa を使用し、これらの解を浮動小数点数で近似します。
vpa(symA)
ans = [ 3.1415926535897932384626433832795,... 1.9106332362490185563277142050315,... 2.0943951023931954923084289221863,... 1.318116071652817965745664254646,... 1.0471975511965977461542144610932,... 0.52359877559829887307710723054658,... 0]
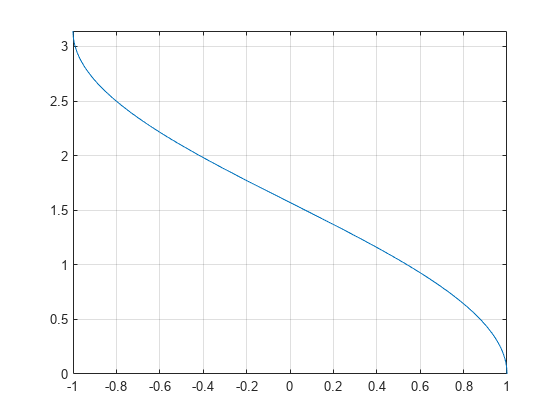
逆余弦関数のプロット
逆コサイン関数を -1 から 1 までの範囲でプロットします。
syms x fplot(acos(x),[-1 1]) grid on
逆余弦関数を含む式の処理
diff、int、taylor、rewrite などの多くの関数は acos を含む式を処理することができます。
逆余弦関数の 1 次および 2 次導関数を求めます。
syms x diff(acos(x), x) diff(acos(x), x, x)
ans = -1/(1 - x^2)^(1/2) ans = -x/(1 - x^2)^(3/2)
逆余弦関数の不定積分を求めます。
int(acos(x), x)
ans = x*acos(x) - (1 - x^2)^(1/2)
acos(x) のテイラー級数展開を計算します。
taylor(acos(x), x)
ans = - (3*x^5)/40 - x^3/6 - x + pi/2
逆余弦関数を自然対数に書き換えます。
rewrite(acos(x), 'log')
ans = -log(x + (1 - x^2)^(1/2)*1i)*1i
入力引数
バージョン履歴
R2006a より前に導入