微分

この例では、Symbolic Math Toolbox™ を使って微分を求める方法を説明します。

最初に、シンボリック式を作成します。

syms x
f = sin(5*x);

式 f を x について微分します。

Df = diff(f)

Df =  $5 \cos (5 x)$

他の例として、exp(x) を使用して $e^{x}$ を表す別の式を指定します。

g = exp(x)*cos(x);

式 g を微分します。

y = diff(g)

y =  $e^{x} \cos (x) - e^{x} \sin (x)$

与えられた値 x について g の微分を求めるには、subs を使用して x をその値に置き換え、vpa を使用して数値を返します。x = 2 における g の微分を求めます。

y_eval = vpa(subs(y,x,2))

y_eval =  $- 9.7937820180676088383807818261614$

g の 2 次導関数を計算するために、diff(g,2) を使用します。

D2g = diff(g,2)

D2g =  $- 2 e^{x} \sin (x)$

この微分を 2 回計算しても、同じ結果を得ることができます。

D2g = diff(diff(g))

D2g =  $- 2 e^{x} \sin (x)$

この例では、Symbolic Math Toolbox は単純化した解を返します。しかし、解が単純化されない場合もあり、その場合は simplify コマンドを使用できます。この例の次のセクションでは、このような単純化を行うケースについて説明します。

定数を微分する場合、まず定数をシンボリック式として定義しなければならないことに注意してください。

c = sym("5");
Dc = diff(c)

Dc =  $0$

diff を 5 などの定数に直接使用する場合、その定数はシンボリックオブジェクトではなく double 数値型であるため、結果は空の配列になります。

Dc = diff(5)

Dc =

     []

複数の変数からなる式の微分

複数のシンボリック変数からなる式を微分するには、どの変数で微分するかを設定します。その後、diff コマンドはその変数で式の偏微分を計算します。たとえば、2 変数をもつシンボリック式を指定します。

syms s t
f = sin(s*t);

diff を使用して、微分する変数を t として指定することで、偏微分 $\partial f / \partial t$ を求めます。

Df_t = diff(f,t)

Df_t =  $s \cos (s t)$

f を変数 s で微分するには、微分する変数を s として指定します。

Df_s = diff(f,s)

Df_s =  $t \cos (s t)$

どの変数で微分するかを指定しない場合、diff は既定の変数を使用します。既定の変数はアルファベット順で x に最も近い文字になるのが規則です。一連の規則については、式、関数、および行列でのシンボリック変数の検索を参照してください。前の例を考えると、diff(f) は、f を t で微分します。これは、t が s よりもアルファベット上で x に近い位置に存在するからです。MATLAB® が微分する既定の変数を確認するには、symvarを使います。

fvar = symvar(f,1)

fvar =  $t$

t について f の 2 次導関数を計算します。

D2f = diff(f,t,2)

D2f =  $- s^{2} \sin (s t)$

t が既定の変数であるため、diff(f,2) によっても同じ解が返されることに注意してください。

微分に関するその他の例

他の式に対する diff 関数について詳しく説明するため、シンボリック変数 a、b、x、n、t、および theta を定義します。

syms a b x n t theta

以下の表は、他のいくつかの式に diff を使用した結果について説明しています。

`f`	`diff(f)`
`>> syms x n` `>> f = x^n;`	`>> Df = diff(f)` `Df =` `n*x^(n - 1)`
`>> syms a b t` `>> f = sin(a*t + b);`	`>> Df = diff(f)` `Df =` `acos(b + at)`
`>> syms theta` `>> f = exp(i*theta);`	`>> Df = diff(f)` `Df =` `exp(theta1i)1i`

f

diff(f)

>> syms x n

>> f = x^n;

>> Df = diff(f)

Df =

n*x^(n - 1)

>> syms a b t

>> f = sin(a*t + b);

>> Df = diff(f)

Df =

a*cos(b + a*t)

>> syms theta

>> f = exp(i*theta);

>> Df = diff(f)

Df =

exp(theta*1i)*1i

第 1 種ベッセル関数 besselj(nu,z) を z について微分できます。

syms nu z
b = besselj(nu,z);
Db = diff(b)

Db = 
 $\frac{ν {J besselj}_{ν} (z)}{z} - {J besselj}_{ν + 1} (z)$

diff 関数は、その入力としてシンボリック行列を与えることもできます。この場合、微分は要素単位に行われます。

syms a x
A = [cos(a*x),sin(a*x);-sin(a*x),cos(a*x)]

A = 
 $(\begin{array}{c} \cos (a x) & \sin (a x) \\ - \sin (a x) & \cos (a x) \end{array})$

x について A の微分を求めます。

DA = diff(A)

DA = 
 $(\begin{array}{c} - a \sin (a x) & a \cos (a x) \\ - a \cos (a x) & - a \sin (a x) \end{array})$

ベクトルの引数についてベクトル関数の微分を実行することもできます。直交座標 $(x, y, z)$ から次で与えられる球面座標 $(r, λ, φ)$ に変換することを考えます。

$x = r \cos λ \cos φ$ ,

$y = r \cos λ \sin φ$ ,

$z = r \sin λ$ .

ここで、 $λ$ は仰角または緯度に相当し、 $φ$ は方位角または経度に相当します。

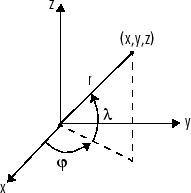
A point in 3-D space can be represented in Cartesian coordinates (x,y,z) or spherical coordinates (r,lambda,phi)

この変換のヤコビ行列 $J$ を計算するために、jacobian 関数を使います。 $J$ を数学的に表記します。

$J = \frac{\partial (x, y, z)}{\partial (r, λ, φ)}$ .

ヤコビアンを計算するために、l を使用して $λ$ を表し、f を使用して $φ$ を表します。ヤコビアンを求めます。

syms r l f
x = r*cos(l)*cos(f);
y = r*cos(l)*sin(f);
z = r*sin(l);
J = jacobian([x; y; z], [r l f])

J = 
 $(\begin{array}{c} \cos (f) \cos (l) & - r \cos (f) \sin (l) & - r \cos (l) \sin (f) \\ \cos (l) \sin (f) & - r \sin (f) \sin (l) & r \cos (f) \cos (l) \\ \sin (l) & r \cos (l) & 0 \end{array})$

このヤコビアンの行列式を求め、結果を単純化します。

detJ = simplify(det(J))

detJ =  $- r^{2} \cos (l)$

jacobian関数の引数は列ベクトルまたは行ベクトルです。また、ヤコビアンの行列式はかなり複雑な三角関数式なので、simplifyを使って三角関数の置換や簡約 (単純化) が可能です。

次の表は、diff および jacobian をまとめています。

数学演算子	Symbolic Math Toolbox を使用したコマンド
$\frac{d f}{d x}$	`diff(f)` または `diff(f,x)`
$\frac{d f}{d a}$	`diff(f,a)`
$\frac{d^{2} f}{d b^{2}}$	`diff(f,b,2)`
$J = \frac{\partial (r, t)}{\partial (u, v)}$	`J = jacobian([r; t],[u; v])`

参考

外部の Web サイト

Calculus Derivatives (MathWorks Teaching Resources)