このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

functionalDerivative

汎関数微分 (変分導関数)

構文

G = functionalDerivative(f,y)

説明

G = functionalDerivative(f,y) は、汎関数 $$S\left[y\right]={\displaystyle {\int }_a^{b}f\left[x,y\left(x\right),y\text{'}\left(x\right),\mathrm{...}\right]dx}$$ の関数 y = y(x) に対する汎関数微分 $$\frac{\delta S}{\delta y}\left(x\right)$$ を返します。ここで、x は 1 つ以上の独立変数です。汎関数微分は、y(x) の微小な変動に対する汎関数 S[y] の変化に関連しています。汎関数微分は変分導関数としても知られています。

y がシンボリック関数のベクトルの場合、functionalDerivative は y の関数に対する汎関数微分のベクトルを返します。ここで、y のすべての関数は同じ独立変数に従属する必要があります。

例

単一の関数に対する汎関数微分

汎関数 $$S[y]={\int }_b^{a}y(x)\sin (y(x))dx$$ の関数 $$y$$ に対する汎関数微分を求めます。ここで、被積分は $$f[y(x)]=y(x)\sin (y(x))$$ です。

y(x) をシンボリック関数として宣言し、f を $$S$$ の被積分として定義します。f と y を functionalDerivative のパラメーターとして使用します。

syms y(x)
f = y*sin(y);
G = functionalDerivative(f,y)

G(x) = $$\sin \left(y\left(x\right)\right)+\cos \left(y\left(x\right)\right)\hspace{0.17em}y\left(x\right)$$

2 つの関数に対する汎関数微分

汎関数 $$S[u,v]={\displaystyle {\int }_b^a(u^2(x)\frac{dv(x)}{dx}+v(x)\frac{d^{2}u(x)}{d{x}^2})dx}$$ の関数 $$u$$ および $$v$$ に対する汎関数微分を求めます。ここで、被積分は $$f[u(x),v(x),u^{\prime \prime }(x),v^{\prime }(x)]=u^2\frac{dv}{dx}+v\frac{d^{2}u}{d{x}^2}$$ です。

u(x) と v(x) をシンボリック関数として宣言し、f を $$S$$ の被積分として定義します。

syms u(x) v(x)
f = u^2*diff(v,x) + v*diff(u,x,x);

シンボリック関数 [u v] のベクトルを、functionalDerivative の 2 番目の入力引数として指定します。

G = functionalDerivative(f,[u v])

G(x) = 
$$\left(\begin{array}{c}\frac{{\partial }^2}{\partial x^2}\mathrm{ }v\left(x\right)+2\hspace{0.17em}u\left(x\right)\hspace{0.17em}\frac{\partial }{\partial x}\mathrm{ }v\left(x\right)\\ \frac{{\partial }^2}{\partial x^2}\mathrm{ }u\left(x\right)-2\hspace{0.17em}u\left(x\right)\hspace{0.17em}\frac{\partial }{\partial x}\mathrm{ }u\left(x\right)\end{array}\right)$$

functionalDerivative は、被積分 f の u および v それぞれに対する汎関数微分を含むシンボリック関数のベクトルを返します。

単純なバネ質量系のオイラー・ラグランジュ方程式

バネ定数 k のバネに接続されている重り m のオイラー・ラグランジュ方程式を求めます。

系の運動エネルギー T、位置エネルギー V、およびラグランジュ関数 L を定義します。ラグランジュ関数は、運動エネルギーと位置エネルギーの差です。

syms m k x(t)
T = 1/2*m*diff(x,t)^2;
V = 1/2*k*x^2;
L = T - V

L(t) = 
$$\frac{m\hspace{0.17em}{\left(\frac{\partial }{\partial t}\mathrm{ }x\left(t\right)\right)}^2}{2}-\frac{k\hspace{0.17em}{x\left(t\right)}^2}{2}$$

ラグランジュ力学では、系の作用汎関数は、時間の経過に伴うラグランジュ関数の積分に等しくなります ($$S[x]={\int }_{t_1}^{t_2}L[t,x(t),\underset{}{\overset{\dot{}}{x}}(t)]dt$$)。オイラー・ラグランジュ方程式は、$$S[x(t)]$$ が定常である系の運動を表します。

被積分 L の汎関数微分を取って、それを 0 に設定することにより、オイラー・ラグランジュ方程式を求めます。

eqn = functionalDerivative(L,x) == 0

eqn(t) = 
$$-m\hspace{0.17em}\frac{{\partial }^2}{\partial t^2}\mathrm{ }x\left(t\right)-k\hspace{0.17em}x\left(t\right)=0$$

eqn は、バネ質量系の振動を表す微分方程式です。

dsolve を使用して、eqn の解を求めます。質量 m とバネ定数 k は正であると仮定します。振動振幅の初期条件を $$x(0)=10$$ に、重りの初期速度を $$\underset{}{\overset{\dot{}}{x}}(0)=0$$ に設定します。

assume(m,'positive')
assume(k,'positive')
Dx(t) = diff(x(t),t);
xSol = dsolve(eqn,[x(0) == 10, Dx(0) == 0])

xSol = 
$$10\hspace{0.17em}\cos \left(\frac{\sqrt{k}\hspace{0.17em}t}{\sqrt{m}}\right)$$

計算を続けるため、仮定を消去します。

assume([k m],'clear')

最速降下問題の微分方程式

最速降下問題は、摩擦のない重力下における粒子の最短の降下経路を見つける問題です。運動は垂直面に限定されます。重力 $$g$$ の下で、曲線 $$y(x)$$ に沿って $$a$$ から $$b$$ へ動く物体の時間は、次式で与えられます。

$$t={\int }_a^b\sqrt{\frac{1+{y^{\prime }}^2}{2gy}}dx.$$

経路 $$y$$ の微小な変動に対する $$t$$ の変化を最小にすることによって、最速経路を求めます。最小にするための条件は、$$\frac{\delta t}{\delta y}(x)=0$$ です。

この汎関数微分を計算して、最速降下問題を記述する微分方程式を求めます。simplify を使用して方程式を単純化し、想定される形式にします。

syms g y(x)
assume(g,'positive')
f = sqrt((1 + diff(y)^2)/(2*g*y));
eqn = functionalDerivative(f,y) == 0;
eqn = simplify(eqn)

eqn(x) = 
$$2\hspace{0.17em}y\left(x\right)\hspace{0.17em}\frac{{\partial }^2}{\partial x^2}\mathrm{ }y\left(x\right)+{\left(\frac{\partial }{\partial x}\mathrm{ }y\left(x\right)\right)}^2=-1$$

この方程式は、最速降下問題の標準の微分方程式です。微分方程式の解を見つけるには、dsolve を使用します。'Implicit' オプションを true に指定して、$$F(y(x))=g(x)$$ の形式を取る陰的な解を返します。

sols = dsolve(eqn,'Implicit',true)

sols = 
$$\begin{array}{l}\left(\begin{array}{c}y\left(x\right)=C_5+x\hspace{0.17em}\mathrm{i}\\ y\left(x\right)=C_4-x\hspace{0.17em}\mathrm{i}\\ {\sigma }_1=C_3-x\\ \frac{C_1+y\left(x\right)}{y\left(x\right)}=0\\ {\sigma }_1=C_2+x\end{array}\right)\\ \\ \mathrm{where}\\ \\ \mathrm{ }{\sigma }_1=C_1\hspace{0.17em}\mathrm{atan}\left(\sqrt{-\frac{C_1}{y\left(x\right)}-1}\right)-y\left(x\right)\hspace{0.17em}\sqrt{-\frac{C_1}{y\left(x\right)}-1}\end{array}$$

シンボリック ソルバー dsolve は複素空間での一般解を返します。Symbolic Math Toolbox™ は、シンボリック関数 $$y(x)$$ が実数であるとの仮定を受け入れません。

境界条件に応じて、この最速降下問題に対する 2 つの実空間の解があります。以下の 2 つの解のうち一方が実空間でのサイクロイド曲線を表します。

solCycloid1 = sols(3)

solCycloid1 = 
$$C_1\hspace{0.17em}\mathrm{atan}\left(\sqrt{-\frac{C_1}{y\left(x\right)}-1}\right)-y\left(x\right)\hspace{0.17em}\sqrt{-\frac{C_1}{y\left(x\right)}-1}=C_3-x$$

solCycloid2 = sols(5)

solCycloid2 = 
$$C_1\hspace{0.17em}\mathrm{atan}\left(\sqrt{-\frac{C_1}{y\left(x\right)}-1}\right)-y\left(x\right)\hspace{0.17em}\sqrt{-\frac{C_1}{y\left(x\right)}-1}=C_2+x$$

実空間での別の解は、水平直線です。ここで $$y$$ は定数です。

solStraight = simplify(sols(4))

solStraight = $$C_1+y\left(x\right)=0$$

サイクロイドの解について説明するため、境界条件 $$y(0)=5$$ および $$y(4)=1$$ での例を考えます。この場合、与えられた境界条件を満たすことができる方程式は solCycloid1 です。2 つの境界条件を solCycloid1 に代入します。

eq1 = subs(solCycloid1,[x y(x)],[0 5]);
eq2 = subs(solCycloid1,[x y(x)],[4 1]);

2 つの方程式 eq1、eq2 には 2 つの未知の係数 $$C_1$$、$$C_3$$ があります。vpasolve を使用して、係数の数値解を求めます。それらの解を solCycloid1 に代入します。

coeffs = vpasolve([eq1 eq2]);
eqCycloid = subs(solCycloid1,{'C1','C3'},{coeffs.C1,coeffs.C3})

eqCycloid = 
$$-6.4199192418473511250705556729108\hspace{0.17em}\mathrm{atan}\left(\sqrt{\frac{6.4199192418473511250705556729108}{y\left(x\right)}-1}\right)-y\left(x\right)\hspace{0.17em}\sqrt{\frac{6.4199192418473511250705556729108}{y\left(x\right)}-1}=-x-5.8078336827583088482183433150164$$

陰的方程式 eqCycloid は、$$x$$ と $$y(x)$$ に関する最速降下問題のサイクロイドの解を表します。

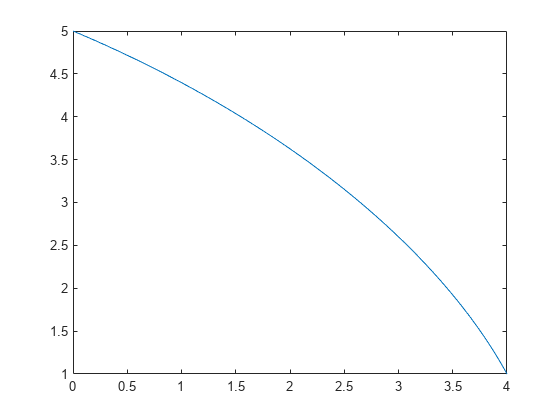
次に、fimplicit を使用して eqCycloid をプロットできます。fimplicit はシンボリック変数 $$x$$ および $$y$$ を含む陰的なシンボリック方程式のみを受け入れるため、シンボリック関数 $$y(x)$$ をシンボリック変数 $$y$$ に変換します。mapSymType を使用して、$$y(x)$$ を $$y$$ に変換します。境界条件 $$0<x<4$$ および $$1<y<5$$ の範囲でサイクロイドの解をプロットします。

funToVar = @(obj) sym('y');
eqPlot = mapSymType(eqCycloid,'symfun',funToVar);
fimplicit(eqPlot,[0 4 1 5])

3 次元空間での極小表面方程式

3 次元空間の表面を表す関数 $$u(x,y)$$ の表面積は次の汎関数で求めることができます。

$$F[u]={\int }_{y_1}^{y_2}{\int }_{x_1}^{x_2}f[x,y(x),u(x,y),u_x,u_y]dxdy={\int }_{y_1}^{y_2}{\int }_{x_1}^{x_2}\sqrt{1+u_x^2+u_y^2}dxdy$$

ここで $$u_x$$ および $$u_y$$ は $$x$$ と $$y$$ に対する $$u$$ の偏導関数です。

被積分 f の汎関数微分を、u について求めます。

syms u(x,y)
f = sqrt(1 + diff(u,x)^2 + diff(u,y)^2);
G = functionalDerivative(f,u)

G(x, y) = 
$$\begin{array}{l}-\frac{{\left(\frac{\partial }{\partial y}\mathrm{ }u\left(x,y\right)\right)}^2\hspace{0.17em}\frac{{\partial }^2}{\partial x^2}\mathrm{ }u\left(x,y\right)+\frac{{\partial }^2}{\partial x^2}\mathrm{ }u\left(x,y\right)+{{\sigma }_1}^2\hspace{0.17em}\frac{{\partial }^2}{\partial y^2}\mathrm{ }u\left(x,y\right)-2\hspace{0.17em}\frac{\partial }{\partial y}\mathrm{ }{\sigma }_1\hspace{0.17em}\frac{\partial }{\partial y}\mathrm{ }u\left(x,y\right)\hspace{0.17em}{\sigma }_1+\frac{{\partial }^2}{\partial y^2}\mathrm{ }u\left(x,y\right)}{{\left({{\sigma }_1}^2+{\left(\frac{\partial }{\partial y}\mathrm{ }u\left(x,y\right)\right)}^2+1\right)}^{3/2}}\\ \\ \mathrm{where}\\ \\ \mathrm{ }{\sigma }_1=\frac{\partial }{\partial x}\mathrm{ }u\left(x,y\right)\end{array}$$

結果は、u(x,y) で定義される 3 次元表面の極小表面を表す方程式 G です。この方程式の解は、シャボン玉のような 3 次元空間の極小表面を示しています。

入力引数

f — 汎関数の被積分

シンボリック変数 | シンボリック関数 | シンボリック式

汎関数の被積分。シンボリック変数、シンボリック関数、またはシンボリック式として指定します。引数 f は汎関数の密度を表します。

y — 微分関数

未割り当てのシンボリック関数 | 未割り当てのシンボリック関数のベクトル | 未割り当てのシンボリック関数の行列 | 未割り当てのシンボリック関数の多次元配列

微分関数。未割り当てのシンボリック関数として指定するか、未割り当てのシンボリック関数から成るベクトル、行列、または多次元配列として指定します。引数 y は、1 つ以上の独立変数の関数の場合があります。y がシンボリック関数のベクトルの場合、functionalDerivative は y の関数に対する汎関数微分のベクトルを返します。ここで、y のすべての関数は同じ独立変数に従属する必要があります。

例: syms y(x); G = functionalDerivative(y*sin(y),y)

出力引数

G — 汎関数微分

シンボリック関数 | シンボリック関数のベクトル

シンボリック関数またはシンボリック関数からなるベクトルとして返された汎関数微分。入力 y がベクトル、行列、または配列の場合、G はベクトルです。

詳細

汎関数微分

次の汎関数を考えます。

$$S\left[y\right]={\displaystyle {\int }_a^{b}f\left[x,y\left(x\right),y\text{'}\left(x\right),\mathrm{...},y^{(n)}\left(x\right)\right]dx},$$

ここで、x 空間における a から b までの経路は任意であるとします。

経路 y(x) の微小な変動に対して、変化を $$\delta y(x)=\epsilon \varphi (x)$$ として定義します。ここで、ϕ(x) は任意のテスト関数です。汎関数 S の変化は次のようになります。

$$DS\left[y\right]=\underset{\epsilon \to 0}{\lim }\frac{S\left[y+\epsilon \varphi \right]-S\left[y\right]}{\epsilon }={\displaystyle {\int }_a^b\frac{\delta S}{\delta y}\left(x\right)\varphi (x)dx}\text{.}$$

式 $$\frac{\delta S}{\delta y}\left(x\right)$$ は y に対する S の汎関数微分です。線形汎関数 DS[y] は、汎関数 S の第 1 変分またはガトー微分としても知られています。

汎関数微分を計算する 1 つの方法は、ε についての方程式 S[y + εϕ] にテイラー展開を適用することです。1 次項は ε のままで、部分積分を実行し、境界条件 ϕ(a) = ϕ(b) = ϕ'(a) = ϕ'(b) = ... = 0 を選択すると、汎関数微分は次のようになります。

$$\begin{array}{lll}\frac{\delta S}{\delta y}\left(x\right)\hfill & =\hfill & \frac{\partial f}{\partial y}-\frac{d}{dx}\frac{\partial f}{\partial y^{\text{'}}}+\frac{d^2}{d{x}^2}\frac{\partial f}{\partial y^{\text{'}\text{'}}}-\mathrm{...}+{\left(-1\right)}^n\frac{d^n}{d{x}^n}\left(\frac{\partial f}{\partial y^{(n)}}\right)\hfill \\ \hfill & =\hfill & {\displaystyle \sum _{i=0}^n{\left(-1\right)}^i\frac{d^i}{d{x}^i}\left(\frac{\partial f}{\partial y^{(i)}}\right)}.\hfill \end{array}$$

バージョン履歴

R2015a で導入

参考

diff | dsolve | int

トピック

• 汎関数微分のチュートリアル