Symbolic Math Toolbox の計算数学

変数、式、関数および方程式

MATLAB® の変数は、既定では倍精度です。Symbolic Math Toolbox はこれを拡張し、sym の使用と vpa による可変精度の使用によって、厳密なシンボリック形式で数値を表現できるようにしています。

pi/6 + pi/4

ans = 1.3090

sym(pi/6) + sym(pi/4)

ans = 
$$\frac{5\hspace{0.17em}\pi }{12}$$

vpa(pi/6) + vpa(pi/4)

ans = $$1.3089969389957471826927680763665$$

シンボリック変数は、三角関数、対数関数、指数関数、特殊関数などの数式、関数および方程式で使用できます。シンボリック式を作成し、その数学演算を実行できます。

syms x y 
log(x) + exp(y)

ans = $${\mathrm{e}}^y+\log \left(x\right)$$

区分的関数を作成することもできます。

y(x) = piecewise(x<0, -1, x>0, 1)

y(x) = 
$$\{\begin{array}{cl}-1& \text{ if }x<0\\ 1& \text{ if }0<x\end{array}$$

シンボリック関数の作成を作成して評価します。$$x=-5$$ における f の値を求めます。

syms f(x)
f(x) = x^4-2*x^3+6*x^2-2*x+10

f(x) = $$x^4-2\hspace{0.17em}{x}^3+6\hspace{0.17em}{x}^2-2\hspace{0.17em}x+10$$

f(-5)

ans = $$1045$$

solve を使い、線 $$y1$$ と $$y2$$ の共通部分を求めます。== 演算子を使用して線を等式化します。

syms y1 y2
y1 = x+3; y2 = 3*x;
solve(y1 == y2)

ans = 
$$\frac{3}{2}$$

シンボリック変数のassumeを設定します。$$x^4=1$$ の解は 4 つ (2 つの実数と 2 つの複素数) あります。$$x$$ が実数で、かつ $$x>0$$ と仮定すると、解は 1 つだけ存在します。

syms x
solve(x^4 == 1)

ans = 
$$\left(\begin{array}{c}-1\\ 1\\ -\mathrm{i}\\ \mathrm{i}\end{array}\right)$$

assume(x,'real')
assumeAlso( x > 0)
assumptions(x)

ans = $$\left(\begin{array}{cc}x\in \mathbb{R}& 0<x\end{array}\right)$$

solve(x^4 == 1)

ans = $$1$$

assume(x,'clear')

代入と求解

Symbolic Math Toolbox では、subs を使用して式の一部に代入することにより、数学関数の評価をサポートします。数値、他のシンボリック変数やシンボリック式、ベクトルまたは行列のいずれかを代入できます。Symbolic Math Toolbox では、solve を使用して方程式と方程式系の求解をサポートします。多変数方程式の求解、不等式の求解および仮定を使用した求解をサポートします。可変精度の演算を使用して、シンボリックまたは数値的に解を高精度に求めることができます。

シンボリック変数を使用して代入を行います。$$x=xo-1$$ を $$x^2+1$$ に代入します。

syms x xo
subs(x^2+1,x,xo-1)

ans = $${\left(\mathrm{xo}-1\right)}^2+1$$

複数の値を代入します。たとえば、$$a=\frac{\pi }{2},b=\frac{\pi }{4},c=-1$$ を代入して $$cos(a)+sin(b)-e^{2C}$$ を評価します。

syms a b c
subs(cos(a) + sin(b) - exp(2*c), [a b c], [pi/2 pi/4 -1])

ans = 
$$\frac{\sqrt{2}}{2}-{\mathrm{e}}^{-2}$$

方程式を作成して解きます。$$9x^2-1=0$$ の零点を求めます。

solve(9*x^2 - 1 == 0)

ans = 
$$\left(\begin{array}{c}-\frac{1}{3}\\ \frac{1}{3}\end{array}\right)$$

一般的な 2 次方程式 $$a{x}^2+bx+c=0$$ を解き、subs を使用して、その解を$$a=9,b=0,c=-1$$ について評価します。

eqn = a*x^2 + b*x + c == 0;
sol = solve(eqn) 

sol = 
$$\left(\begin{array}{c}-\frac{b+\sqrt{b^2-4\hspace{0.17em}a\hspace{0.17em}c}}{2\hspace{0.17em}a}\\ -\frac{b-\sqrt{b^2-4\hspace{0.17em}a\hspace{0.17em}c}}{2\hspace{0.17em}a}\end{array}\right)$$

subs(sol,[a b c],[9 0 -1])

ans = 
$$\left(\begin{array}{c}-\frac{1}{3}\\ \frac{1}{3}\end{array}\right)$$

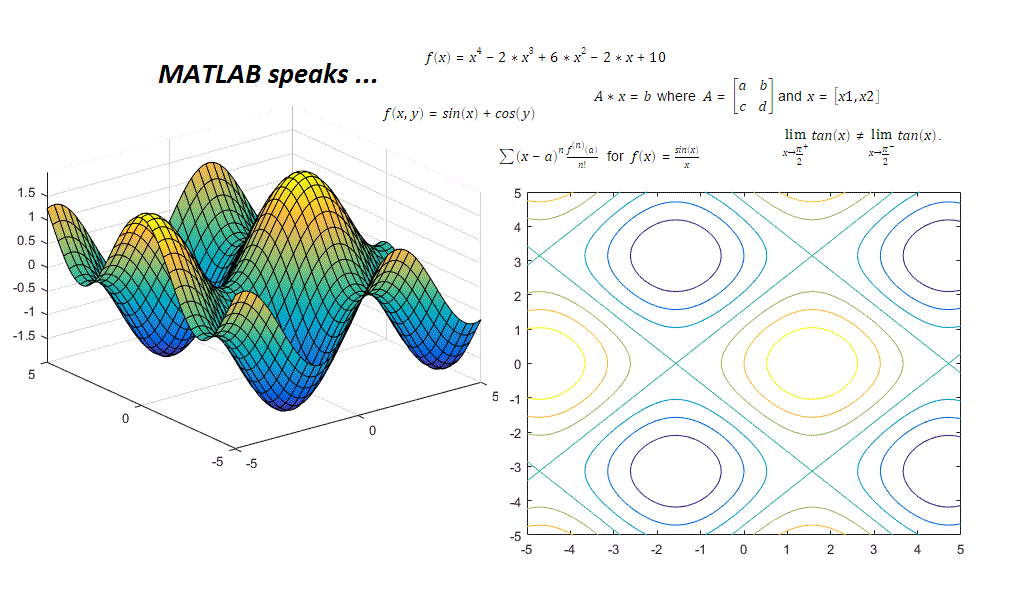
厳密な結果や高い精度が必要な場合、方程式を、シンボリックに解くか、可変精度の演算を使用して解きます。$\mathit{f}\left(\mathit{x}\right)=6{\mathit{x}}^7-2{\mathit{x}}^6+3{\mathit{x}}^3-8$ のグラフはその根の周辺で非常にフラットになっています。

syms x f(x)
assume(x>0)
f(x) = 6*x^7-2*x^6+3*x^3-8;
fplot(f)
xlim([-10 10])
ylim([-1e3 1e3])

doubleSol = roots([6 -2 0 0 3 0 0 -8]) %  double-precision

doubleSol = 7×1 complex

   1.0240 + 0.0000i
   0.7652 + 0.8319i
   0.7652 - 0.8319i
  -0.8808 + 0.5043i
  -0.8808 - 0.5043i
  -0.2297 + 0.9677i
  -0.2297 - 0.9677i

symsSol = solve(f) % exact. The roots object stores the zeros for symbolic computations

symsSol = 
$$\mathrm{root}\left(z^7-\frac{z^6}{3}+\frac{z^3}{2}-\frac{4}{3},z,5\right)$$

vpaSol = vpasolve(f) % variable-precision 

vpaSol = 
$$\left(\begin{array}{c}1.0240240759053702941448316563337\\ -0.88080620051762149639205672298326+0.50434058840127584376331806592405\hspace{0.17em}\mathrm{i}\\ -0.88080620051762149639205672298326-0.50434058840127584376331806592405\hspace{0.17em}\mathrm{i}\\ -0.22974795226118163963098570610724+0.96774615576744031073999010695171\hspace{0.17em}\mathrm{i}\\ -0.22974795226118163963098570610724-0.96774615576744031073999010695171\hspace{0.17em}\mathrm{i}\\ 0.7652087814927846556172932675903+0.83187331431049713218367239317121\hspace{0.17em}\mathrm{i}\\ 0.7652087814927846556172932675903-0.83187331431049713218367239317121\hspace{0.17em}\mathrm{i}\end{array}\right)$$

単純化と操作

Symbolic Math Toolbox は、数学関数の数式処理と単純化をサポートしています。ほとんどの数式は数学的に等価な別の形式で表現でき、Symbolic Math Toolbox では、式の因数分解や展開、項の結合、式の書き換えや並べ替え、仮定に基づいた単純化など、多くの演算をサポートします。

多項式の乗算と結果の単純化を行い、$$(x-1)(x+1)(x^2+x+1)(x^2+1)(x^2-x+1)(x^4-x^2+1)$$ が $$x^{12}-1$$ に単純化されることを示します。

simplify((x - 1)*(x + 1)*(x^2 + x + 1)*(x^2 + 1)*(x^2 - x + 1)*(x^4 - x^2 + 1))

ans = $$x^{12}-1$$

三角恒等式を適用して単純化します (たとえば、$$si{n}^2(x)=\frac{1-cos(2x)}{2}$$ など)。

combine(2*sin(x)*cos(x) + (1- cos(2*x))/2 + cos(x)^2,'sincos')

ans = $$\sin \left(2\hspace{0.17em}x\right)+1$$

多変数多項式を因数分解または展開します。

syms x y
factor(y^6-x^6)

ans = $$\left(\begin{array}{ccccc}-1& x-y& x+y& x^2+x\hspace{0.17em}y+y^2& x^2-x\hspace{0.17em}y+y^2\end{array}\right)$$

f(x) = (x^3 + 7);
expand(f(y-1))

ans = $$y^3-3\hspace{0.17em}{y}^2+3\hspace{0.17em}y+6$$

関数の合成 $$f(g(x))$$ を求めます。

f(x) = sqrt(log(x));
g(x) = sqrt(1-x);
h = compose(g,f,x)

h(x) = $$\sqrt{1-\sqrt{\log \left(x\right)}}$$

微積分 (微分、積分、極限、級数など)

Symbolic Math Toolbox には応用数学向けの微積分ツール一式が揃っています。多変数のシンボリック積分やシンボリック微分を実行できます。級数の生成、操作および計算を行うことができます。

導関数 $$\frac{d}{dx}(\sin (x))$$ を求めます。

diff(sin(x))

ans = $$\cos \left(x\right)$$

連鎖律を使用して、導関数 $$\frac{d}{dx}(x^2+\sin (2x^4)+1)$$ を求めます。

diff(x^2+sin(2*x^4)+1,x)

ans = $$2\hspace{0.17em}x+8\hspace{0.17em}{x}^3\hspace{0.17em}\cos \left(2\hspace{0.17em}{x}^4\right)$$

$$f(x)=e^{\frac{-x^2}{2}}$$ における不定積分 $$\int f(x)dx$$ を求めます。

int(exp(-x^2/2),x)

ans = 
$$\frac{\sqrt{2}\hspace{0.17em}\sqrt{\pi }\hspace{0.17em}\mathrm{erf}\left(\frac{\sqrt{2}\hspace{0.17em}x}{2}\right)}{2}$$

$$f(x)=x\log (1+x)$$ における $$0$$ から $$1$$ までの定積分 $${\int }_a^{b}f(x)dx$$ を求めます。

int(x*log(1+x),0,1)

ans = 
$$\frac{1}{4}$$

$$f(x)=\frac{sin(x)}{x}$$ におけるテイラー級数展開 $$\sum (x-a{)}^n\frac{f^{(n)}(a)}{n!}$$ を $$x=0$$ の点の周辺で計算し、$$x=0$$ において $$\frac{sin(x)}{x}=1$$ であることを示します。

syms x 
T = taylor(sin(x)/x)

T = 
$$\frac{x^4}{120}-\frac{x^2}{6}+1$$

subs(T,x,0)

ans = $$1$$

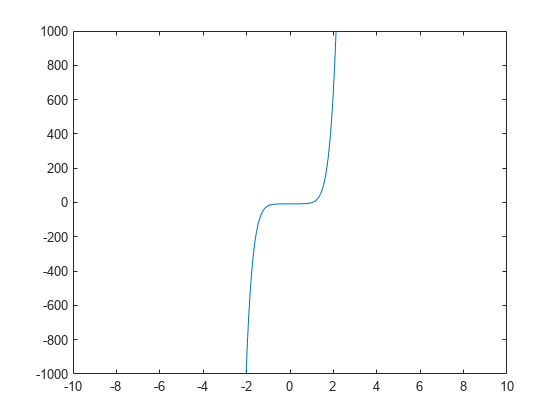
次の左右の極限が等しくないことを示し、$$x=\frac{\pi }{2}$$ において $$tan(x)$$ が不連続であることを示します。$$\underset{x\to {\frac{\pi }{2}}^{+}}{\lim }tan(x)\ne \underset{x\to {\frac{\pi }{2}}^{-}}{\lim }tan(x)$$。

limit(tan(x),x,pi/2,'left')

ans = $$\infty$$

limit(tan(x),x,pi/2,'right')

ans = $$-\infty$$

limit(tan(x),x,pi/2)

ans = $$\mathrm{NaN}$$

微分方程式

Symbolic Math Toolbox は、微分方程式系の求解系を、dsolve を使用して解析的に解くことができます。

1 階 ODE $$\frac{dy}{dx}=-ay$$ を解きます。

syms a b y(x)
dsolve(diff(y) == -a*y)

ans = $$C_1\hspace{0.17em}{\mathrm{e}}^{-a\hspace{0.17em}x}$$

同じ ODE を初期条件 $$y(0)=b$$ を使用して解きます。

dsolve(diff(y)== -a*y,y(0)==b)

ans = $$b\hspace{0.17em}{\mathrm{e}}^{-a\hspace{0.17em}x}$$

連動する 1 階 ODE 系 $$\frac{dx}{dt}=y$$ と $$\frac{dy}{dt}=-x$$ を解きます。

syms x(t) y(t)
z = dsolve(diff(x) == y, diff(y) == -x);
disp([z.x;z.y])

$$\left(\begin{array}{c}{C}_1\hspace{0.17em}\cos \left(t\right)+C_2\hspace{0.17em}\sin \left(t\right)\\ C_2\hspace{0.17em}\cos \left(t\right)-C_1\hspace{0.17em}\sin \left(t\right)\end{array}\right)$$

線形代数

Symbolic Math Toolbox ではシンボリック ベクトルとシンボリック行列を使用できます。シンボリック行列のeigを計算できます。

行列の乗算 $$Ax=b$$ (ここで、$$A=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]$$ および $$x=[x1,x2]$$) を実行します。

syms a b c d
syms x1 x2
x = [x1; x2];
A = [a b ; c d];
b = A*x

b = 
$$\left(\begin{array}{c}a\hspace{0.17em}{x}_1+b\hspace{0.17em}{x}_2\\ c\hspace{0.17em}{x}_1+d\hspace{0.17em}{x}_2\end{array}\right)$$

A の行列式を求めます。

det(A)

ans = $$a\hspace{0.17em}d-b\hspace{0.17em}c$$

A の固有値を求めます。

lambda = eig(A)

lambda = 
$$\left(\begin{array}{c}\frac{a}{2}+\frac{d}{2}-\frac{\sqrt{a^2-2\hspace{0.17em}a\hspace{0.17em}d+d^2+4\hspace{0.17em}b\hspace{0.17em}c}}{2}\\ \frac{a}{2}+\frac{d}{2}+\frac{\sqrt{a^2-2\hspace{0.17em}a\hspace{0.17em}d+d^2+4\hspace{0.17em}b\hspace{0.17em}c}}{2}\end{array}\right)$$

グラフィックス

Symbolic Math Toolbox は 2 次元と 3 次元の解析プロットをサポートします。

fplot(tan(x))

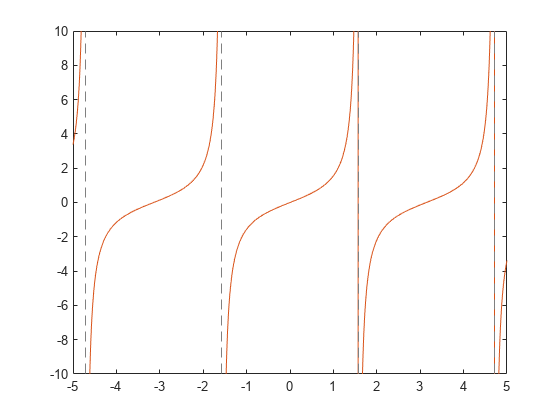
パラメトリック曲線 $$x(t)=t*sin(5t)$$ および $$y(t)=t*cos(5t)$$ をプロットします。

syms t
x = t*sin(5*t); 
y = t*cos(5*t);
fplot(x, y)
grid on

3 次元パラメトリック曲線 $$x(t)=e^{\frac{|t|}{10}}sin(5|t|)$$、$$y(t)=e^{\frac{|t|}{10}}cos(5|t|)$$、および $$z(t)=t$$ の [-10,10] の範囲を赤い破線でプロットします。

syms t
xt = exp(abs(t)/10).*sin(5*abs(t));
yt = exp(abs(t)/10).*cos(5*abs(t));
zt = t;
h = fplot3(xt,yt,zt, [-10,10],'--r');

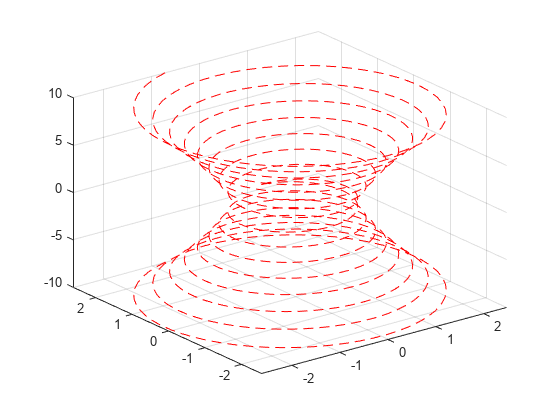
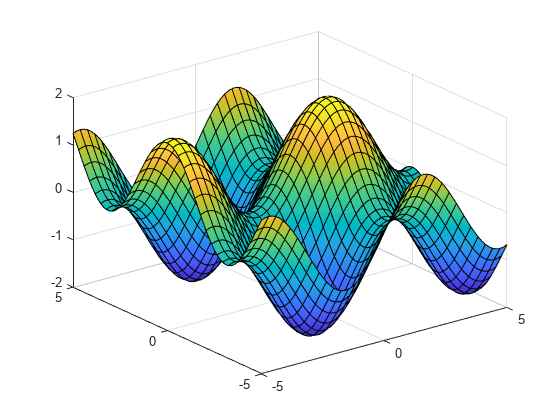
3 次元表面 $$f(x,y)=sin(x)+cos(y)$$ をプロットします。

syms x y
fsurf(sin(x) + cos(y))

同じ表面の 2 次元等高線をプロットします。

fcontour(sin(x) + cos(y))