PCA の使用による米国の都市における生活満足度の分析

この例では、重み付け主成分分析を実行し結果を解釈する方法を示します。

標本データの読み込み

標本データを読み込みます。このデータには、アメリカ合衆国の 329 の都市について、生活の満足度を表す 9 つの異なる指標についての評価点 (気候、住宅、健康、犯罪、交通機関、教育、芸術、娯楽、経済) が含まれています。どのカテゴリでも、高い評価点は満足度の高さを表しています。たとえば、犯罪評価点が高いとは、犯罪率が低いことを意味します。

変数 categories を表示します。

load cities
categories

categories = 9x14 char array
    'climate       '
    'housing       '
    'health        '
    'crime         '
    'transportation'
    'education     '
    'arts          '
    'recreation    '
    'economics     '

cities データ セットには、全部で 3 つの変数があります。

• categories は、指標の名前が含まれている文字行列です。

• names は、329 の都市名が含まれている文字行列です。

• ratings は、329 行 9 列のデータ行列です。

データのプロット

箱ひげ図を作成して、ratings データの分布を確認します。

figure()
boxplot(ratings,'Orientation','horizontal','Labels',categories)

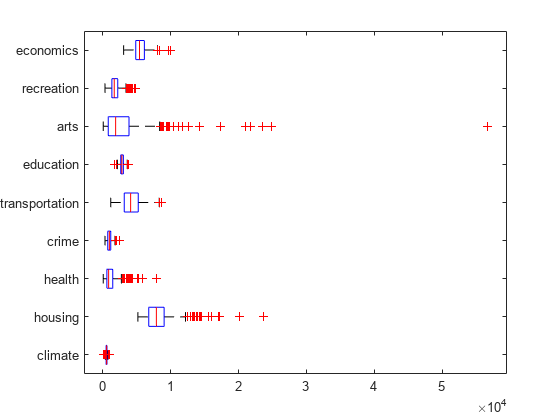
芸術と住宅に関する評価点は、気候や犯罪に関する評価点よりもばらつきが大きくなっています。

ペアワイズ相関の確認

変数間のペアワイズ相関を確認します。

C = corr(ratings,ratings);

一部の変数の相関は 0.85 となっています。主成分分析により、元の変数の線形結合である新しい独立変数が作成されます。

主成分の計算

すべての変数が同じユニットにある場合、生のデータの主成分を計算するのが適切です。変数が異なるユニットにある場合、または異なる列の分散の差が大きい場合 (この例はこれに該当します)、データのスケーリングや重み付けの使用が適していることが多くなります。

評価点の逆分散を重みとして使用し、主成分分析を実行します。

w = 1./var(ratings);
[wcoeff,score,latent,tsquared,explained] = pca(ratings, ...
    'VariableWeights',w);

または、以下を使用することもできます。

[wcoeff,score,latent,tsquared,explained] = pca(ratings, ...
    'VariableWeights','variance');

次の節では、pca の 5 つの出力を説明します。

成分の係数

最初の出力 wcoeff には主成分の係数が含まれています。

初めの 3 つの主成分係数ベクトルは、次のようになります。

c3 = wcoeff(:,1:3)

c3 = 9×3
103 ×

    0.0249   -0.0263   -0.0834
    0.8504   -0.5978   -0.4965
    0.4616    0.3004   -0.0073
    0.1005   -0.1269    0.0661
    0.5096    0.2606    0.2124
    0.0883    0.1551    0.0737
    2.1496    0.9043   -0.1229
    0.2649   -0.3106   -0.0411
    0.1469   -0.5111    0.6586

これらの係数は重み付けされているため、この係数行列は正規直交ではありません。

係数の変換

係数が正規直交するように変換を行います。

coefforth = diag(std(ratings))\wcoeff;

重み付けベクトル w を使用していて、pca を実行する場合は、次のようになります。

coefforth = diag(sqrt(w))*wcoeff;

係数の確認

これで、変換後の係数は正規直交になりました。

I = coefforth'*coefforth;
I(1:3,1:3)

ans = 3×3

    1.0000   -0.0000   -0.0000
   -0.0000    1.0000   -0.0000
   -0.0000   -0.0000    1.0000

成分の得点

2 つ目の出力 score は、主成分によって定義される新しい座標系に元のデータの座標を含んでいます。行列 score は、入力データ行列と同じサイズです。また、正規直交係数と標準化された評価点を次のように使用すると、各成分の得点を求めることができます。

cscores = zscore(ratings)*coefforth;

cscores と score は同じ行列です。

成分の得点のプロット

score の最初の 2 列のプロットを作成します。

figure
plot(score(:,1),score(:,2),'+')
xlabel('1st Principal Component')
ylabel('2nd Principal Component')

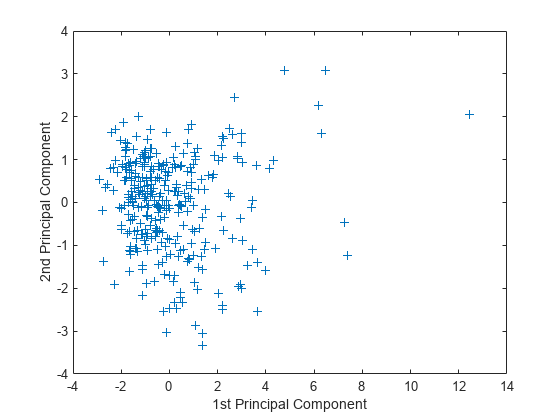
このプロットは、最初の 2 つの主成分に射影された、スケーリングおよびセンタリングされている評価点データを表しています。pca は平均が 0 になるように得点を計算します。

プロットの対話的な表示

プロットの右側の異常点に注意してください。これらの点は次のようにグラフィカルに識別することができます。

gname

カーソルをプロット上に移動させ、右端の 7 つの点の付近で 1 回クリックします。次の図に示すように、点が行番号でラベル付けされます。

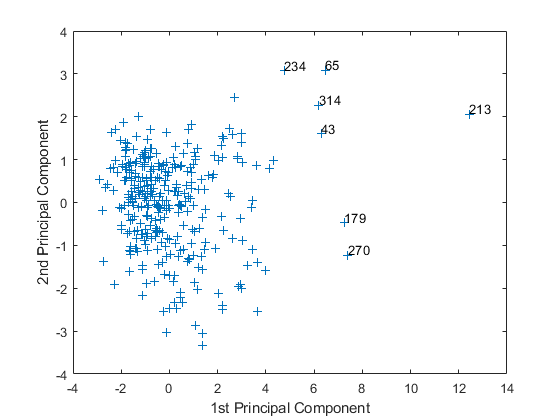
点にラベルが付いたら、"Return" キーを押します。

観測名の抽出

選択したすべての都市の行番号が格納されているインデックス変数を作成し、各都市の名前を取得します。

metro = [43 65 179 213 234 270 314];
names(metro,:)

ans = 7x43 char array
    'Boston, MA                                 '
    'Chicago, IL                                '
    'Los Angeles, Long Beach, CA                '
    'New York, NY                               '
    'Philadelphia, PA-NJ                        '
    'San Francisco, CA                          '
    'Washington, DC-MD-VA                       '

これらのラベル付けされた都市は、米国でも最大の人口密集地の一部であり、他のデータと比べて突出した値になっています。

成分分散

3 つ目の出力 latent は、対応した主成分によって説明された分散を含むベクトルです。score の各列の標本分散は、latent の対応する行と等しくなります。

latent

latent = 9×1

    3.4083
    1.2140
    1.1415
    0.9209
    0.7533
    0.6306
    0.4930
    0.3180
    0.1204

説明されたパーセンテージの分散

5 つ目の出力 explained は、対応する主成分によって説明されたパーセンテージの分散を含むベクトルです。

explained

explained = 9×1

   37.8699
   13.4886
   12.6831
   10.2324
    8.3698
    7.0062
    5.4783
    3.5338
    1.3378

スクリー プロットの作成

各主成分によって説明されるパーセンテージの分散のスクリー プロットを作成します。

figure
pareto(explained)
xlabel('Principal Component')
ylabel('Variance Explained (%)')

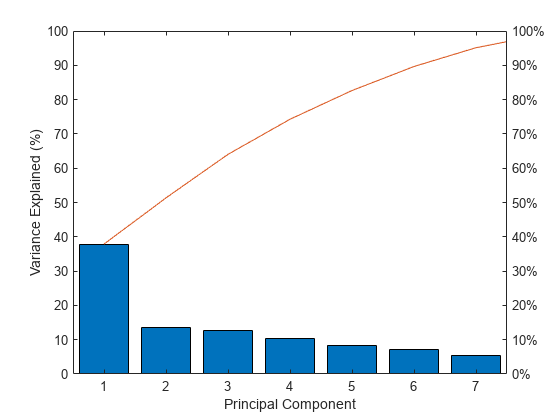
このスクリー プロットには、分散全体の 95% を説明する最初の 7 個の成分のみ (9 個すべてではなく) が表示されます。各成分が占める分散量に明らかな差があるのは、最初と 2 番目の成分のみです。しかし、最初の成分自体は 40% 未満の分散を示すので、より多くの成分が必要になるでしょう。最初の 3 つの主成分は、標準化された評価点の総変動のおよそ 3 分の 2 を説明しているため、次元を削減することは適切な方法と考えられます。

ホテリング T 二乗統計量

pca の最後の出力 tsquared は、ホテリングの T 二乗 ($$T^2$$) であり、データ セットの中心から各観測値までの多変量距離を表す統計的尺度です。これはデータ内の最極の点を見つける分析方法です。

[st2,index] = sort(tsquared,'descend'); % sort in descending order
extreme = index(1);
names(extreme,:)

ans = 
'New York, NY                               '

ニューヨークの評価点は米国全都市の平均から最も離れています。

結果の可視化

各変数の正規直交主成分係数と各観測の主成分得点を 1 つのプロットで可視化します。

figure
biplot(coefforth(:,1:2),'Scores',score(:,1:2),'Varlabels',categories)
axis([-.26 0.6 -.51 .51]);

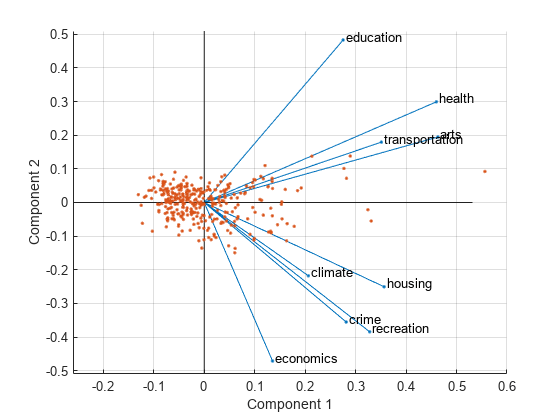
このバイプロットでは、9 つの変数がすべてベクトルで表されます。ベクトルの向きと大きさは、プロットにおける 2 つの主成分に対する各変数の寄与の程度を表します。たとえば、横軸上にある最初の主成分では、9 つの変数すべてに正の係数があります。そのため、9 つのベクトルはプロットの右半分に向いています。第 1 主成分で 1 番大きな係数は、3 番目と 7 番目の要素で、これは変数 health と arts に対応します。

第 2 主成分は縦軸にあり、education、health、arts、transportation の各変数の係数は正で、他の 5 つの変数の係数は負となっています。このことは、第 2 主成分により、変数の最初の組が高い値で 2 番目の組が低い値である都市と、その逆になっている都市が区別されていることを示しています。

この図における変数のラベルは、多少込み合っています。プロットを作成するときに名前と値の引数 VarLabels を除外するか、Figure ウィンドウ ツール バーの [プロット編集] ツールを使用してラベルを選択し適切な位置にドラッグできます。

この 2 次元バイプロットには、329 件の各観測値に対応する点と、プロットの 2 つの主成分に対する各観測値のスコアを示す座標が含まれています。たとえば、このプロットの左端に近い点は、第 1 主成分に対する最小の得点をもちます。各点は得点の最大値と係数の最大長を基準にスケーリングされるため、プロットからは各点の相対位置のみを決定できます。

プロットの項目を指定するには、Figure ウィンドウで [ツール]、[データ ヒント] を選択します。変数 (ベクトル) をクリックすると、各主成分について変数のラベルと係数が表示されます。観測値 (点) をクリックすると、各主成分について観測値の名前とスコアが表示されます。'ObsLabels',names を指定すると、データ カーソル表示で観測値の番号ではなく名前が表示されます。

3 次元バイプロットの作成

また、3 次元のバイプロットを作成することもできます。

figure
biplot(coefforth(:,1:3),'Scores',score(:,1:3),'ObsLabels',names)
axis([-.26 0.8 -.51 .51 -.61 .81])
view([30 40])

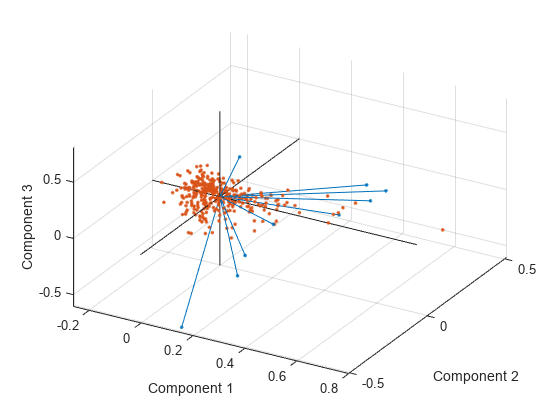
このグラフは、最初の 2 つの主座標がデータの分散を十分に説明しない場合に便利です。また、[ツール]、[3 次元回転] を選択すると、図を回転して別の角度から見ることができます。

参考

pca | pcacov | pcares | ppca | incrementalPCA | boxplot | biplot

関連するトピック

• 主成分分析 (PCA)