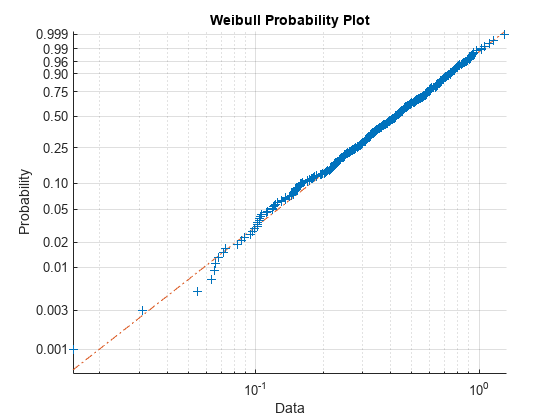
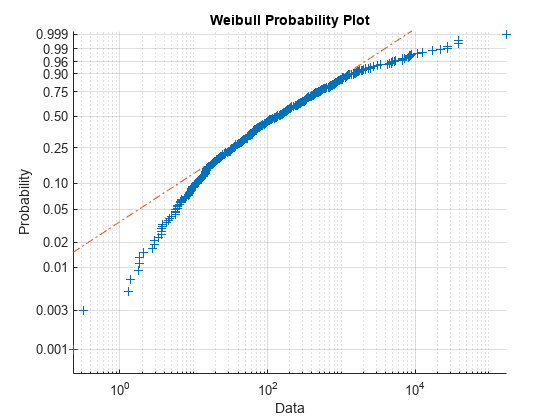
lillietest

リリーフォース検定

構文

h = lillietest(x)

h = lillietest(x,Name,Value)

[h,p] = lillietest(___)

[h,p,kstat,critval] = lillietest(___)

説明

h = lillietest(x) は、リリーフォース検定を使用して、ベクトル x のデータが正規分布族の分布から派生しているという帰無仮説を、正規分布族の分布から派生していないという対立仮説に検定した結果を返します。検定で帰無仮説が有意水準 5% で棄却された場合、結果 h は 1、それ以外の場合は 0 になります。

h = lillietest(x,Name,Value) は、1 つ以上の名前と値の引数ペアで指定された追加オプションを使用して、検定の判定を返します。たとえば、異なる分布族に対してデータを検定したり、有意水準を変更したり、モンテカルロ近似を使用して p 値を計算することができます。

[h,p] = lillietest(___) は、前の構文の入力引数のいずれかを使用して p 値 p も返します。

[h,p,kstat,critval] = lillietest(___) は、検討統計量 kstat および検定の棄却限界値 critval も返します。

例

正規分布の検定

標本データを読み込みます。ガロンあたりの走行マイル数 (MPG) で表した自動車の燃費が、さまざまな車種間で正規分布に従うという帰無仮説を検定します。

load carbig
[h,p,k,c] = lillietest(MPG)

Warning: P is less than the smallest tabulated value, returning 0.001.

h = 
1

p = 
1.0000e-03

k = 
0.0789

c = 
0.0451

検定統計量 k が棄却限界値 c を超えているため、lillietest は、既定の有意水準 5% で帰無仮説を棄却することを示す h = 1 の結果を返します。警告は、事前に計算された値の table に格納されている最小値より小さい $$p$$ 値が返されたことを示しています。より正確な $$p$$ 値を求めるには、MCTol を使用してモンテカルロ近似を実行します。モンテカルロ近似の使用による p 値の決定を参照してください。

さまざまな有意水準で仮説を検定する

標本データを読み込みます。学生の試験の採点データの 1 列目を含むベクトルを作成します。

load examgrades
x = grades(:,1);

標本データは有意水準 1% で標本データが正規分布からのものであるという帰無仮説を検定します。

[h,p] = lillietest(x,'Alpha',0.01)

h = 
0

p = 
0.0348

h = 0 の戻り値は、lillietest が有意水準 1% で帰無仮説を棄却しないことを示します。

指数分布の検定

標本データを読み込みます。ガロンあたりの走行マイル数 (MPG) で表した自動車の燃費が、さまざまな車種間で指数分布に従うという帰無仮説を検定します。

load carbig
h = lillietest(MPG,'Distribution','exponential')

h = 
1

h = 1 の戻り値は、lillietest が既定の有意水準 5% で帰無仮説を棄却することを示します。

ワイブル分布の検定

2 つの標本データ セットを、一方はワイブル分布から、もう一方は対数正規分布から生成します。リリーフォース検定を実行して、各データ セットがワイブル分布からのものかどうかを評価します。ワイブル確率プロット (wblplot) を使用して視覚的に比較することにより、検定の判定を確認します。

ワイブル分布から標本を生成します。

rng('default')
data1 = wblrnd(0.5,2,[500,1]);

lillietest を使用して、リリーフォース検定を実行します。ワイブル分布に対してデータを検定するため、データの対数が極値分布に従うかどうかを検定します。

h1 = lillietest(log(data1),'Distribution','extreme value')

h1 = 
0

h1 = 0 の戻り値は、lillietest が既定の有意水準 5% で帰無仮説を棄却できないことを示します。ワイブル確率プロットを使用して、検定の判定を確認します。

wblplot(data1)

このプロットは、データがワイブル分布に従うことを示しています。

対数正規分布から標本を生成します。

data2 =lognrnd(5,2,[500,1]);

リリーフォース検定を実行します。

h2 = lillietest(log(data2),'Distribution','extreme value')

h2 = 
1

h2 = 1 の戻り値は、lillietest が既定の有意水準 5% で帰無仮説を棄却することを示します。ワイブル確率プロットを使用して、検定の判定を確認します。

wblplot(data2)

このプロットは、データがワイブル分布に従わないことを示しています。

モンテカルロ近似の使用による p 値の決定

標本データを読み込みます。ガロンあたりの走行マイル数 (MPG) で表した自動車の燃費が、さまざまな車種間で正規分布に従うという帰無仮説を検定します。最大モンテカルロ標準誤差が 1e-4 であるモンテカルロ近似を使用して、$$p$$ 値を決定します。

load carbig
[h,p] = lillietest(MPG,'MCTol',1e-4)

h = 
1

p = 
8.3333e-06

h = 1 の戻り値は、lillietest が、有意水準 5% でデータは正規分布から派生するという帰無仮説を棄却することを示します。

入力引数

x — 標本データ

ベクトル

ベクトルとして指定される標本データ。

データ型: single | double

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: 'Distribution','exponential','Alpha',0.01 は、母集団分布は有意水準 1% で指数分布族に属するという帰無仮説を検定します。

Alpha — 有意水準

0.05 (既定値) | (0,1) の範囲のスカラー値

仮説検定の有意水準。'Alpha' と、(0,1) の範囲内のスカラー値で構成されるコンマ区切りのペアとして指定します。

• MCTol が使用されない場合、Alpha は [0.001,0.50] の範囲内でなければなりません。

• MCTol が使用される場合、Alpha は (0,1) の範囲内でなければなりません。

例: 'Alpha',0.01

データ型: single | double

Distribution — 分布族

'normal' (既定値) | 'exponential' | 'extreme value'

仮説検定の分布族。'Distr' と、以下のいずれかで構成されるコンマ区切りペアとして指定します。

'normal'	正規分布
'exponential'	指数分布
'extreme value'	極値分布

• 対数正規分布に対して x を検定するには、log(x) に正規分布があるかどうかを検定します。

• ワイブル分布に対して x を検定するには、log(x) に極値分布があるかどうかを検定します。

例: 'Distribution','exponential'

MCTol — 最大モンテカルロ標準誤差

(0,1) の範囲のスカラー値

検定の p 値 p の最大モンテカルロ標準誤差。'MCTol' と範囲 (0,1) のスカラー値で構成されるコンマ区切りのペアとして指定します。

例: 'MCTol',0.001

データ型: single | double

出力引数

h — 仮説検定の結果

1 | 0

1 または 0 として返される仮説検定の結果。

• 値が 1 の場合、有意水準 Alpha で帰無仮説が棄却されます。

• 値が 0 の場合、有意水準 Alpha では帰無仮説を棄却できません。

p — p 値

(0,1) の範囲のスカラー値

(0,1) の範囲のスカラー値として返される、検定の p 値。p は、帰無仮説に基づく観測値と同様に、極端な検定統計量、またはより極端な検定統計量が観測される確率です。p の値が小さい場合、帰無仮説の妥当性に問題がある可能性があります。

• MCTol が使用されない場合、p は棄却限界値のテーブルへの逆内挿を使用して計算され、範囲 [0.001,0.50] 内のスカラー値として返されます。lillietest は、p が表の範囲内で見つからない場合、表の最小値または最大値を返します。

• MCTol が使用されている場合、lillietest はモンテカルロ シミュレーションを使用して、より正確な p 値を計算し、p は範囲 (0,1) のスカラー値として返されます。

kstat — 検定統計量

非負のスカラー値

検定統計量。非負のスカラー値として返されます。

critval — 棄却限界値

非負のスカラー値

仮説検定の棄却限界値。非負のスカラー値として返されます。

詳細

リリーフォース検定

リリーフォース検定は、帰無分布のパラメーターが未知であるため推定しなければならないという状況に適した両側の適合度検定です。これは、帰無分布が完全に指定されなければならない 1 標本コルモゴロフ・スミルノフ検定とは対照的です。

リリーフォース検定統計量は以下のとおりです。

$$D^{*}=\underset{x}{\max }\left|\widehat{F}\left(x\right)-G\left(x\right)\right|,$$

ここで、$$\widehat{F}\left(x\right)$$ は標本データの経験累積分布関数、$$G\left(x\right)$$ は標本のパラメーターに等しい推定パラメーターをもつ仮定の分布の累積分布関数です。

lillietest を使用すると、データ ベクトルに変換を適用し、適切なリリーフォース検定を実行することで、データ ベクトル x に対数正規分布またはワイブル分布が含まれているかどうかを検定することができます。

• 対数正規分布に対して x を検定するには、log(x) に正規分布があるかどうかを検定します。

• ワイブル分布に対して x を検定するには、log(x) に極値分布があるかどうかを検定します。

リリーフォース検定は、帰無仮説が分布の位置-スケール群でない場合は使用できません。

モンテカルロ標準誤差

モンテカルロ標準誤差は p 値のシミュレーションが原因の誤差です。

モンテカルロ標準誤差は次のように計算されます。

$$SE=\sqrt{\frac{\left(\widehat{p}\right)\left(1-\widehat{p}\right)}{\text{mcreps}}},$$

ここで、$$\widehat{p}$$ は仮説検定について推定した p 値、mcreps は実行したモンテカルロ反復数です。

モンテカルロ反復数 mcreps は、MCTol について指定された値より $$\widehat{p}$$ のモンテカルロ標準誤差が小さくなるように決定されます。

アルゴリズム

仮説検定の棄却限界値を計算するために、lillietest は、標本サイズが 1,000 未満であり、0.001 から 0.50 までの有意水準をもつ標本に対してモンテカルロ シミュレーションを使用し、事前に計算された棄却限界値の表に内挿します。lillietest で使用される表は、リリーフォースによって導入された表よりも大きくて正確です。さらに正確な p 値が必要な場合や、必要な有意水準が 0.001 未満または 0.50 を超える場合、MCTol 入力引数を使用してモンテカルロ シミュレーションを実行し、p 値をさらに正確に計算することができます。

検定統計量の計算された値が棄却限界値よりも大きい場合、lillietest は有意水準 Alpha で帰無仮説を棄却します。

lillietest は、x の NaN 値を欠損値として扱い、無視します。

参照

[1] Conover, W. J. Practical Nonparametric Statistics. Hoboken, NJ: John Wiley & Sons, Inc., 1980.

[2] Lilliefors, H. W. “On the Kolmogorov-Smirnov test for the exponential distribution with mean unknown.” Journal of the American Statistical Association. Vol. 64, 1969, pp. 387–389.

[3] Lilliefors, H. W. “On the Kolmogorov-Smirnov test for normality with mean and variance unknown.” Journal of the American Statistical Association. Vol. 62, 1967, pp. 399–402.

バージョン履歴

R2006a より前に導入

参考

jbtest | kstest | kstest2 | cdfplot | adtest