random

ランダム ノイズがある応答を一般化線形回帰モデルに対するシミュレート

構文

ysim = random(mdl,Xnew)

ysim = random(mdl,Xnew,Name,Value)

説明

ysim = random(mdl,Xnew) は、一般化線形回帰モデル mdl を使用し、ランダム ノイズを追加して、Xnew 内の予測子データに対する応答をシミュレートします。

ysim = random(mdl,Xnew,Name,Value) では、1 つ以上の名前と値のペアの引数を使用して追加オプションを指定します。たとえば、二項分布の試行回数や、当てはめるために使用するオフセット値を指定できます。

例

ランダム ノイズがある応答データのシミュレート

一般化線形回帰モデルを作成し、新しいデータに対するランダム ノイズのある応答をシミュレートします。

基となる 1 つの予測子 X をもつポアソン乱数を使って標本データを生成します。

rng('default') % For reproducibility
X = rand(20,1);
mu = exp(1 + 2*X);
y = poissrnd(mu);

ポアソン データの一般化線形回帰モデルを作成します。

mdl = fitglm(X,y,'y ~ x1','Distribution','poisson');

予測に使用するデータ点を作成します。

Xnew = (0:.05:1)';

データ点でランダム ノイズがある応答をシミュレートします。

ysim = random(mdl,Xnew);

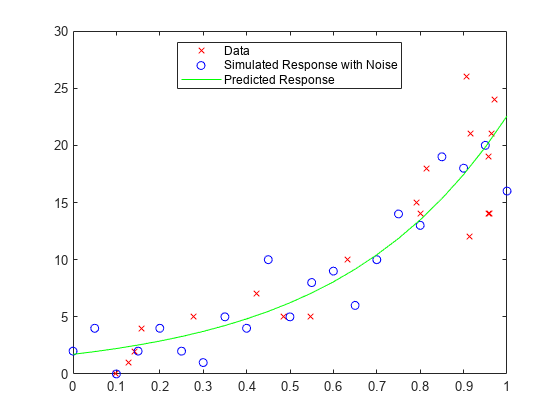
シミュレートされた値と元の値をプロットします。

plot(X,y,'rx',Xnew,ysim,'bo',Xnew,feval(mdl,Xnew),'g-')
legend('Data','Simulated Response with Noise','Predicted Response', ...
    'Location','best')

応答をシミュレートする C/C++ コードの生成

一般化線形回帰モデルを当てはめてから、saveLearnerForCoder を使用してモデルを保存します。loadLearnerForCoderを使用してモデルを読み込み、当てはめたモデルの関数 predict を呼び出す、エントリポイント関数を定義します。その後、codegen (MATLAB Coder) を使用して C/C++ コードを生成します。C/C++ コードの生成には MATLAB® Coder™ が必要であることに注意してください。

この例では、コマンド ラインで線形回帰モデルの予測を行うためのコード生成ワークフローについて簡単に説明します。詳細は、機械学習モデルの予測をコマンド ラインで行うコードの生成を参照してください。MATLAB Coder アプリを使用してコードを生成することもできます。詳細については、機械学習モデルの予測を MATLAB Coder アプリを使用して行うコードの生成を参照してください。

モデルの学習

次の分布で予測子 x および応答 y の標本データを生成します。

• $$x\sim N(1,0.5^2)$$.

• $${\beta }_0=1$$ および $$\beta =-2$$

• $$y\sim Binomial(10,\frac{exp(1+x\beta )}{1+exp(1+x\beta )})$$.

rng('default') % For reproducibility
x = 1 + randn(100,1)*0.5;
beta = -2;
p = exp(1 + x*beta)./(1 + exp(1 + x*beta)); % Inverse logit
n = 10;
y = binornd(n,p,100,1);

二項データの一般化線形回帰モデルを作成します。二項標本サイズとして 10 を指定します。

mdl = fitglm(x,y,'y ~ x1','Distribution','Binomial','BinomialSize',n);

モデルの保存

当てはめた一般化線形回帰モデルを saveLearnerForCoder を使用して GLMMdl.mat というファイルに保存します。

saveLearnerForCoder(mdl,'GLMMdl');

エントリポイント関数の定義

現在のフォルダーで、以下を行う myrandomGLM.m という名前のエントリポイント関数を定義します。

• 新しい予測子入力と、有効な名前と値のペアの引数を受け入れます。

• GLMMdl.mat 内の当てはめた一般化線形回帰モデルを loadLearnerForCoder を使用して読み込みます。

• 読み込んだ GLM モデルから応答をシミュレートします。

function y = myrandomGLM(x,varargin) %#codegen
%MYRANDOMGLM Simulate responses using GLM model 
%   MYRANDOMGLM simulates responses for the n observations in the n-by-1
%   vector x using the GLM model stored in the MAT-file GLMMdl.mat, and
%   then returns the simulations in the n-by-1 vector y.
CompactMdl = loadLearnerForCoder('GLMMdl');
narginchk(1,Inf);
y = random(CompactMdl,x,varargin{:});
end

MATLAB のアルゴリズムについてのコードを生成しようとしていることを指示するため、コンパイラ命令 %#codegen (またはプラグマ) をエントリポイント関数のシグネチャの後に追加します。この命令を追加すると、MATLAB Code Analyzer はコード生成時にエラーになる違反の診断と修正を支援します。

コードの生成

codegen (MATLAB Coder) を使用して、エントリポイント関数のコードを生成します。C および C++ は静的な型の言語なので、エントリポイント関数内のすべての変数のプロパティをコンパイル時に決定しなければなりません。データ型と正確な入力配列のサイズを指定するため、特定のデータ型および配列サイズをもつ一連の値を表す MATLAB® 式を渡します。名前と値のペアの引数の名前に対してcoder.Constant (MATLAB Coder)を使用します。

予測子データ x と二項パラメーター n を指定します。

codegen -config:mex myrandomGLM -args {x,coder.Constant('BinomialSize'),coder.Constant(n)}

Code generation successful.

codegen は、プラットフォームに依存する拡張子をもつ MEX 関数 myrandomGLM_mex を生成します。

コンパイル時に観測値の個数が不明である場合、coder.typeof (MATLAB Coder) を使用して可変サイズの入力を指定することもできます。詳細は、コード生成用の可変サイズ引数の指定 と エントリポイント関数の入力の型の指定 (MATLAB Coder) を参照してください。

生成されたコードの確認

MEX 関数を使用して応答をシミュレートします。予測子データ x と二項パラメーター n を指定します。

ysim = myrandomGLM_mex(x,'BinomialSize',n);

シミュレートした値とデータを同じ Figure にプロットします。

figure
plot(x,y,'bo',x,ysim,'r*')
legend('Observed responses','Simulated responses')
xlabel('x')
ylabel('y')

観測された応答とシミュレートされた応答は、同じ分布になっているように見えます。

入力引数

mdl — 一般化線形回帰モデル

GeneralizedLinearModel オブジェクト | CompactGeneralizedLinearModel オブジェクト

一般化線形回帰モデル。fitglm または stepwiseglm を使用して作成した GeneralizedLinearModel オブジェクト、または compact を使用して作成した CompactGeneralizedLinearModel オブジェクトとして指定します。

Xnew — 新しい予測子の入力値

table | 行列

新しい予測子の入力値。table または行列として指定します。Xnew の各行は 1 つの観測値に対応し、各列は 1 つの変数に対応します。

• Xnew が table である場合、mdl の PredictorNames プロパティの予測子と同じ名前の予測子が含まれていなければなりません。

• Xnew が行列である場合、mdl の作成に使用した予測子入力と同じ個数の変数 (列) が同じ順序で含まれていなければなりません。mdl の作成に使用する変数は、すべて数値でなければなりません。数値予測子をカテゴリカルとして扱うには、mdl を作成するときに名前と値の引数 CategoricalVars を使用して予測子を指定します。

当てはめたモデルで予測子として使用されない予測子変数も Xnew にすべて含めなければならないことに注意してください。

データ型: single | double | table

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: ysim = random(Mdl,Xnew,'BinomialSize',50) は、'BinomialSize' によって指定された試行回数を使用して、ランダム ノイズによる変動があった成功回数を返します。

BinomialSize — 二項分布の試行回数

1 (既定値) | スカラー | ベクトル

二項分布の試行回数。'BinomialSize' と、応答と同じ長さのスカラーまたはベクトルで構成されるコンマ区切りのペアとして指定します。random は、応答と同じサイズの定数配列となるようにスカラー入力を拡張します。スカラー入力は、すべての観測が同じ試行回数であることを意味します。

ysim の出力値の意味は、'BinomialSize' の値によって異なります。

• 'BinomialSize' が 1 (既定) である場合、出力 ysim の各値は成功確率です。

• 'BinomialSize' が 1 でない場合、出力 ysim の各値は試行時の成功予測回数です。

データ型: single | double

Offset — オフセット値

zeros(size(Xnew,1)) (既定値) | スカラー | ベクトル

Xnew の各行のオフセット値。'Offset' と、応答と同じ長さのスカラーまたはベクトルで構成されるコンマ区切りのペアとして指定します。random は、応答と同じサイズの定数配列となるようにスカラー入力を拡張します。

モデルを当てはめるときに名前と値のペアの引数 'Offset' を指定した場合でも、この引数の既定値はゼロのベクトルとなることに注意してください。当てはめるために 'Offset' を指定した場合、ソフトウェアでは 1 で固定した係数値をもつ追加の予測子としてオフセットを扱います。つまり、当てはめのための式は次のようになります

f(μ) = Offset + X*b,

ここで、f はリンク関数、μ は平均応答、X*b は予測子 X の線形結合です。予測子 Offset の係数は 1 です。

データ型: single | double

出力引数

ysim — シミュレートされた応答値

数値ベクトル

シミュレートされた応答値。数値ベクトルとして返されます。シミュレートされた値は、当てはめられたモデルにより与えられた分布をもち、ランダム ノイズによる変動があった Xnew で予測された応答値です。ysim の値は予測子では独立した条件です。二項近似およびポアソン近似の場合、random は推定された分散に対して調整なしで、指定された分布の ysim を生成します。

• 'BinomialSize' が 1 (既定) である場合、出力 ysim の各値は成功確率です。

• 'BinomialSize' が 1 でない場合、出力 ysim の各値は試行時の成功予測回数です。

代替機能

ランダム ノイズのない予測では、predict または feval を使用します。

• predict は、すべての予測子変数を格納する単一の入力引数を受け入れ、予測に対する信頼区間を返します。

• feval は、各予測子変数に 1 つの入力が対応する複数の入力引数を受け入れます。table またはデータセット配列から作成したモデルの場合、この関数をより簡単に使用できます。関数 feval は、名前と値のペアの引数 'Offset' および 'BinomialSize' をサポートしていません。この関数は、オフセット値として 0 を使用し、出力値は予測確率です。

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

• saveLearnerForCoder、loadLearnerForCoder および codegen (MATLAB Coder) を使用して、関数 random のコードを生成します。saveLearnerForCoder を使用して、学習済みモデルを保存します。loadLearnerForCoder を使用して保存済みモデルを読み込んで関数 random を呼び出す、エントリポイント関数を定義します。次に、codegen を使用して、エントリポイント関数のコードを生成します。

• 以下のいずれかに該当する場合、random は MATLAB^® と異なる数列を返す可能性があります。

  • 出力が非スカラーである。

  • 分布に対して入力パラメーターが無効である。

• 次の表は、random の引数に関する注意です。この表に含まれていない引数は、完全にサポートされています。

  引数	注意と制限
  mdl	モデル オブジェクトの使用上の注意および制限については、CompactGeneralizedLinearModel オブジェクトのコード生成を参照してください。
  Xnew	Xnew は、単精度または倍精度の行列か、数値変数、カテゴリカル変数、またはその両方を含む table でなければなりません。 Xnew の行数、または観測値の数は可変サイズにすることができますが、Xnew の列数は固定でなければなりません。 Xnew を table として指定する場合、モデルは table を使用して学習させたものでなければならず、かつ予測のためのエントリポイント関数が次を行うようにしなければなりません。 データを配列として受け入れる データ入力の引数から table を作成し、その table 内で変数名を指定する table を predict に渡す この table のワークフローの例については、table のデータを分類するためのコードの生成を参照してください。コード生成における table の使用の詳細については、table のコード生成 (MATLAB Coder)およびコード生成における table の制限事項 (MATLAB Coder)を参照してください。
  名前と値のペアの引数	名前と値の引数に含まれる名前はコンパイル時の定数でなければなりません。たとえば、生成されたコードで名前と値のペアの引数 'BinomialSize' を使用するには、{coder.Constant('BinomialSize'),0} を codegen (MATLAB Coder) の -args の値に含めます。

詳細は、コード生成の紹介を参照してください。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

この関数は、GPU 配列を完全にサポートします。詳細は、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2012a で導入

参考

GeneralizedLinearModel | CompactGeneralizedLinearModel | predict | feval

トピック

• 新しいデータに対する応答を予測またはシミュレート
• 一般化線形モデル