fscmrmr
Minimum Redundancy Maximum Relevance (MRMR) アルゴリズムを使用した分類用の特徴量のランク付け
構文
説明
fscmrmr は、分類問題用の重要な予測子を識別するために MRMR アルゴリズムを使用して特徴量 (予測子) をランク付けします。
回帰用に MRMR に基づく特徴量のランク付けを実行するには、fsrmrmr を参照してください。
idx = fscmrmr(Tbl,ResponseVarName)idx を返します。table Tbl には予測子変数と応答変数が含まれ、ResponseVarName にクラス ラベルが格納されます。idx を使用して、分類問題用の重要な予測子を選択できます。
idx = fscmrmr(___,Name,Value)
例
標本データを読み込みます。
load ionosphere重要度に基づいて予測子をランク付けします。
[idx,scores] = fscmrmr(X,Y);
予測子の重要度スコアの棒グラフを作成します。
bar(scores(idx)) xlabel('Predictor rank') ylabel('Predictor importance score')
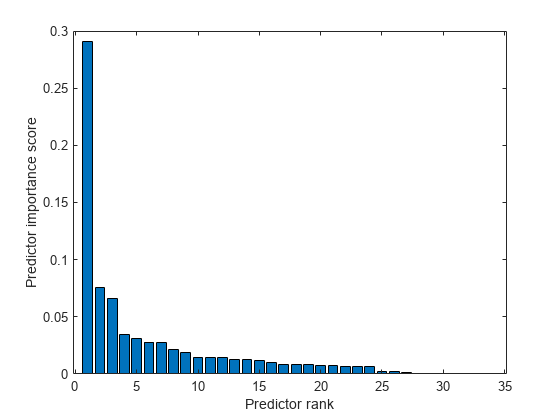
最も重要な予測子の 1 番目と 2 番目の間のスコアの下落は大きいですが、6 番目の予測子の後は比較的小さいです。重要度スコアの下落は、特徴選択の信頼度を表します。したがって、大きな下落は、ソフトウェアが確実に最も重要な予測子を選択していることを示します。小さな下落は、予測子の重要度の差が有意ではないことを示します。
上位 5 つの最も重要な予測子を選択します。X におけるこれらの予測子の列を求めます。
idx(1:5)
ans = 1×5
5 4 1 7 24
X の 5 列目が、Y の最も重要な予測子です。
fscmrmr を使用して重要な予測子を検出します。次に、testckfold を使用して、完全分類モデル (すべての予測子を使用する) と上位 5 つの重要な予測子を使用する次元削減されたモデルの精度を比較します。
census1994 データ セットを読み込みます。
load census1994census1994 内の table adultdata には、個人の年収が $50,000 を超えるかどうかを予測するための、米国勢調査局の人口統計データが含まれています。table の最初の 3 行を表示します。
head(adultdata,3)
age workClass fnlwgt education education_num marital_status occupation relationship race sex capital_gain capital_loss hours_per_week native_country salary
___ ________________ __________ _________ _____________ __________________ _________________ _____________ _____ ____ ____________ ____________ ______________ ______________ ______
39 State-gov 77516 Bachelors 13 Never-married Adm-clerical Not-in-family White Male 2174 0 40 United-States <=50K
50 Self-emp-not-inc 83311 Bachelors 13 Married-civ-spouse Exec-managerial Husband White Male 0 0 13 United-States <=50K
38 Private 2.1565e+05 HS-grad 9 Divorced Handlers-cleaners Not-in-family White Male 0 0 40 United-States <=50K
fscmrmr の出力引数には、関数によってランク付けされた変数のみが含まれます。table を関数に渡す前に、出力引数の順序が table の順序と一致するように、応答変数と重みなどのランク付けを行わない変数をテ table の最後に移動します。
table adultdata では、3 番目の列 fnlwgt はサンプルの重みで、最後の列 salary は応答変数です。関数 movevars を使用して fnlwgt を salary の左側に移動します。
adultdata = movevars(adultdata,'fnlwgt','before','salary'); head(adultdata,3)
age workClass education education_num marital_status occupation relationship race sex capital_gain capital_loss hours_per_week native_country fnlwgt salary
___ ________________ _________ _____________ __________________ _________________ _____________ _____ ____ ____________ ____________ ______________ ______________ __________ ______
39 State-gov Bachelors 13 Never-married Adm-clerical Not-in-family White Male 2174 0 40 United-States 77516 <=50K
50 Self-emp-not-inc Bachelors 13 Married-civ-spouse Exec-managerial Husband White Male 0 0 13 United-States 83311 <=50K
38 Private HS-grad 9 Divorced Handlers-cleaners Not-in-family White Male 0 0 40 United-States 2.1565e+05 <=50K
adultdata の予測子をランク付けします。列 salary を応答変数として指定します。
[idx,scores] = fscmrmr(adultdata,'salary','Weights','fnlwgt');
予測子の重要度スコアの棒グラフを作成します。予測子の名前を x 軸の目盛りラベルに使用します。
bar(scores(idx)) xlabel('Predictor rank') ylabel('Predictor importance score') xticklabels(strrep(adultdata.Properties.VariableNames(idx),'_','\_')) xtickangle(45)
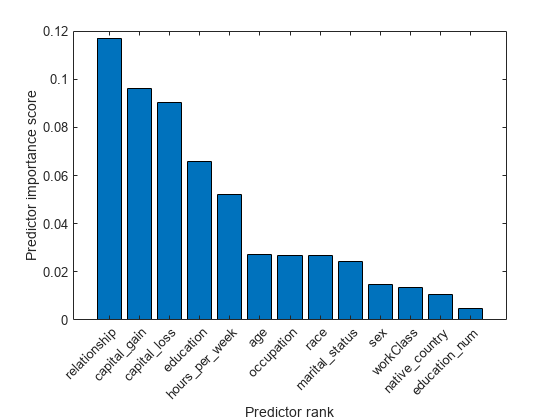
上位 5 つの重要な予測子は、relationship、capital_loss、capital_gain、education および hours_per_week です。
すべての予測子を使用して学習した分類木の精度を、上位 5 つの重要な予測子を使用して学習した分類木の精度と比較します。
既定のオプションを使用して、分類木テンプレートを作成します。
C = templateTree;
すべての予測子を含むように table tbl1 を定義し、上位 5 つの重要な予測子を含むように table tbl2 を定義します。
tbl1 = adultdata(:,adultdata.Properties.VariableNames(idx(1:13))); tbl2 = adultdata(:,adultdata.Properties.VariableNames(idx(1:5)));
分類木テンプレートと 2 つの table を関数testckfoldに渡します。関数は、反復交差検証により 2 つのモデルの精度を比較します。'Alternative','greater' を指定して、すべての予測子を使用するモデルの精度は、5 つの予測子を使用するモデルの精度と同程度であるという帰無仮説を検定します。'Test' が '5x2t' (5 行 2 列のペア t 検定) または '10x10t' (10 行 10 列の反復交差検証 t 検定) である場合、'greater' オプションを使用できます。
[h,p] = testckfold(C,C,tbl1,tbl2,adultdata.salary,'Weights',adultdata.fnlwgt,'Alternative','greater','Test','5x2t')
h = logical
0
p = 0.9970
h が 0 であり、p 値がほぼ 1 であるということは、帰無仮説が棄却できなかったことを示します。5 つの予測子を使用するモデルを使用しても、すべての予測子を使用するモデルと比較して、精度が失われる結果にはなりません。
これで、選択した予測子を使用して分類木を学習させます。
mdl = fitctree(adultdata,'salary ~ relationship + capital_loss + capital_gain + education + hours_per_week', ... 'Weights',adultdata.fnlwgt)
mdl =
ClassificationTree
PredictorNames: {'education' 'relationship' 'capital_gain' 'capital_loss' 'hours_per_week'}
ResponseName: 'salary'
CategoricalPredictors: [1 2]
ClassNames: [<=50K >50K]
ScoreTransform: 'none'
NumObservations: 32561
Properties, Methods
入力引数
標本データ。table として指定します。文字ベクトルの cell 配列ではない cell 配列と複数列の変数は使用できません。
Tbl の各行は 1 つの観測値に、各列は 1 つの予測子変数に対応します。必要に応じて、Tbl に応答変数用および観測値の重み用の追加列を含めることができます。
応答変数は、categorical 配列、文字配列、string 配列、logical ベクトル、数値ベクトル、または文字ベクトルの cell 配列にすることができます。応答変数が文字配列である場合、応答変数の各要素は配列の 1 つの行に対応しなければなりません。
Tblに応答変数が含まれている場合にTbl内の他の変数をすべて予測子として使用するには、ResponseVarNameを使用して応答変数を指定します。Tblに観測値の重みも含まれている場合、Weightsを使用して重みを指定できます。Tblに応答変数が含まれている場合にTbl内の他の変数のサブセットのみを予測子として使用するには、formulaを使用して変数のサブセットを指定します。Tblに応答変数が含まれていない場合は、Yを使用して応答変数を指定します。応答変数とTblの行数は同じでなければなりません。
fscmrmr が Tbl 内の変数のサブセットを予測子として使用する場合、関数はサブセットのみを使用して予測子にインデックスを作成します。名前と値のペアの引数 'CategoricalPredictors' と出力引数 idx 内の値は、関数がランク付けを行わない予測子はカウントしません。
fscmrmr は、応答変数の Tbl に含まれている NaN、'' (空の文字ベクトル)、"" (空の string)、<missing>、および <undefined> の値を欠損値と見なします。fscmrmr は、応答変数に欠損値がある観測値を使用しません。
データ型: table
応答変数名。Tbl 内の変数の名前を含む文字ベクトルまたは string スカラーを指定します。
たとえば、応答変数が Tbl の列 Y (Tbl.Y) である場合、ResponseVarName を "Y" として指定します。
データ型: char | string
応答変数および予測子変数サブセットの説明モデル。"Y ~ x1 + x2 + x3" という形式の文字ベクトルまたは string スカラーとして指定します。この形式では、Y は応答変数を、x1、x2 および x3 は予測子変数を表します。
予測子として Tbl 内の変数のサブセットを指定するには、式を使用します。式を指定した場合、fscmrmr は formula に現れない Tbl 内の変数をランク付けしません。
式の変数名は Tbl の変数名 (Tbl.Properties.VariableNames) であり、有効な MATLAB® 識別子でなければなりません。関数 isvarname を使用して Tbl の変数名を検証できます。変数名が有効でない場合、関数 matlab.lang.makeValidName を使用してそれらを変換できます。
データ型: char | string
応答変数。数値ベクトル、categorical ベクトル、logical ベクトル、文字配列、string 配列、または文字ベクトルの cell 配列として指定します。Y の各行は、X の対応する行のラベルを表します。
fscmrmr は Y に含まれている NaN、'' (空の文字ベクトル)、"" (空の string)、<missing> および <undefined> 値を欠損値と見なします。fscmrmr は、Y に対し欠損値がある観測値を使用しません。
データ型: single | double | categorical | logical | char | string | cell
予測子データ。数値行列として指定します。X の各行は 1 つの観測値に、各列は 1 つの予測子変数に対応します。
データ型: single | double
名前と値の引数
オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。
R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。
例: 'CategoricalPredictors',[1 2],'Verbose',2 は、最初の 2 つの予測子変数をカテゴリカル変数として指定し、詳細レベルを 2 に指定します。
カテゴリカル予測子のリスト。次の表のいずれかの値として指定します。
| 値 | 説明 |
|---|---|
| 正の整数のベクトル | ベクトルの各エントリは、対応する予測子がカテゴリカルであることを示すインデックス値です。インデックス値の範囲は 1 ~
|
| logical ベクトル |
|
| 文字行列 | 行列の各行は予測子変数の名前です。名前は Tbl の名前に一致しなくてはなりません。文字行列の各行が同じ長さになるように、名前を余分な空白で埋めてください。 |
| 文字ベクトルの cell 配列または string 配列 | 配列の各要素は予測子変数の名前です。名前は Tbl の名前に一致しなくてはなりません。 |
"all" | すべての予測子がカテゴリカルです。 |
既定では、予測子データが table (Tbl) の場合、fscmrmr は、その変数が logical ベクトル、順序付けのない categorical ベクトル、文字配列、string 配列、または文字ベクトルの cell 配列のいずれかである場合に、変数を categorical であると見なします。予測子データが行列 (X) である場合、fscmrmr はすべての予測子が連続的であると見なします。他の予測子をカテゴリカル予測子として指定するには、名前と値の引数 CategoricalPredictors を使用してそれらを指定します。
例: "CategoricalPredictors","all"
例: CategoricalPredictors=[1 5 6 8]
データ型: single | double | logical | char | string | cell
ランク付けに使用するクラスの名前。'ClassNames' と categorical 配列、文字配列、string 配列、logical ベクトル、数値ベクトル、または文字ベクトルの cell 配列から構成されるコンマ区切りのペアとして指定します。ClassNames のデータ型は Y または Tbl 内の応答変数と同じでなければなりません。
ClassNames が文字配列の場合、各要素は配列の 1 つの行に対応しなければなりません。
'ClassNames' の使用目的は次のとおりです。
クラスの順序に対応する
Priorの次元の順序を指定する。ランク付け用にクラスのサブセットを選択する。たとえば、
Yに含まれているすべての異なるクラス名の集合が{'a','b','c'}であるとします。クラス'a'および'c'のみの観測値を使用して予測子をランク付けするには、'ClassNames',{'a','c'}を指定します。
'ClassNames' の既定値は、Y または Tbl 内の応答変数に含まれているすべての異なるクラス名の集合です。応答変数に順序がある場合、既定値 'ClassNames' には数学的順序が設定されています。それ以外の場合、既定値にはアルファベット順が設定されています。
例: 'ClassNames',{'b','g'}
データ型: categorical | char | string | logical | single | double | cell
各クラスの事前確率。次のいずれかとして指定します。
文字ベクトルまたは string スカラー。
ベクトル (クラスごとに 1 つのスカラー値)。
'Prior'の対応する要素についてクラスの順序を指定するには、名前と値の引数'ClassNames'を設定します。次の 2 つのフィールドがある構造体
S。S.ClassNamesには、YまたはTblの応答変数と同じ型の変数のクラス名が格納されます。S.ClassProbsには、対応する確率のベクトルが格納されます。
fscmrmr は、合計がクラスの事前確率の値になるように各クラスの重み ('Weights') を正規化します。
例: 'Prior','uniform'
データ型: char | string | single | double | struct
予測子内の欠損値を使用するかどうかを示すインジケーター。ランク付けに値を使用する場合は true、値を破棄する場合は false として指定します。
fscmrmr は、NaN、'' (空の文字ベクトル)、"" (空の string)、<missing>、および <undefined> の値を欠損値と見なします。
UseMissing を true として指定した場合、fscmrmr はランク付けに欠損値を使用します。カテゴリカル変数の場合、fscmrmr は欠損値を追加のカテゴリとして扱います。連続変数の場合、fscmrmr はビン化するために別個のビン内に NaN 値を配置します。
UseMissing を false として指定した場合、fscmrmr はランク付けに欠損値を使用しません。fscmrmr は変数の各ペアについて相互情報を計算するため、関数は行内の値が部分的に欠損している場合も行全体を破棄することはありません。fscmrmr は、欠損値を含まないすべてのペアの値を使用します。
例: "UseMissing",true
例: UseMissing=true
データ型: logical
詳細レベル。'Verbose' と非負の整数値から構成されるコンマ区切りのペアとして指定します。Verbose の値は、コマンド ウィンドウに表示される診断情報の量を制御します。
0 —
fscmrmrは診断情報を何も表示しません。1 —
fscmrmrは、相互情報の計算と予測子のランク付けにかかる経過時間を表示します。≥ 2 —
fscmrmrは、経過時間と相互情報の計算に関連する追加メッセージを表示します。情報の量は、'Verbose'値が増加するにつれて増加します。
例: 'Verbose',1
データ型: single | double
観測値の重み。'Weights' とスカラー値のベクトルまたは Tbl 内の変数の名前から構成されるコンマ区切りのペアとして指定します。関数は、X または Tbl の各行の観測値に、Weights の対応する値で重みを付けます。Weights のサイズは、X または Tbl の行数と同じでなければなりません。
入力データを table Tbl として指定した場合、Weights は数値ベクトルが含まれている Tbl 内の変数の名前にすることができます。この場合、Weights には文字ベクトルまたは string スカラーを指定しなければなりません。たとえば、重みベクトルが Tbl の列 W (Tbl.W) である場合、'Weights,'W' を指定します。
fscmrmr は、合計がクラスの事前確率の値になるように各クラスの重みを正規化します。Inf の重みはサポートされません。
データ型: single | double | char | string
出力引数
予測子の重要度順に並べ替えられた X または Tbl の予測子のインデックス。1 行 r 列の数値ベクトルとして返されます。r はランク付けされた予測子の数です。
Tbl に応答変数が含まれている場合、関数は応答変数を除外して予測子にインデックスを付けます。たとえば、Tbl に列が 10 個あり、Tbl の 2 列目を応答変数として指定するとします。idx(3) が 5 である場合、3 番目に重要な予測子は Tbl の 6 列目です。
fscmrmr が Tbl 内の変数のサブセットを予測子として使用する場合、関数はサブセットのみを使用して予測子にインデックスを作成します。たとえば、Tbl に列が 10 個あり、formula を使用して Tbl の最後の 5 列を予測子変数として指定するとします。idx(3) が 5 である場合、3 番目に重要な予測子は Tbl の 10 列目 (サブセットの 5 番目の予測子) です。
予測子スコア。1 行 r 列の数値ベクトルとして返されます。r はランク付けされた予測子の数です。
大きなスコア値は、対応する予測子が重要であることを示します。また、特徴量の重要度スコアの下落は、特徴選択の信頼度を表します。たとえば、ソフトウェアが確実に特徴量 x を選択している場合、次に最も重要な特徴量のスコア値が x のスコア値よりさらに小さくなります。
たとえば、Tbl に列が 10 個あり、formula を使用して Tbl の最後の 5 列を予測子変数として指定するとします。この場合、score(3) には Tbl 内の 8 番目の列のスコア値が含まれます。これは、サブセットの 3 番目の予測子です。
詳細
2 つの変数間の相互情報は、ある変数の不確かさの度合いが、他の変数がわかるとどの程度削減できるかを測定します。
離散確率変数 X と Z の相互情報 I は、
として定義されます。X と Z が独立している場合、I は 0 と等しくなります。X と Z が同じ確率変数である場合、I は X のエントロピーと等しくなります。
関数 fscmrmr は、この定義を使用して、カテゴリカル (離散) 変数および連続変数の両方の相互情報の値を計算します。fscmrmr は、連続変数を 256 個のビンか、それが 256 個より少ない場合は変数内の独自の値の数に離散化させます。関数は、適応アルゴリズムを使用して変数の各ペアに最適な二変量ビンを求めます [2]。
アルゴリズム
MRMR アルゴリズム[1]は、相互に、最大に類似していない最適な特徴量のセットを求め、応答変数を効率的に表すことができます。このアルゴリズムにより、特徴セットの冗長性が最小化され、応答変数に対する特徴量セットの関連性が最大化されます。変数の相互情報を使用して、冗長性と関連性、つまり特徴量のペアワイズ相互情報と特徴量および応答の相互情報が定量化されます。このアルゴリズムを分類問題に使用できます。
MRMR アルゴリズムの目的は、応答変数 y に関して VS (S の関連性) を最大化し、WS (S の冗長性) を最小化する特徴量の最適なセット S を検出することです。ここで、VS と WS は相互情報 I を使用して定義されます。
|S| は S 内の特徴量の数です。
最適なセット S の検出には、すべての 2|Ω| の組み合わせを考慮することが必要です。ここで、Ω は特徴セット全体です。代わりに、MRMR アルゴリズムは前方追加方式により特徴量をランク付けします。これには、Mutual Information Quotient (MIQ) の値を使用した O(|Ω|·|S|) 計算が必要です。
ここで Vx と Wx は、それぞれ特徴量の関連性と冗長性です。
関数 fscmrmr は MRMR アルゴリズムを使用して Ω 内のすべての特徴量をランク付けし、idx (特徴量の重要度順に並べ替えられた特徴量のインデックス) を返します。したがって、計算コストは O(|Ω|2) となります。関数は、ヒューリスティックなアルゴリズムを使用して特徴量の重要度を定量化し、スコア (scores) を返します。大きなスコア値は、対応する予測子が重要であることを示します。また、特徴量の重要度スコアの下落は、特徴選択の信頼度を表します。たとえば、ソフトウェアが確実に特徴量 x を選択している場合、次に最も重要な特徴量のスコア値が x のスコア値よりさらに小さくなります。出力を使用して、特徴量の特定の数の最適なセット S を検出します。
fscmrmr は次のように特徴量をランク付けします。
関連性が最も高い特徴量 を選択します。選択した特徴量を空のセット S に追加します。
S、Sc の補数の関連性が非ゼロで冗長性がゼロである特徴量を検出します。
関連性が非ゼロで冗長性がゼロである特徴量が Sc に含まれていない場合、ステップ 4 に進みます。
それ以外の場合、関連性が最も高い特徴量 を選択します。選択した特徴量をセット S に追加します。
Sc のすべての特徴量について冗長性がゼロではなくなるまでステップ 2 を繰り返します。
Sc の関連性が非ゼロで冗長性が非ゼロの、MIQ の最大値をもつ特徴量を選択し、選択した特徴量をセット S に追加します。
Sc のすべての特徴量について関連性がゼロになるまでステップ 4 を繰り返します。
関連性がゼロである特徴量を無作為順で S に追加します。
ソフトウェアでステップ内に記述されている条件を満たす特徴量を検出できない場合、任意のステップを省略できます。
参照
[1] Ding, C., and H. Peng. "Minimum redundancy feature selection from microarray gene expression data." Journal of Bioinformatics and Computational Biology. Vol. 3, Number 2, 2005, pp. 185–205.
[2] Darbellay, G. A., and I. Vajda. "Estimation of the information by an adaptive partitioning of the observation space." IEEE Transactions on Information Theory. Vol. 45, Number 4, 1999, pp. 1315–1321.
バージョン履歴
R2019b で導入R2020a 以降は、'UseMissing' の名前と値のペアの引数を使用することによって、ランク付けに予測子内の欠損値を使用するか破棄するかを指定できます。'UseMissing' の既定値は false です。これは、Statistics and Machine Learning Toolbox™ のほとんどの分類学習関数が学習に欠損値を使用しないためです。
R2019b では、fscmrmr が既定で予測子内の欠損値を使用していました。コードを更新するには、'UseMissing',true を指定します。
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)