GapEvaluation
ギャップ基準クラスタリング評価オブジェクト
説明
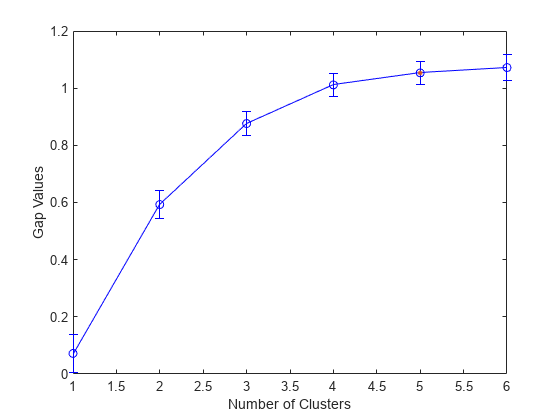
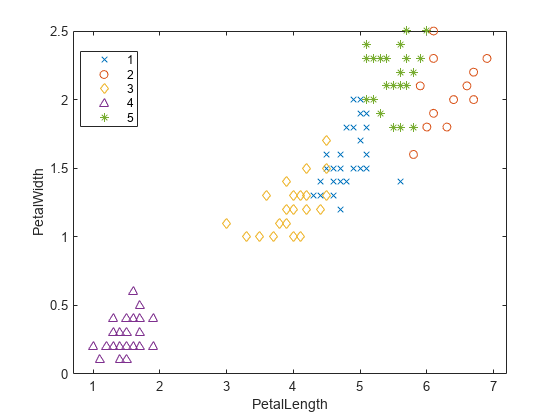
GapEvaluation は、標本データ (X)、クラスタリング データ (OptimalY) およびギャップ基準値 (CriterionValues) で構成されるオブジェクトであり、最適なクラスター数 (OptimalK) を評価するために使用されます。ギャップ基準値は差分 ExpectedLogW – LogW に対応します。ここで、W はクラスター内の分散で、ExpectedLogW は参照分布からのモンテカルロ サンプリングによって決定され、LogW は標本データから計算されます。最適なクラスター数は、許容誤差の範囲内でローカルまたはグローバルなギャップ値が最大になる解に対応します (SearchMethod)。詳細は、ギャップ値を参照してください。
作成
ギャップ基準クラスタリング評価オブジェクトを作成するには、関数 evalclusters を使用し、基準を "gap" と指定します。
その後、compact を使用して、コンパクトなバージョンのギャップ基準クラスタリング評価オブジェクトを作成できます。この関数は、プロパティ X、OptimalY、および Missing の内容を削除します。
プロパティ
オブジェクト関数
例
ギャップ クラスタリング評価基準を使用して最適なクラスター数を評価します。
fisheriris データ セットを読み込みます。このデータには、3 種のアヤメの花のがく片と花弁からの長さと幅の測定値が含まれています。
load fisheririsギャップ基準値に基づいて最適なクラスター数を評価します。データのクラスタリングには kmeans を使用します。
rng("default") % For reproducibility evaluation = evalclusters(meas,"kmeans","gap","KList",1:6)
evaluation =
GapEvaluation with properties:
NumObservations: 150
InspectedK: [1 2 3 4 5 6]
CriterionValues: [0.0720 0.5928 0.8762 1.0114 1.0534 1.0720]
OptimalK: 5
Properties, Methods
OptimalK の値は、ギャップ基準に基づく最適なクラスター数が 5 であることを示しています。
テストした各クラスター数について、ギャップ基準値をプロットします。
plot(evaluation)
このプロットでは、クラスター数が 6 の場合にギャップ基準の値が最大になっています。しかし、クラスター数 5 に対する値は最大から 1 標準偏差以内にあるので、推奨される最適なクラスター数は 5 です。
グループ化した散布図を作成して花弁の長さと幅の関係を調べます。データは推奨されるクラスターごとにグループ化します。
PetalLength = meas(:,3);
PetalWidth = meas(:,4);
clusters = evaluation.OptimalY;
gscatter(PetalLength,PetalWidth,clusters,[],"xod^*");
このプロットは、左下のクラスター 4 が他の 4 つのクラスターから完全に分離されていることを示しています。クラスター 4 には花弁の幅と長さが最も小さい花が含まれています。クラスター 2 は右上にあり、花弁の幅と長さが最も大きい花が含まれています。クラスター 5 はクラスター 2 の横にあり、クラスター 2 の花と比較して花弁の幅は同様であるが長さは短い花が含まれています。クラスター 1 および 3 はプロットの中央付近にあり、測定値が極端な値ではない花が含まれています。
詳細
参照
[1] Tibshirani, R., G. Walther, and T. Hastie. “Estimating the number of clusters in a data set via the gap statistic.” Journal of the Royal Statistical Society: Series B. Vol. 63, Part 2, 2001, pp. 411–423.
バージョン履歴
R2013b で導入
