ハード クラスタリングの使用による混合ガウス データのクラスタリング

この例では、ガウス分布の混合からシミュレートされたデータに対するハード クラスタリングの実装方法を示します。

近似させたモデルの多変量正規成分でクラスターを表すことができるので、混合ガウス モデルをデータのクラスタリングに使用できます。

ガウス分布の混合から派生するデータのシミュレート

mvnrndを使用して、2 つの二変量ガウス分布の混合から派生するデータをシミュレートします。

rng('default')  % For reproducibility
mu1 = [1 2];
sigma1 = [3 .2; .2 2];
mu2 = [-1 -2];
sigma2 = [2 0; 0 1];
X = [mvnrnd(mu1,sigma1,200); mvnrnd(mu2,sigma2,100)];
n = size(X,1);

figure
scatter(X(:,1),X(:,2),10,'ko')

シミュレーション データへの混合ガウス モデルの当てはめ

2 成分の混合ガウス モデル (GMM) を当てはめます。ここでは正しい成分数がわかっていますが、実際に、本物のデータを使用する場合は、さまざまな成分数をもつモデルを比較して決定する必要があります。また、期待値最大化近似ルーチンの最終反復の表示を要求します。

options = statset('Display','final'); 
gm = fitgmdist(X,2,'Options',options)

26 iterations, log-likelihood = -1210.59

gm = 

Gaussian mixture distribution with 2 components in 2 dimensions
Component 1:
Mixing proportion: 0.629514
Mean:    1.0756    2.0421

Component 2:
Mixing proportion: 0.370486
Mean:   -0.8296   -1.8488

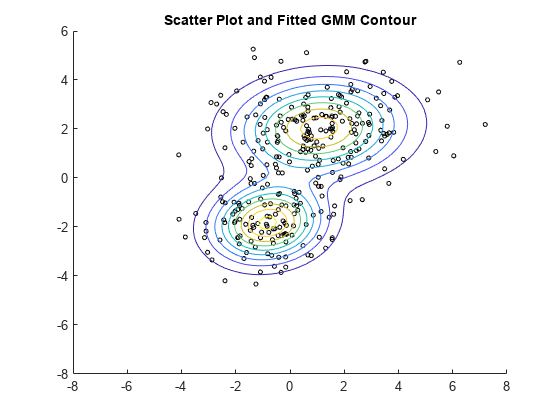
2 成分混合分布の推定確率密度等高線をプロットします。2 つの二変量正規分布成分は部分的に重なりますが、ピークは異なっています。これにより、データを 2 つのクラスターに適切に分割できることがわかります。

hold on
gmPDF = @(x,y) arrayfun(@(x0,y0) pdf(gm,[x0,y0]),x,y);
fcontour(gmPDF,[-8,6])
title('Scatter Plot and Fitted GMM Contour')
hold off

近似させた GMM の使用によるデータのクラスタリング

clusterは、各データ点を正確に 1 つのクラスターに割り当てるメソッド、"ハード クラスタリング" を実装します。GMM の場合、cluster は GMM に含まれている 2 つの混合成分のいずれかに各点を割り当てます。各クラスターの中心は、対応する混合成分の平均です。"ソフト クラスタリング" についての詳細は、ソフト クラスタリングの使用による混合ガウス データのクラスタリングを参照してください。

近似させた GMM とデータを cluster に渡すことにより、データをクラスターに分割します。

idx = cluster(gm,X);
cluster1 = (idx == 1); % |1| for cluster 1 membership
cluster2 = (idx == 2); % |2| for cluster 2 membership

figure
gscatter(X(:,1),X(:,2),idx,'rb','+o')
legend('Cluster 1','Cluster 2','Location','best')

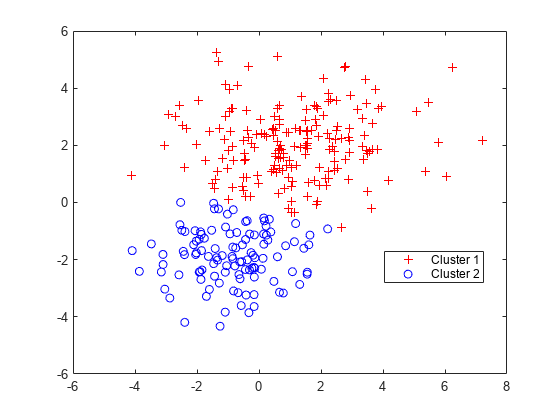
各クラスターは、混合分布に含まれている二変量正規成分のいずれかに対応します。cluster は、クラスター メンバーシップ スコアに基づいてデータをクラスターに割り当てます。各クラスター メンバーシップ スコアとは、対応する成分からそのデータ点が派生する事後確率の推定値です。cluster は、各点の最大の事後確率に対応する混合成分にその点を割り当てます。

クラスター メンバーシップの事後確率は、近似させた GMM とデータを次のいずれかに渡すことにより推定できます。

• posterior

• cluster (3 番目の出力引数を返すように要求)

クラスター メンバーシップの事後確率の推定

各点について 1 番目の成分の事後確率を推定およびプロットします。

P = posterior(gm,X); 

figure
scatter(X(cluster1,1),X(cluster1,2),10,P(cluster1,1),'+')
hold on
scatter(X(cluster2,1),X(cluster2,2),10,P(cluster2,1),'o')
hold off
clrmap = jet(80);
colormap(clrmap(9:72,:))
ylabel(colorbar,'Component 1 Posterior Probability')
legend('Cluster 1','Cluster 2','Location','best')
title('Scatter Plot and Cluster 1 Posterior Probabilities')

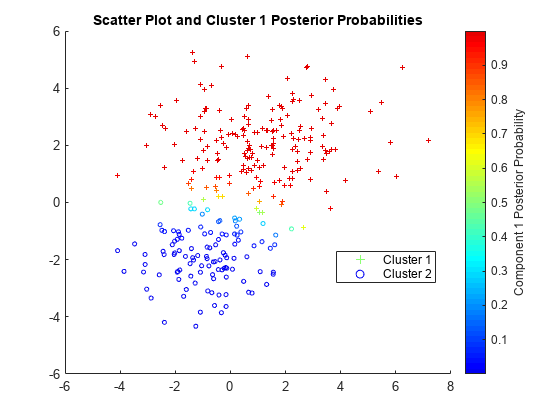
P は、クラスター メンバーシップの事後確率が含まれている n 行 2 列の行列です。1 番目の列にはクラスター 1 の事後確率が含まれており、2 番目の列はクラスター 2 の事後確率に対応します。

新しいデータのクラスターへの代入

cluster メソッドを使用して、元のデータから求めた混合成分に新しいデータ点を割り当てることもできます。

ガウス分布の混合から派生する新しいデータをシミュレートします。mvnrnd を使用するのではなく、gmdistributionを使用して真の混合成分の平均と標準偏差で GMM を作成してから GMM をrandomに渡すことにより、データをシミュレートできます。

Mu = [mu1; mu2]; 
Sigma = cat(3,sigma1,sigma2); 
p = [0.75 0.25]; % Mixing proportions

gmTrue = gmdistribution(Mu,Sigma,p);
X0 = random(gmTrue,75);

近似させた GMM (gm) と新しいデータを cluster に渡すことにより、新しいデータにクラスターを割り当てます。クラスター メンバーシップの事後確率を要求します。

[idx0,~,P0] = cluster(gm,X0);

figure
fcontour(gmPDF,[min(X0(:,1)) max(X0(:,1)) min(X0(:,2)) max(X0(:,2))])
hold on
gscatter(X0(:,1),X0(:,2),idx0,'rb','+o')
legend('Fitted GMM Contour','Cluster 1','Cluster 2','Location','best')
title('New Data Cluster Assignments')
hold off

新しいデータをクラスタリングするときに意味がある結果を cluster に生成させるには、混合分布を作成するために使用した元のデータである X と同じ母集団から X0 が派生する必要があります。特に、X0 の事後確率を計算するときに、cluster と posterior は混合確率の推定値を使用します。

参考

fitgmdist | gmdistribution | cluster | posterior | random

関連するトピック

• 混合ガウス モデルを使用したクラスタリング
• ソフト クラスタリングの使用による混合ガウス データのクラスタリング
• 混合ガウス モデルの調整
• クラスター分析手法の選択