ソフト クラスタリングの使用による混合ガウス データのクラスタリング

この例では、ガウス分布の混合からシミュレートされたデータに対するソフト クラスタリングの実装方法を示します。

clusterは、クラスター メンバーシップの事後確率を推定してから、最大の事後確率に対応するクラスターに各点を割り当てます。ソフト クラスタリングは、データ点が複数のクラスターに属することができる、別のクラスタリング手法です。ソフト クラスタリングを実装するには、次のようにします。

1. 各点が各クラスターの原型にどのくらい似ているかを示すクラスタリング メンバーシップ スコアを各データ点に割り当てます。ガウス分布の混合の場合、クラスターの原型は対応する成分の平均であり、この成分は推定したクラスター メンバーシップの事後確率になることができます。

2. クラスター メンバーシップ スコアによって点にランクを付けます。

3. スコアを調べ、クラスター メンバーシップを決定します。

事後確率をスコアとして使用するアルゴリズムの場合、データ点は最大の事後確率に対応するクラスターのメンバーになります。しかし、対応する事後確率が最大値に近い他のクラスターがある場合、データ点はそのクラスターのメンバーになることもできます。クラスタリングの前に、複数のクラスター メンバーシップを得るようにスコアのしきい値を決定することをお勧めします。

この例は、ハード クラスタリングの使用による混合ガウス データのクラスタリングの続きです。

2 つの二変量ガウス分布の混合から派生するデータをシミュレートします。

rng(0,'twister')  % For reproducibility
mu1 = [1 2];
sigma1 = [3 .2; .2 2];
mu2 = [-1 -2];
sigma2 = [2 0; 0 1];
X = [mvnrnd(mu1,sigma1,200); mvnrnd(mu2,sigma2,100)];

2 成分の混合ガウス モデル (GMM) を当てはめます。2 つの成分があるので、クラスター メンバーシップの事後確率が [0.4,0.6] の区間にあるすべてのデータ点は、両方のクラスターのメンバーになることが可能と仮定します。

gm = fitgmdist(X,2);
threshold = [0.4 0.6];

近似させた GMM gm を使用して、すべてのデータ点について成分メンバーの事後確率を推定します。これらは、クラスター メンバーシップ スコアを表します。

P = posterior(gm,X);

各クラスターについて、すべてのデータ点のメンバーシップ スコアをランク付けします。各クラスターについて、他のすべてのデータ点に対するランキングに関してデータ点のメンバーシップ スコアをプロットします。

n = size(X,1);
[~,order] = sort(P(:,1));

figure
plot(1:n,P(order,1),'r-',1:n,P(order,2),'b-')
legend({'Cluster 1', 'Cluster 2'})
ylabel('Cluster Membership Score')
xlabel('Point Ranking')
title('GMM with Full Unshared Covariances')

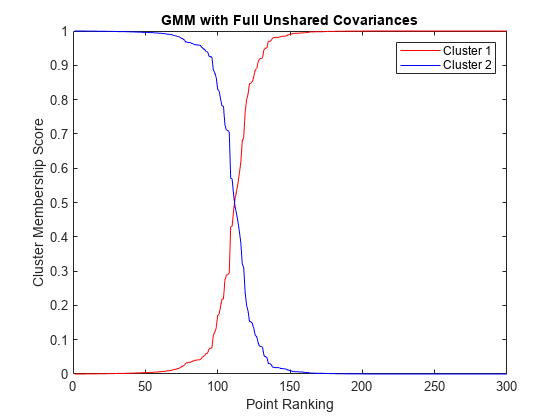
データの散布図で明確な分離を確認するのは困難ですが、メンバーシップ スコアをプロットすると、近似させた分布では適切にデータをグループに分離できていることがわかります。

データをプロットし、最大事後確率別にクラスターを割り当てます。いずれかのクラスターに属することができる点を識別します。

idx = cluster(gm,X);
idxBoth = find(P(:,1)>=threshold(1) & P(:,1)<=threshold(2)); 
numInBoth = numel(idxBoth)

numInBoth = 7

figure
gscatter(X(:,1),X(:,2),idx,'rb','+o',5)
hold on
plot(X(idxBoth,1),X(idxBoth,2),'ko','MarkerSize',10)
legend({'Cluster 1','Cluster 2','Both Clusters'},'Location','SouthEast')
title('Scatter Plot - GMM with Full Unshared Covariances')
hold off

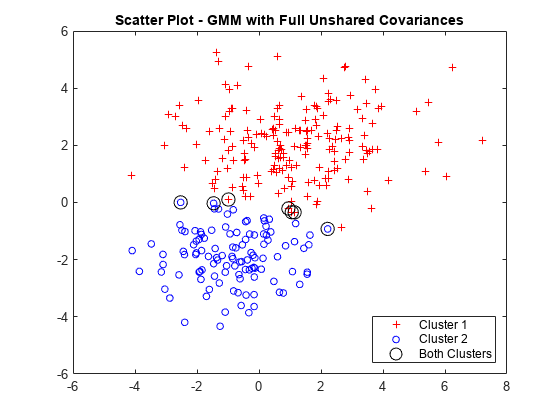
スコアのしきい値区間を使用すると、7 つのデータ点はいずれかのクラスターに属することができます。

GMM を使用するソフト クラスタリングでは、ファジィ k-means クラスタリングと同じように、メンバーシップ スコアを使用して各点を各クラスターに割り当てます。ファジィ k-means アルゴリズムでは、クラスターの形状が球面に近く、どのクラスターもほぼ同じサイズであると仮定します。これは、すべての成分間で共有され、単位行列の倍数である 1 つの共分散行列をもつ混合ガウス分布に相当します。対照的に、gmdistribution ではさまざまな共分散の構造を指定できます。既定の設定のオプションでは、成分ごとに制約のない共分散行列を推定します。k-means に近い、より制限されたオプションとして、共有した対角共分散行列を推定するというものがあります。

GMM をデータに当てはめますが、同じ対角共分散行列を各成分が共有するように指定します。このように指定するとファジィ k-means クラスタリングを実行する場合と同じようになりますが、変数ごとに異なる分散が可能なので、柔軟性が高くなります。

gmSharedDiag = fitgmdist(X,2,'CovType','Diagonal', ...
    'SharedCovariance',true');

近似させた GMM gmSharedDiag を使用して、すべてのデータ点について成分メンバーの事後確率を推定します。ソフト クラスターの割り当てを推定します。

[idxSharedDiag,~,PSharedDiag] = cluster(gmSharedDiag,X);
idxBothSharedDiag = find(PSharedDiag(:,1)>=threshold(1) & ...
    PSharedDiag(:,1)<=threshold(2)); 
numInBoth = numel(idxBothSharedDiag)

numInBoth = 5

成分間で対角共分散を共有すると、5 つのデータ点がいずれかのクラスターに属することができます。

各クラスターについて、次のようにします。

1. すべてのデータ点についてメンバーシップ スコアをランク付けします。

2. 他のすべてのデータ点に対するランキングに関して、各データ点のメンバーシップ スコアをプロットします。

[~,orderSharedDiag] = sort(PSharedDiag(:,1));

figure
plot(1:n,PSharedDiag(orderSharedDiag,1),'r-',...
    1:n,PSharedDiag(orderSharedDiag,2),'b-')
legend({'Cluster 1' 'Cluster 2'},'Location','NorthEast')
ylabel('Cluster Membership Score')
xlabel('Point Ranking')
title('GMM with Shared Diagonal Component Covariances')

データをプロットし、成分間で対角共分散が共有されると仮定した GMM 分析からハードなクラスタリング割り当てを識別します。また、いずれかのクラスターに属することができるデータ点を識別します。

figure
gscatter(X(:,1),X(:,2),idxSharedDiag,'rb','+o',5)
hold on
plot(X(idxBothSharedDiag,1),X(idxBothSharedDiag,2),'ko','MarkerSize',10)
legend({'Cluster 1','Cluster 2','Both Clusters'},'Location','SouthEast')
title('Scatter Plot - GMM with Shared Diagonal Component Covariances')
hold off

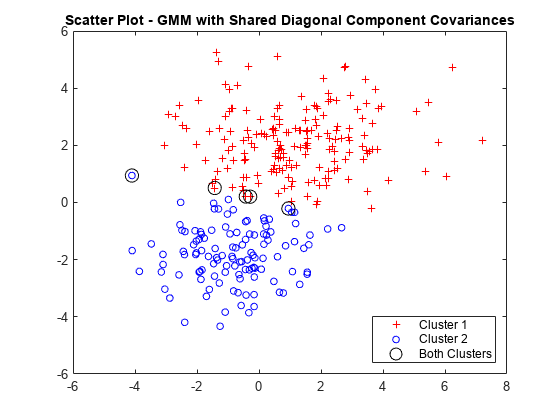
参考

fitgmdist | gmdistribution | cluster

関連するトピック

• 混合ガウス モデルを使用したクラスタリング
• ハード クラスタリングの使用による混合ガウス データのクラスタリング
• 混合ガウス モデルの調整
• クラスター分析手法の選択