bootci

ブートストラップ信頼区間

構文

ci = bootci(nboot,bootfun,d)

ci = bootci(nboot,bootfun,d1,...,dN)

ci = bootci(nboot,{bootfun,d},Name,Value)

ci = bootci(nboot,{bootfun,d1,...,dN},Name,Value)

[ci,bootstat] = bootci(___)

説明

ci = bootci(nboot,bootfun,d) は、関数 bootfun で計算された各統計量に対する 95% のブートストラップ信頼区間を計算します。関数 bootci は、その計算で nboot ブートストラップ標本を使用し、d の行から復元抽出することで各ブートストラップ標本を作成します。

ci = bootci(nboot,bootfun,d1,...,dN) は、d1,...,dN の非スカラー データ引数の行から復元抽出することで各ブートストラップ標本を作成します。非スカラー引数の行数は同じでなければなりません。関数 bootci は、d1,...,dN の非スカラー データ引数および変更されていないスカラー データ引数の標本を bootfun に渡します。

ci = bootci(nboot,{bootfun,d},Name,Value) では、1 つ以上の名前と値の引数を使用してオプションを指定します。たとえば、名前と値の引数 'Type' を指定して信頼区間のタイプを変更できます。

bootfun および d 引数は単一の cell 配列として bootci に渡さなければならないことに注意してください。

ci = bootci(nboot,{bootfun,d1,...,dN},Name,Value) では、1 つ以上の名前と値の引数を使用してオプションを指定します。たとえば、名前と値の引数 'Alpha' を指定して信頼区間の有意水準を変更できます。

bootfun および d1,...,dN 引数は単一の cell 配列として bootci に渡さなければならないことに注意してください。

[ci,bootstat] = bootci(___) は、前の構文におけるいずれかの入力引数の組み合わせを使用して、nboot ブートストラップのレプリカ標本のそれぞれに対して計算したブートストラップ済み統計量も返します。bootstat の各行は、ブートストラップの標本に bootfun を適用した結果を含みます。

例

ブートストラップ信頼区間

統計的工程管理の能力指数に対する信頼区間を計算します。

平均 1 および標準偏差 1 をもつ正規分布から 30 個の乱数を生成します。

rng('default') % For reproducibility
y = normrnd(1,1,30,1);

工程の下方仕様限界と上方仕様限界を指定します。能力指数を定義します。

LSL = -3;
USL = 3;
capable = @(x)(USL-LSL)./(6*std(x));

2000 個のブートストラップ標本を使用して、能力指数に対する 95% の信頼区間を計算します。既定では、bootci は BCa 法 (bias corrected and accelerated percentile method) を使用して信頼区間を作成します。

ci = bootci(2000,capable,y)

ci = 2×1

    0.5937
    0.9900

能力指数に対するスチューデント化された信頼区間を計算します。

sci = bootci(2000,{capable,y},'Type','student')

sci = 2×1

    0.5193
    0.9930

非線形回帰モデル係数に対するブートストラップ信頼区間

非線形回帰モデルの係数に対するブートストラップ信頼区間を計算します。この例で使用する手法では、予測子と応答の値のブートストラッピングを行い、予測子変数を確率変数と見なします。予測子変数を固定変数と見なし、残差をブートストラッピングする手法については、線形回帰モデル係数に対するブートストラップ信頼区間を参照してください。

メモ: この例では nlinfit を使用します。これは、非線形回帰モデルの係数推定値または残差のみが必要な場合や、ブートストラッピングのようにモデルを複数回繰り返して当てはめる必要がある場合に便利です。当てはめた回帰モデルをさらに調べる必要がある場合は、fitnlm を使用して非線形回帰モデル オブジェクトを作成します。オブジェクト関数 coefCI を使用して結果のモデルの係数に対する信頼区間を作成できますが、この関数ではブートストラッピングは使用しません。

非線形回帰モデル $$y=b_1+b_2\cdot exp(-b_{3}x)+ϵ$$ からデータを生成します。ここで、$$b_1=1$$、$$b_2=3$$ および $$b_3=2$$ は係数です。予測子変数 x は、平均が 2 の指数分布に従います。誤差項 $$ϵ$$ は、平均が 0、標準偏差が 0.1 の正規分布に従います。

modelfun = @(b,x)(b(1)+b(2)*exp(-b(3)*x));

rng('default') % For reproducibility
b = [1;3;2];
x = exprnd(2,100,1);
y = modelfun(b,x) + normrnd(0,0.1,100,1);

beta0 にある初期値を使用する非線形回帰モデルの関数ハンドルを作成します。

beta0 = [2;2;2];
beta = @(predictor,response)nlinfit(predictor,response,modelfun,beta0)

beta = function_handle with value:
    @(predictor,response)nlinfit(predictor,response,modelfun,beta0)

非線形回帰モデルの係数に対する 95% のブートストラップ信頼区間を計算します。生成されたデータ x および y からブートストラップ標本を作成します。

ci = bootci(1000,beta,x,y)

ci = 2×3

    0.9821    2.9552    2.0180
    1.0410    3.1623    2.2695

最初の 2 つの信頼区間には、それぞれ真の係数値 $$b_1=1$$ および $$b_2=3$$ が含まれています。ただし、3 番目の信頼区間には真の係数値 $$b_3=2$$ が含まれていません。

ここで、モデル係数に対する 99% のブートストラップ信頼区間を計算します。

newci = bootci(1000,{beta,x,y},'Alpha',0.01)

newci = 2×3

    0.9730    2.9112    1.9562
    1.0469    3.1876    2.3133

3 つすべての信頼区間に真の係数値が含まれています。

線形回帰モデル係数に対するブートストラップ信頼区間

線形回帰モデルの係数に対するブートストラップ信頼区間を計算します。この例で使用する手法では、残差のブートストラッピングを行い、予測子変数を固定変数と見なします。予測子変数を確率変数と見なし、予測子と応答の値をブートストラッピングする手法については、非線形回帰モデル係数に対するブートストラップ信頼区間を参照してください。

メモ: この例では regress を使用します。これは、回帰モデルの係数推定値または残差のみが必要な場合や、ブートストラッピングのようにモデルを複数回繰り返して当てはめる必要がある場合に便利です。当てはめた回帰モデルをさらに調べる必要がある場合は、fitlm を使用して線形回帰モデル オブジェクトを作成します。オブジェクト関数 coefCI を使用して結果のモデルの係数に対する信頼区間を作成できますが、この関数ではブートストラッピングは使用しません。

標本データを読み込みます。

load hald

線形回帰を実行し、残差を計算します。

x = [ones(size(heat)),ingredients];
y = heat;
b = regress(y,x);
yfit = x*b;
resid = y - yfit;

線形回帰モデルの係数に対する 95% のブートストラップ信頼区間を計算します。残差からブートストラップ標本を作成します。'Type','normal' を指定して、バイアスと標準誤差をブートストラップした正規近似区間を使用します。この場合、既定の信頼区間のタイプは使用できません。

ci = bootci(1000,{@(bootr)regress(yfit+bootr,x),resid}, ...
    'Type','normal')

ci = 2×5

  -47.7130    0.3916   -0.6298   -1.0697   -1.2604
  172.4899    2.7202    1.6495    1.2778    0.9704

切片項を省略して推定された係数 b をプロットし、係数の信頼区間を示す誤差範囲を表示します。

slopes = b(2:end)';
lowerBarLengths = slopes-ci(1,2:end);
upperBarLengths = ci(2,2:end)-slopes;
errorbar(1:4,slopes,lowerBarLengths,upperBarLengths)
xlim([0 5])
title('Coefficient Confidence Intervals')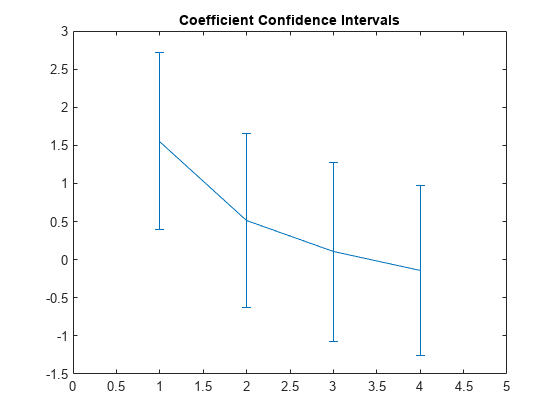

最初の非切片係数のみが 0 と有意に異なります。

複数の統計量に対する信頼区間

100 個のブートストラップ標本の平均値と標準偏差を計算します。各統計量に対する 95% 信頼区間を求めます。

平均 5 をもつ指数分布から 100 個の乱数を生成します。

rng('default') % For reproducibility
y = exprnd(5,100,1);

ベクトル y から 100 個のブートストラップ標本を抽出します。各ブートストラップ標本について平均値と標準偏差を計算します。平均値と標準偏差に対する 95% のブートストラップ信頼区間を求めます。

[ci,bootstat] = bootci(100,@(x)[mean(x) std(x)],y);

ci(:,1) には平均値の信頼区間の下限と上限が格納され、c(:,2) には標準偏差の信頼区間の下限と上限が格納されます。bootstat の各行にはブートストラップ標本の平均値と標準偏差が格納されます。

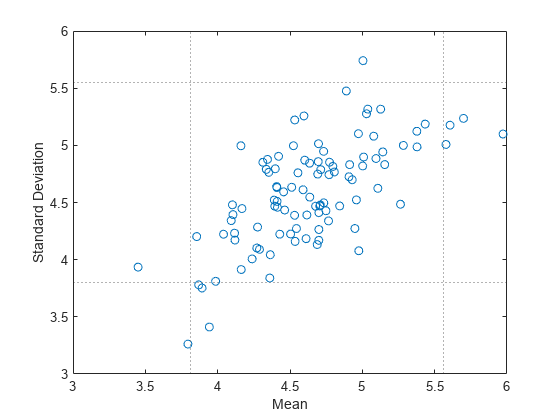
各ブートストラップ標本の平均値と標準偏差を点としてプロットします。平均値の信頼区間の下限と上限を垂直方向の点線としてプロットし、標準偏差の信頼区間の下限と上限を水平方向の点線としてプロットします。

plot(bootstat(:,1),bootstat(:,2),'o')
xline(ci(1,1),':')
xline(ci(2,1),':')
yline(ci(1,2),':')
yline(ci(2,2),':')
xlabel('Mean')
ylabel('Standard Deviation')

入力引数

nboot — ブートストラップ標本の数

正の整数スカラー

ブートストラップ標本の数。正の整数スカラーとして指定します。各ブートストラップ標本を作成するため、bootci によって、d または d1,...,dN 内の n 行の非スカラー データから n 行が復元抽出で無作為に選択されます。

例: 100

データ型: single | double

bootfun — 各標本に適用する関数

関数ハンドル

各標本に適用する関数。関数ハンドルとして指定します。カスタム関数または組み込み関数を指定できます。bootfun は記号 @ を使用して指定しなければなりません。

例: @mean

データ型: function_handle

d — 標本を取得する元のデータ

列ベクトル | 行列

標本を取得する元のデータ。列ベクトルまたは行列として指定します。d の n 行が観測値に対応します。複数のデータ入力引数 d1,...,dN を使用する場合、いくつかの引数をスカラー値として指定することができますが、非スカラー引数の行数はすべて同じでなければなりません。

単一のベクトル引数 d を使用する場合、それを行ベクトルとして指定できます。bootci は次に、ベクトルの要素から標本を抽出します。

データ型: single | double

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: bootci(100,{@mean,1:6'},'Alpha',0.1) は、1 ～ 6 の値から 100 個のブートストラップ標本を抽出し、各標本の平均を取り、次に標本の平均値に対して 90% の信頼区間を計算するように指定します。

Alpha — 有意水準

0.05 (既定値) | (0,1) の正のスカラー

有意水準。0 ～ 1 の正のスカラーを指定します。bootci は、関数 bootfun で定義される各統計量の 100*(1-Alpha) ブートストラップ信頼区間を計算します。

例: 'Alpha',0.01

データ型: single | double

Type — 信頼区間のタイプ

'bca' (既定値) | 'norm' | 'per' | 'cper' | 'stud' | ...

信頼区間のタイプ。次の表のいずれかの値を指定します。

値	説明
'norm' または 'normal'	バイアスと標準誤差をブートストラップした正規近似区間[1]
'per' または 'percentile'	基本の等百分位数法
'cper' または 'corrected percentile'	バイアス補正百分位数法[2]
'bca'	BCa 法 (bias corrected and accelerated percentile method) [3]、[4]。この方法には、元の標本値未満のブートストラップ値の比率を使用して計算される z0 係数が含まれます。標本が塊状の場合に合理的な結果を得るために、z0 は元の標本値と同じブートストラップ値の半分を含めることで計算されます。
'stud' または 'student'	スチューデント化された信頼区間[3]

例: 'Type','student'

NBootStd — スチューデント化された標準誤差推定用のブートストラップ標本の数

100 (既定値) | 正の整数スカラー

スチューデント化された標準誤差推定用のブートストラップ標本の数。正の整数スカラーとして指定します。

bootci は、関数 bootfun で定義される統計量のスチューデント化されたブートストラップ信頼区間を計算し、NBootStd 個のブートストラップ データ標本を使用してブートストラップ統計量の標準誤差を推定します。

メモ

この名前と値の引数を使用するには、Type の値が 'stud' または 'student' でなければなりません。NBootStd と StdErr の両方ではなく、いずれかを指定してください。

例: 'NBootStd',50

データ型: single | double

StdErr — スチューデント化された標準誤差推定の計算に使用する関数

関数ハンドル

スチューデント化された標準誤差推定の計算に使用する関数。関数ハンドルを指定します。

bootci は、関数 bootfun で定義される統計量のスチューデント化されたブートストラップ信頼区間を計算し、関数 StdErr を使用してブートストラップ統計量の標準誤差を推定します。関数 StdErr は、bootfun と同じ引数をとらなければならないため、bootfun で計算された統計量の標準誤差が返されます。

メモ

この名前と値の引数を使用するには、Type の値が 'stud' または 'student' でなければなりません。NBootStd と StdErr の両方ではなく、いずれかを指定してください。

例: 'StdErr',@std

データ型: function_handle

Weights — 観測値の重み

ones(n,1)/n (既定値) | 非負のベクトル

観測値の重み。正の要素を 1 つ以上含む非負のベクトルを指定します。Weights の要素数は、d または d1,...,dN のデータの行数 n と等しくなければなりません。1 つのブートストラップ標本を取得するために、bootci は、多項分布抽出確率としてこれらの重みを使用し、n 行のデータから n 行を復元抽出で無作為に選択します。

データ型: single | double

Options — 並列計算と乱数ストリーム設定のオプション

構造体

並列計算と乱数ストリーム設定のオプション。構造体として指定します。statset を使用して Options 構造体を作成します。次の表は、オプションのフィールドとその値の一覧です。

フィールド名	値	既定の設定
UseParallel	並列計算を行う場合は、この値を true に設定します。	false
UseSubstreams	再現可能な方法で計算する場合は、この値を true に設定します。 再現性のある計算を行うには、Streams をサブストリームを許可する型 ("mlfg6331_64" または "mrg32k3a") に設定します。	false
Streams	RandStream オブジェクトまたはそのようなオブジェクトの cell 配列としてこの値を指定します。UseParallel の値が true でなく、UseSubstreams の値も false でない場合、単一オブジェクトを使用します。この場合は、並列プールと同じサイズの cell 配列を使用します。	Streams を指定しなかった場合、bootci は既定のストリームを使用します。

メモ

並列計算を行うには、Parallel Computing Toolbox™ が必要です。

例: Options=statset(UseParallel=true,UseSubstreams=true,Streams=RandStream("mlfg6331_64"))

データ型: struct

出力引数

ci — 信頼区間の範囲

2 行のベクトル | 2 行の行列 | 2 行の多次元配列

信頼区間の範囲。2 行のベクトル、行列または多次元配列として返されます。

• ci が信頼区間の上限および下限を含んでいるベクトルの場合、bootfun はスカラーを返します。

• bootfun が長さ m のベクトルを返す場合、ci はサイズ 2 行 m 列の行列になります。ここで、ci(1,:) は下限で、ci(2,:) は上限です。

• bootfun が多次元配列を返す場合、ci は配列になります。ここで、ci(1,:,...) は下限の配列で、ci(2,:,...) は上限の配列です。

bootstat — ブートストラップ統計量

列ベクトル | 行列

ブートストラップ統計量。nboot 行の列ベクトルまたは行列として返されます。bootstat の i 番目の行は、i 番目のブートストラップ標本に bootfun を適用した結果に対応します。bootfun が行列または配列を返す場合、関数 bootci はこの出力を bootstat に保存する前に行ベクトルに変換します。

参照

[1] Davison, A. C., and D. V. Hinkley. Bootstrap Methods and Their Applications. Cambridge University Press, 1997.

[2] Efron, Bradley. The Jackknife, the Bootstrap and Other Resampling Plans. Philadelphia: The Society for Industrial and Applied Mathematics, 1982.

[3] DiCiccio, Thomas J., and Bradley Efron. “Bootstrap Confidence Intervals.” Statistical Science 11, no. 3 (1996): 189–228.

[4] Efron, Bradley, and Robert J. Tibshirani. An Introduction to the Bootstrap. New York: Chapman & Hall, 1993.

拡張機能

自動並列サポート

Parallel Computing Toolbox™ を使用して自動的に並列計算を実行することで、コードを高速化します。

並列実行するには、この関数を呼び出すときに名前と値の引数 Options を指定し、statset を使用してオプション構造体の UseParallel フィールドを true に設定します。

Options=statset(UseParallel=true)

並列計算の詳細については、自動並列サポートを使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a で導入

参考

bootstrp | jackknife | statget | statset | randsample | parfor

トピック

• 統計標本のリサンプリング