動くビリヤードボールのダイナミクスのモデル化

この例では次を使用します。

この例では、連続時間の行列変数を使用してビリヤードゲームのオープニングショットをモデル化する方法を説明します。モデルの Stateflow® チャートは、大量の不連続点をもつハイブリッドシステムのダイナミクスをシミュレートします。詳細については、Stateflow の連続時間モデルを参照してください。

シミュレーションを開始すると、MATLAB® ユーザーインターフェイス (UI) には、三角形の枠に 15 個のビリヤードボールが配置されたビリヤードテーブルが表示されます。次に、キューボールの最初の位置と速度を選択することを求めるプロンプトが UI に表示されます。キューボールが放たれると、高速で衝突し続けるビリヤードボールの動きが UI によってアニメーション化されます。

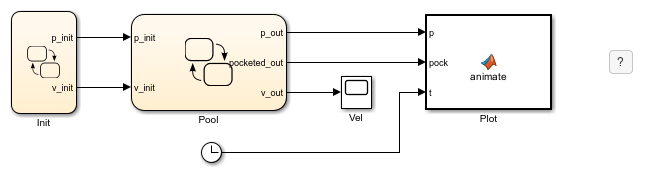
モデルは次のもので構成されています。

Stateflow チャート Init。関数 sf_pool_plotter.m を呼び出し、UI からの入力に基づいてキューボールの位置と速度を初期化します。
Stateflow チャート Pool。各ビリヤードボールの 2 次元のダイナミクスを計算します。
MATLAB Function ブロック Plot。関数 sf_pool_plotter.m を呼び出し、シミュレーション中のビリヤードボールの動きをアニメーション化します。
Scope ブロック Vel。オープニングショット中の各ビリヤードボールの速度を表示します。

連続時間ダイナミクスの計算

ビリヤードボールのダイナミクスを表すため、Pool チャートはいくつかの仮定を行います。

連続時間変数

システムの状態がボールの位置と速度によって完全に記述されるよう、チャートはボールのスピンを無視します。各ボールが単位質量をもつと仮定されるので、その位置と速度は次の微分方程式系によって記述されます。

$
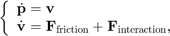
\left\{ \begin{array}{ll}
\dot{\mathbf{p}} = \mathbf{v} \\
\dot{\mathbf{v}} = \mathbf{F}_\mathrm{friction} +
\mathbf{F}_\mathrm{interaction},
\end{array} \right.
$

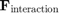ここで $\mathbf{F}_\mathrm{friction}$ と $\mathbf{F}_\mathrm{interaction}$ は、ビリヤードテーブルとの摩擦による力と、他のボールとの衝突によって発生する力です。

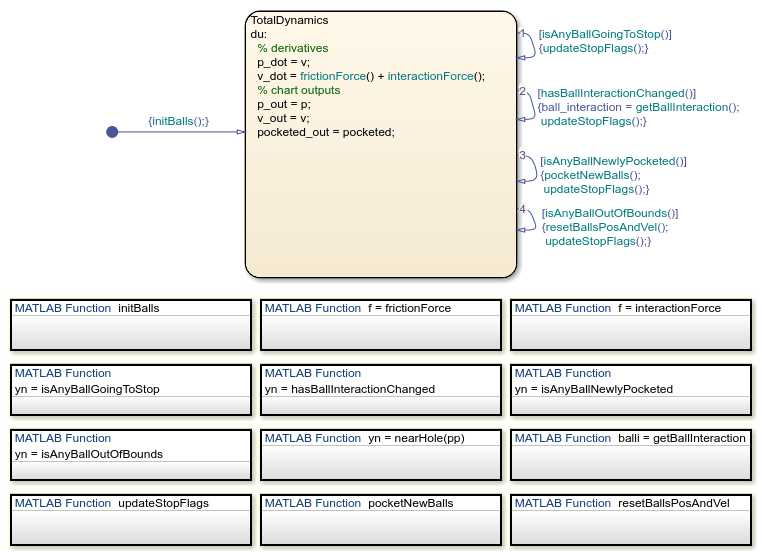
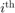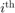ボールの位置と速度を追跡するため、チャートは 16 行 2 列の行列のペアを連続時間変数 p と v に保存します。各行列で、 $i^\mathrm{th}$ 行は $i^\mathrm{th}$ ボールの 2 次元の位置または速度を表します。

摩擦モデル

各ボールに作用する摩擦力を計算するため、チャートは MATLAB 関数 frictionForce を呼び出します。この関数は簡略化された摩擦モデルを実装します。摩擦はそれぞれの動くボールに対し、動きの反対方向に一定の力で作用します。摩擦は静止しているボールには作用しないので、各ボールへの摩擦力は本質的にモーダルです。

$
\mathbf{F}_\mathrm{friction} =
\left\{ \begin{array}{ll}
-\mu g \displaystyle\frac{\mathbf{v}}{\|\mathbf{v}\|}
& \|\mathbf{v}\|>0 \\
0 & \mathrm{otherwise,}
\end{array} \right.
$

ここで $\mu$ は摩擦係数、は重力加速度です。

衝突ダイナミクス

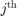ボール間の衝突によって起きる相互作用を特定するため、チャートは MATLAB 関数 interactionForce を呼び出します。この関数は 2 つのボールが互いに接触するときの単純な復元力モデルを実装します。 $i^\mathrm{th}$ と $j^\mathrm{th}$ のボール間の相互作用力はモーダルです。

$
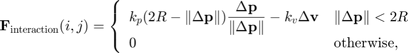
\mathbf{F}_{\mathrm{interaction}}(i,j) =
\left\{ \begin{array}{ll}
k_p (2R-\|\Delta \mathbf{p}\|)
\displaystyle\frac{\Delta \mathbf{p}}{\|\Delta \mathbf{p}\|}
- k_v\Delta \mathbf{v} & \|\Delta \mathbf{p}\| < 2R \\
0 & \mathrm{otherwise,}
\end{array} \right.
$

ここで、

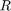は各ボールの半径。
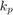および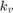は弾性定数。
$\Delta \mathbf{p} = \mathbf{p}_i - \mathbf{p}_j$ は 2 つのボールの中心の相対距離。
$\Delta \mathbf{v} = \mathbf{v}_i - \mathbf{v}_j$ は 2 つのボールの相対速度。

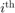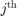ボールは 2 次元で自由に移動するため、チャートは 16 行 16 列の boolean 行列 ball_interaction を使用してすべての潜在的な衝突を考慮します。たとえば、 $i^\mathrm{th}$ と $j^\mathrm{th}$ のボールが接触している場合、ball_interaction(i,j) の値は true です。それ以外の場合、この値は false です。衝突は本来対称なので、チャートは行列の上三角部分のみを使用します。

MATLAB 関数での行列計算の実行

ビリヤードボールの 2 次元ダイナミクスを計算するため、Pool チャートは行列計算を実行するいくつかの MATLAB 関数を呼び出します。

initBalls は、ビリヤードテーブル上の各ボールの位置と速度を初期化します。
frictionForce は、各ボールにかかる摩擦力を計算します。
interactionForce は、各ボールにかかる相互作用力を計算します。
isAnyBallGoingToStop は、いずれかのボールが動きを止めると 1 の値を返します。それ以外の場合、関数は 0 の値を返します。
hasBallInteractionChanged は、いずれかのボールの相互作用が変化すると 1 の値を返します。それ以外の場合、関数は 0 の値を返します。
isAnyBallNewlyPocketed は、いずれかのボールがポケットに落ちると 1 の値を返します。それ以外の場合、関数は 0 の値を返します。
isAnyBallOutOfBounds は、いずれかのボールがビリヤードテーブルの境界の外にある場合に true の値を返します。それ以外の場合、関数は false の値を返します。
nearHole は、ボールがビリヤードテーブルのポケットの近くにある場合に true の値を返します。それ以外の場合、関数は false の値を返します。
getBallInteraction は、いずれかのボールが互いに接触しているかどうかを指定する boolean 行列を返します。
updateStopFlags は、どのボールの動きが止まったかを追跡し、ベクトル stopped に結果を保存します。
pocketNewBalls は、ポケットに入った各ボールの速度を 0 に設定します。
resetBallsPosAndVel は、ビリヤードテーブルの境界の外にあるすべてのボールの位置と速度をリセットします。

シミュレーション結果の表示

シミュレーションの開始に際し、UI にはビリヤードテーブルと、15 個のビリヤードボールが台の片側に並んで表示されます。キューボールの最初の位置を指定するには、ビリヤードテーブルの任意の場所をクリックします。

突き玉の最初の速度を指定するには、ビリヤードテーブルの別の場所をクリックします。

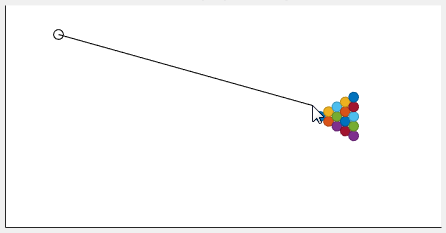
モデルはシステムのダイナミクスをシミュレートして、ビリヤードボールの動きをアニメーション化します。

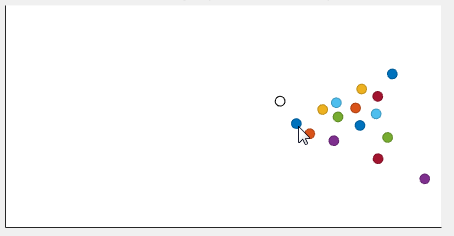
シミュレーションを停止するには、UI を閉じます。

動くビリヤード ボールのダイナミクスのモデル化

連続時間ダイナミクスの計算

MATLAB 関数での行列計算の実行

シミュレーション結果の表示

関連するトピック

動くビリヤードボールのダイナミクスのモデル化