回転の測定
回転検出の概要
座標系の回転は各種の形式で測定できます。これらには軸角度、四元数、変換、回転シーケンスが含まれます。各種の形式は、Transform Sensor ブロックを介して利用できます。また、限定的ながらジョイント ブロックでも利用できます。選択する測定形式はモデルによって異なります。用途に最適な形式を選択してください。
回転の測定
回転は相対量です。1 つの座標系の回転は、別の座標系に対してのみ意味があります。したがって、回転検出機能をもつブロックで測定を実行するには、測定座標系と基準座標系の 2 つの座標系が必要です。このようなブロックでは、follower 座標系端子が測定座標系を特定し、base 座標系端子が測定の基準座標系を特定します。
Simscape™ Multibody™ は、標準的な規則に従って回転形式を定義します。場合によっては、複数の規則が存在します。これは、四元数の場合などに当てはまります。回転の測定を正しく解釈するには、回転形式の定義を見直してください。
軸角度測定
軸角度は、比較的単純な測定形式です。この形式では、軸ベクトルと角度という 2 つのパラメーターを使用して回転を完全に表します。軸角度形式の有用性は、オイラーの回転定理から直接導かれます。この定理によると、3 次元回転または回転シーケンスは、固定された 1 つの軸の周りを回る、純粋な回転として表すことができます。

座標系の回転を軸角度形式で測定するには、Transform Sensor ブロックを使用します。ブロックのプロパティ インスペクターには、別々に [Axis] パラメーターと [Angle] パラメーターがあり、これらを選択することによって、対応する物理量信号 (PS) 端子 (それぞれ axs と q というラベル) を表示できます。軸と角度のパラメーターは独立して表示されるため、軸、角度またはその両方の測定を選択できます。
軸の出力は、[ax, ay, az] という形式の 3D 単位ベクトルです。この単位ベクトルは、回転方向を右手の法則に従って符号化します。たとえば、+X 軸の周りを反時計方向に回る座標系の回転軸は [1 0 0] です。同じ軸の周りを時計方向に回る座標系の回転軸は [-1 0 0] です。
角度出力は、範囲 0 ~ π のスカラーの数値です。この数値は、測定軸の周りを回転する範囲を符号化します。既定では、角度はラジアン単位で測定されます。角度単位は、Simulink® ブロックとのインターフェイスに使用されている PS-Simulink Converter ブロックで変更できます。
四元数の測定
四元数は、多元数に基づく回転の表現です。四元数は、スカラー部分 S とベクトル部分 V で構成されています。スカラー部分は回転の角度を符号化し、ベクトル部分は回転軸を符号化します。
四元数の主な利点は、特異点のないパラメーター空間です。オイラー角のシーケンスに存在する数学的特異点は、回転自由度の喪失につながります。この現象は、ジンバル ロックとして知られています。Simscape Multibody では、ジンバル ロックは数値誤差を発生させ、シミュレーションの失敗の原因になります。特異点が存在しないということは、シミュレーション目的には四元数がよりロバストであることを意味します。
座標系の回転を四元数形式で測定するには、次を使用します。
A Transform Sensor ブロック (2 つの一般的な座標系間の回転を測定する場合)。プロパティ インスペクターの [Rotation] メニューには [Quaternion] パラメーターがあり、これを選択することによって、対応する物理量信号端子 ([Q] というラベル) を表示できます。
球面プリミティブをもつジョイント ブロック (2 つのジョイント座標系間の 3 次元回転を測定する場合)。プロパティ インスペクターの [Sensing] メニューには [Position] パラメーターがあり、これを選択することによって、対応する物理量信号端子 (これも [Q] というラベル) を表示できます。詳細については、Spherical Joint ブロックのリファレンス ページを参照してください。
四元数出力は、4 要素の行ベクトル です。ここで、
および
θ は回転の角度であり、[Ux, Uy, Uz] は回転軸の単位ベクトルです。任意の回転に対して、2 つの四元数があることに注意してください。それらは互いに逆向きですが、同じ回転を表します。たとえば、四元数 [1 0 0 0] と [-1 0 0 0] は、いずれも恒等回転を表します。
変換の測定
回転変換は、座標系の回転を符号化する 3×3 行列です。base 座標系の軸 [x, y, z]B に関して、follower 座標系の軸 [x, y, z]F は次の関係にあります。
それぞれの行列の列には、base 座標系で表現される、follower 座標系の軸の座標が含まれます。たとえば、最初の列は、follower 座標系の x 軸を base 座標系内で表現した座標を示します。同様に、2 番目と 3 番目の列には、y 軸と z 軸の座標がそれぞれ含まれます。回転行列を使用したベクトル操作では、ベクトルの座標が、follower 座標系から base 座標系に変換されます。
Transform Sensor ブロックを使用して、座標系の回転を回転行列として検出できます。このブロックのプロパティ インスペクターには [Transform] オプションがあり、これを選択すると、R というラベルの付いた物理量信号端子が表示されます。この端子を使用して回転行列信号を出力し、PS-Simulink Converter ブロックでその出力物理量信号を Simulink 信号に変換した後、Simulink サブシステムで処理や解析などを行います。
回転シーケンスの測定
回転シーケンスの測定では、座標系の軸を中心とする 3 つの連続した基本回転を使用して 2 つの座標系間の向きの違いを表します。回転シーケンスの測定を使用するには、sequenceAngles メソッドまたは Transform Sensor ブロックの [Rotation Sequence] パラメーターを使用します。
基本回転は、各基本回転の後にその向きが変わる中間座標系を中心とする場合は内因性となります。基本回転の中心が固定の座標系の場合は外因性の回転となります。測定には、X-Y-X、X-Y-Z、X-Z-X、X-Z-Y、Y-X-Y、Y-X-Z、Y-Z-X、Y-Z-Y、Z-X-Y、Z-X-Z、Z-Y-X、および Z-Y-Z の 12 種類の回転シーケンスがあります。Transform Sensor ブロックの端子 seq からの出力は内因性回転の角度であることに注意してください。Z-Y-Z シーケンスに基づく 3 つの内因性回転をもつ 3 次元回転を表す例を図に示します。
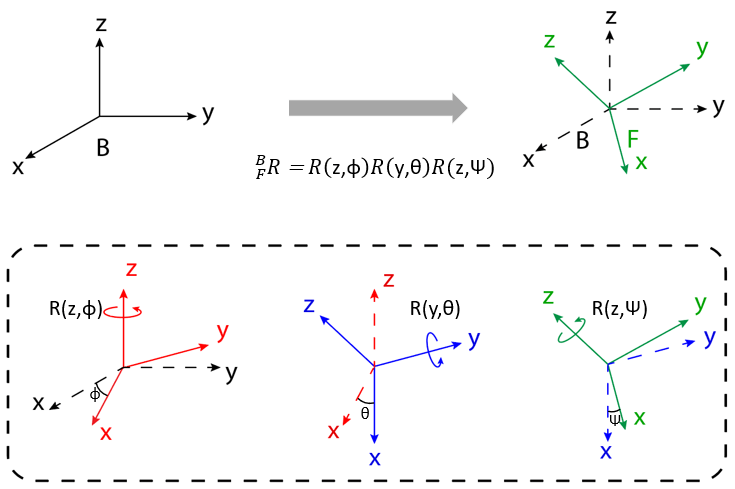
外因性回転は同じ角度の内因性回転と等価ですが、シーケンスの順序が逆です。たとえば、角度 φ、θ、Ψ による外因性回転 Z-Y-X は、角度 Ψ、θ、φ による内因性回転 X-Y-Z と等価です。
回転にジンバル ロックなどのロックの問題がなければ、回転シーケンスの測定には 2 セットの解が存在しますが、Transform Sensor ブロックまたは sequenceAngles メソッドではそのうちの 1 セットのみが出力されます。3 つの角度の範囲はいずれも [-π, π] です。X-Y-Z や Z-X-Y のように、回転シーケンスの文字が異なる場合は、2 番目の回転角度の範囲が (-π/2, π/2) になります。X-Y-X や Z-Y-Z のように、回転シーケンスの最初と最後の文字が同じ場合は、2 番目の回転角度の範囲が (0, π) になります。
次の場合はロックの問題が発生し、最初と最後の回転角度の解が無限に存在します。
回転シーケンスの文字が異なり、2 番目の回転角度が-π/2 または π/2 に等しい。
回転シーケンスの最初と最後の文字が同じで、2 番目の回転角度が 0 または π に等しい。
これらの場合、Transform Sensor ブロックまたは sequenceAngles メソッドは、最初と最後の角度の大きさが同じである 1 セットの解のみを出力します。