このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

計算遅延とサンプリングの効果のモデル化

この例では、Simulink® Control Design™ を使用して計算遅延とサンプリングの効果をモデル化する方法を説明します。

計算遅延とサンプリング効果は、制御システムの性能に大きな影響を与える可能性があります。通常、これらの要素を考慮しなければ、システムの閉ループ応答は、振動して不安定になります。したがって、制御システムをモデル化する場合、計算遅延とサンプリング効果を考えて、閉ループ システムを正確に設計してシミュレートする必要があります。

計算遅延とサンプリングの効果を使用して、補償器を設計する方法は 2 つあります。1 つ目は、離散領域でコントローラーを設計し、プラントを離散化することでサンプリングの効果を得る方法です。2 つ目は、連続領域でコントローラーを設計する方法です。後者の方法が便利なときもありますが、この場合は、計算遅延とサンプリングの効果を考慮する必要があります。この例では、両方の方法を適用し、Simulink Control Design ソフトウェアを使用して制御システムを再設計します。

離散コントローラーと連続コントローラーのシミュレーション

次のモデル例では、当初の補償器に単ループのフィードバック/プレフィルターの補償器設計の例における補償器からの次のゲインがあります。

P = 0.0018222
I = 0.0052662

最初のモデルには、制御システムの離散的実装があります。

mdl = 'scdspeed_compdelay';
open_system(mdl)

このモデルでは、Computational Delay ブロックは計算遅延の効果をモデル化します。遅延は、コントローラーのサンプル時間に等しく、これは最悪の場合です。Zero-Order Hold ブロックは、システムの応答に対するサンプリングの効果をモデル化します。最後に、速度コントローラー (PID Controller ブロックを使用して実装) は、前進オイラー サンプリング法を使用して離散化されます。

サンプリングの効果は、システムの応答をシミュレートすることで確認できます。

最初に、コントローラーをサンプル時間 Ts = 0.1 秒で離散化してモデルをシミュレートします。

Ts = 0.1;
sim(mdl);
T2 = simout.time;
Y2 = simout.signals.values;

次に、サンプル時間を Ts = 0.25 秒にしてモデルをシミュレートします。

Ts = 0.25;
sim(mdl);
T3 = simout.time;
Y3 = simout.signals.values;

2 つ目のモデルは、連続モデルです。

mdl_continuous = 'scdspeed_contcomp';
open_system(mdl_continuous)

連続モデルの応答をシミュレートします。

sim(mdl_continuous);
T1 = simout.time;
Y1 = simout.signals.values;

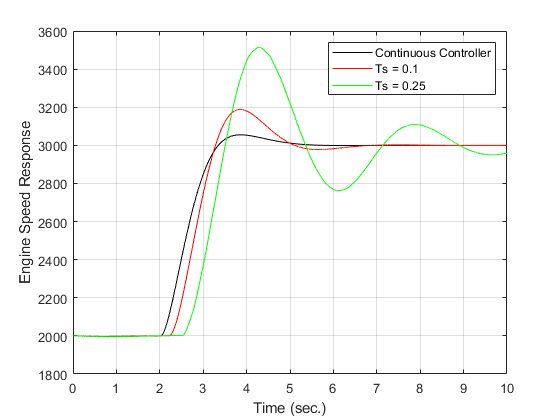
離散モデルと連続モデルの両方のシミュレーションをプロットします。サンプル時間を大きくすると応答の振動が大きくなります。

plot(T1,Y1,'k',T2,Y2,'r',T3,Y3,'g')
xlabel('Time (sec.)')
ylabel('Engine Speed Response')
legend('Continuous Controller','Ts = 0.1','Ts = 0.25')
grid

離散領域での補償器の設計

一番遅いサンプル時間 (Ts = 0.25) を使用して、閉ループ システムの振動効果を取り除くには、補償器を再設計する必要があります。

最初に、プラントの離散化したバージョンを使用してコントローラーを再設計します。単ループのフィードバック/プレフィルターの補償器設計と同様の方法で補償器を再設計できます。調整した補償器のゲインは次のとおりです。

P = 0.00066155
I = 0.0019118795

set_param('scdspeed_compdelay/PID Controller','P','0.00066155')
set_param('scdspeed_compdelay/PID Controller','I','0.0019118795')

結果の閉ループ システムをサンプル時間 Ts = 0.25 秒でシミュレートします。これらの結果について、この例の後の手順で調べます。

Ts = 0.25;
sim(mdl);
Td = simout.time;
Yd = simout.signals.values;

連続領域での遅延とサンプリングの考慮

2 つ目の方法として、単位遅延とゼロ次ホールドの連続等価を使用してコントローラーを再設計します。

この例では、ゼロ次ホールドのダイナミクスとして以下を使用します。

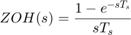
これらのダイナミクスをモデルで指定するには、Zero-Order Hold ブロックを右クリックし、[線形解析]、[選択したブロック線形化を指定] を選択します。[ブロックの線形化] ダイアログ ボックスで、ゼロ次ホールドのダイナミクスの式を指定します。

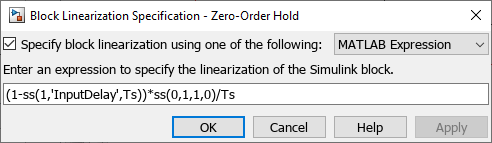
または、次のコードを使用してブロックの線形化を指定することもできます。

zohblk = 'scdspeed_compdelay/Zero-Order Hold';
set_param(zohblk,'SCDEnableBlockLinearizationSpecification','on')
rep = struct('Specification','(1-ss(1,''InputDelay'',Ts))*ss(0,1,1,0)/Ts',...
             'Type','Expression',...
             'ParameterNames','',...
             'ParameterValues','');
set_param(zohblk,'SCDBlockLinearizationSpecification',rep)

連続伝達遅延を使用して Computational Delay ブロックの線形化を指定します。

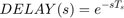
次のコードを使用して遅延ブロックの線形化を指定します。

delayblk = 'scdspeed_compdelay/Computational Delay';
set_param(delayblk,'SCDEnableBlockLinearizationSpecification','on')
rep = struct('Specification','ss(1,''InputDelay'',Ts)',...
             'Type','Expression',...
             'ParameterNames','',...
             'ParameterValues','');
set_param(delayblk,'SCDBlockLinearizationSpecification',rep)

遅延とサンプリングの効果の連続時間モデルで、コントローラー設計の解析は連続領域に残ります。

次に、Ts = 0.1 秒および 0.25 秒の遅延を使用してモデルを線形化します。これを行うには、まず入力と出力の線形解析ポイントを設定します。

io(1) = linio('scdspeed_compdelay/PID Controller',1,'input');
io(2) = linio('scdspeed_compdelay/Zero-Order Hold',1,'openoutput');

モデルを Ts = 0.1 で線形化します。

Ts = 0.1;
sys2 = linearize(mdl,io);

モデルを Ts = 0.25 で線形化します。

Ts = 0.25;
sys3 = linearize(mdl,io);

最後に、サンプリングおよび計算遅延の効果を使用しないで、モデルを線形化します。

io(1) = linio('scdspeed_contcomp/PID Controller',1,'input');
io(2) = linio('scdspeed_contcomp/rad//s to rpm',1,'openoutput');
sys1 = linearize(mdl_continuous,io);

エンジンの線形モデルを使用すると、周波数応答に対する計算遅延の効果を調べることができます。この場合、システムの位相応答は、サンプリングによって導入された遅延により大幅に減少します。

p = bodeoptions('cstprefs');
p.Grid = 'on';
p.PhaseMatching = 'on';
bodeplot(sys1,'k',sys2,'r',sys3,'g', {1e-2,1e2},p)
legend('Continuous Model','Ts = 0.1','Ts = 0.25','Location','southwest')

一番遅いサンプル時間でモデルを使用して、単ループのフィードバック/プレフィルターの補償器設計の手法で補償器を再設計します。そうすることにより、次の PI ゲインが得られます。

P = 0.00065912
I = 0.001898342

これらのゲインをコントローラーで設定します。

set_param('scdspeed_compdelay/PID Controller','P','0.00065912')
set_param('scdspeed_compdelay/PID Controller','I','0.001898342')

結果の閉ループ システムをサンプル時間 Ts = 0.25 でシミュレートします。

sim(mdl)
Tc = simout.time;
Yc = simout.signals.values;

応答の比較

設計の応答をプロットします。両方の方法を使用して制御システムを再設計すると、同様のコントローラーが得られます。この例では、計算遅延と離散化の効果を示します。これらの効果により、システムの安定余裕は減少しますが、制御システムを適切にモデル化すると、目的の閉ループ動作を実現できます。

plot(T1,Y1,'k',T3,Y3,'b',Td,Yd,'m',Tc,Yc,'r')
xlabel('Time (sec.)')
ylabel('Engine Speed Response')
legend('Continuous compensator (original)','Discrete compensator (original)', ...
    'Discrete compensator (discrete redesign)',...
    'Discrete compensator (continuous redesign)',...
    'Location','southeast')
grid

bdclose('scdspeed_contcomp')
bdclose('scdspeed_compdelay')

参考

制御システム デザイナー

関連するトピック

• むだ時間をもつプラントの補償器設計
• 制御システム デザイナーの調整法
• 単ループのフィードバック/プレフィルターの補償器設計