モデル規範形適応制御

Model Reference Adaptive Control ブロックは、不確かさをもつ制御対象システムを特定の参照プラント モデルの動作に追従させる制御動作を計算します。このブロックを使用して、次のモデル規範形適応制御 (MRAC) アルゴリズムを実装できます。

• 直接 MRAC — 参照プラント モデルと制御対象システムの状態のリアルタイムの追従誤差に基づいて、フィードバック コントローラーとフィードフォワード コントローラーのゲインを推定します。

• 間接 MRAC — 参照プラント モデルと推定されるシステムの状態の追従誤差に基づいて、制御対象システムのパラメーターを推定します。その後、推定されるシステムと参照モデルのパラメーターに基づいて、フィードバック コントローラーとフィードフォワード コントローラーのゲインを派生させます。

MRAC では、直接と間接のどちらでも、さらに制御対象システムの外乱と不確かさのモデルを推定します。コントローラーは制御動作を計算する際に、このモデルを使用して外乱と不確かさを補正します。

いずれの場合も、コントローラーは、推定されたパラメーターと外乱モデルを追従誤差に基づいてリアルタイムで更新します。

参照モデル

直接と間接のどちらの MRAC でも、参照プラント モデルは次のようになります。これは、実際に達成する目標の動作を特徴付ける理想的なシステムを示します。

$${\dot{x}}_m\left(t\right)=A_m{x}_m\left(t\right)+B_{m}r\left(t\right)$$

ここで

• r(t) は外部基準信号です。

• x_m(t) は参照プラント モデルの状態です。r(t) がわかっているため、参照モデルをシミュレートして x_m(t) を取得できます。

• A_m は定数の状態行列です。安定した参照モデルの場合、A_m はすべての固有値が厳密に負の実数部をもつフルビッツ行列でなければなりません。

• B_m は制御有効行列です。

外乱と不確かさのモデル

Model Reference Adaptive Control ブロックは、制御対象システムの外乱とモデルの不確かさを内部モデル u_ad として保持します。

$$u_{ad}=w^T\varphi \left(x\right)$$

ここで、ϕ(x) はモデルの特徴のベクトルです。w は、コントローラーが追従誤差に基づいてリアルタイムで更新する適応制御の重みベクトルです。

ϕ(x) の定義には、次のいずれかの特徴の定義を使用できます。

• 制御対象プラントの状態ベクトル — この方法では、システムの不確かさが十分に表現されないことがあります。状態を特徴として使用すると、外乱とモデルの不確かさの複雑度がわからない場合の開始点として便利です。

• ガウス放射基底関数 — このオプションは、外乱とモデルの不確かさが非線形であり、外乱モデルの構造がわからない場合に使用します。放射基底関数では、モデルの演算領域の事前知識が必要ですが、一部のケースではこれは困難な場合があります。

• 単一の隠れ層ニューラル ネットワーク — このオプションは、外乱とモデルの不確かさが非線形であり、外乱モデルの構造がわからず、演算領域の事前知識がない場合に使用します。ニューラル ネットワークは、任意の連続関数を近似できる汎用関数近似器です。

• コントローラー ブロックに提供される外部ソース — このオプションは、独自のカスタム特徴ベクトルを定義する場合に使用します。このオプションは外乱と不確かさのモデルの構造がわかっている場合に使用できます。たとえば、カスタム特徴ベクトルを使用することで特定の不明なプラント パラメーターを識別できます。

直接 MRAC

直接 MRAC コントローラーの制御構造は次のとおりです。

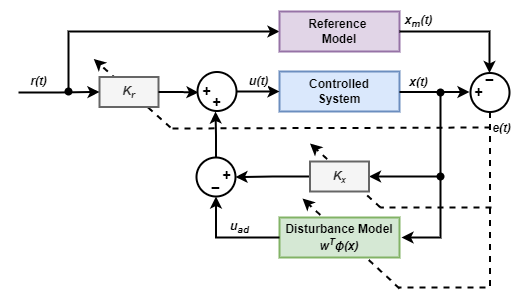
コントローラーは、制御入力 u(t) を次のように計算します。

$$\begin{array}{l}u\left(t\right)=k_{x}x\left(t\right)+k_{r}r\left(t\right)-u_{ad}\\ u_{ad}=w^T\varphi \left(x\right)\end{array}$$

ここで

• x(t) は制御対象システムの状態です。

• r(t) は外部基準信号です。

• k_x と k_r はフィードバック コントローラーとフィードフォワード コントローラーのゲインです。

• u_ad は外乱モデルから派生する適応制御コンポーネントです。

  ϕ(x) には外乱モデルの特徴が含まれます。

• w は適応外乱モデルの重みベクトルです。

• V は隠れ層重みベクトルです。

単一の隠れ層ニューラル ネットワークでは、u_ad は次のとおりです。

$$u_{ad}=w^T\sigma \left(V^{T}x\right)$$

ここで

• V は隠れ層重みベクトルです。

• σ はシグモイド活性化関数です。

コントローラーは、制御対象システムの状態と参照モデルの状態の誤差 e(t) を計算します。その後、その誤差を使用して k_x、k_r、および w の値をリアルタイムで適応させます。

ノミナル モデル

制御対象システムには、一般にモデル化の不確かさと外乱があります。制御対象システムのノミナルの状態方程式を次に示します。コントローラーは、この想定されるノミナルのプラント動作をコントローラーのパラメーターの更新時に使用します。

$$\dot{x}\left(t\right)=Ax\left(t\right)+B\left(u\left(t\right)+f\left(x\right)\right)$$

ここで

• x(t) は制御するシステムの状態です。

• u(t) は制御入力です。

• A は定数の状態遷移行列です。

• B は定数の制御有効行列です。

• f(x) はシステム内の一致する不確かさです。

パラメーターの更新

直接 MRAC コントローラーは、次の方程式を使用して、状態ベクトル、放射基底関数、および外部ソースの特徴の定義のためにコントローラーのゲインと外乱モデルの重みを更新します [1] [2]。

$$\begin{array}{l}{\dot{k}}_x={\Gamma }_{x}x\left(t\right)e^T\left(t\right)PB\\ {\dot{k}}_r={\Gamma }_{r}r\left(t\right)e^T\left(t\right)PB\\ \dot{w}={\Gamma }_w\varphi \left(x\right)e^T\left(t\right)PB\end{array}$$

単一の隠れ層外乱モデルの更新方程式では、以下の更新方程式とともに同じコントローラーのゲインの更新を使用します。

$$\begin{array}{l}\dot{w}=-\left(\sigma \left(V^{T}x\right)-{\sigma }^{\prime }\left(V^{T}x\right)V^{T}x\right)e^T\left(t\right)PB{\Gamma }_w\\ \dot{V}=-{\Gamma }_{V}x{e}^T\left(t\right)PB{w}^T\sigma \left(V^{T}x\right)\end{array}$$

ここで、P は参照モデルの状態行列に基づく次のリアプノフ関数の解、B はノミナル プラント モデルからの制御有効行列です。

$$A_m^{T}P+P{A}_m+Q=0$$

ここで、Q はサイズが N 行 N 列の正定値行列です。N は状態ベクトル x(t) のサイズです。

間接 MRAC

間接 MRAC コントローラーの制御構造は次のとおりです。参照モデルは次のようになります。

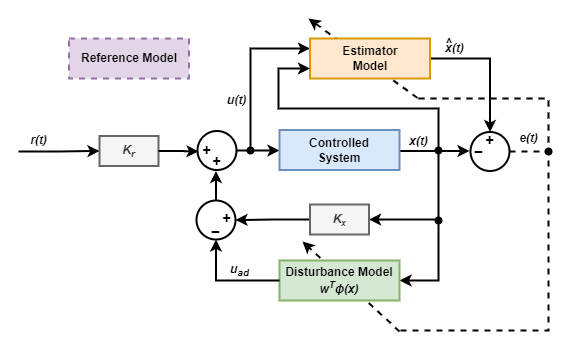
コントローラーは、制御入力 u(t) を次のように計算します。

$$\begin{array}{l}u\left(t\right)=k_{x}x\left(t\right)+k_{r}r\left(t\right)-u_{ad}\\ u_{ad}=w^T\varphi \left(x\right)\end{array}$$

ここで

• $$\widehat{x}$$(t) は推定器モデルで生成される制御対象システムの推定状態です。

• r(t) は外部基準信号です。

• k_x と k_r はフィードバック コントローラーとフィードフォワード コントローラーのゲインです。

• u_ad は外乱モデルから派生する適応制御コンポーネントです。

  ϕ(x) には外乱モデルの特徴が含まれます。

• w は適応外乱モデルの重みベクトルです。

コントローラーは、実際のシステムと推定されるシステムの状態の誤差 e(t) を計算します。その後、その誤差を使用して w の値をリアルタイムで適応させます。さらに、コントローラーは e(t) を使用して推定器モデルのパラメーターをリアルタイムで更新します。ゲイン k_x と k_r の値は、推定器モデルと参照モデルのパラメーターから派生します。

推定器モデルとコントローラーのゲイン

間接 MRAC コントローラーには、制御対象システムの推定器モデルとして以下が含まれています。

$$\dot{\widehat{x}}\left(t\right)=\widehat{A}x\left(t\right)+\widehat{B}u\left(t\right)$$

ここで

• $$\widehat{x}$$(t) は推定されるシステムの状態です。

• u(t) は制御入力です。

• $$\widehat{A}$$ は推定器の状態遷移行列です。

• $$\widehat{B}$$ は推定器の制御有効行列です。

コントローラーは、演算中に推定誤差 e(t) に基づいて $$\widehat{A}$$ と $$\widehat{B}$$ を更新します。

間接 MRAC コントローラーは、コントローラーのゲインを直接推定する代わりに、次のような動的な反転に基づく手法を使用して、参照モデルと推定器モデルのパラメーターからフィードバック ゲイン k_x とフィードフォワード ゲイン k_r を派生させます。

$$\begin{array}{l}{k}_r=\frac{B_m}{\widehat{B}}\\ k_x=\frac{1}{\widehat{B}}\left(A_m-\widehat{A}\right)\end{array}$$

ここで、$$\frac{1}{\widehat{B}}$$ は、行列 $$\widehat{B}$$ の Moore-Penrose 疑似逆行列です。

パラメーターの更新

間接 MRAC コントローラーは、次の方程式を使用して、状態ベクトル、放射基底関数、および外部ソースの特徴の定義のために推定器モデルのパラメーターと外乱モデルの重みを更新します [1] [2]。

$$\begin{array}{l}\dot{\widehat{A}}={\Gamma }_{a}x\left(t\right)e^T\left(t\right)P\\ \dot{\widehat{B}}={\Gamma }_{b}u\left(t\right)e^T\left(t\right)P\\ \dot{w}={\Gamma }_w\varphi \left(x\right)e^T\left(t\right)PB\end{array}$$

単一の隠れ層外乱モデルの更新方程式では、以下の更新方程式とともに同じ推定器モデルのパラメーターの更新を使用します。

$$\begin{array}{l}\dot{w}=-\left(\sigma \left(V^{T}x\right)-{\sigma }^{\prime }\left(V^{T}x\right)V^{T}x\right)e^T\left(t\right)PB{\Gamma }_w\\ \dot{V}=-{\Gamma }_{V}x{e}^T\left(t\right)PB{w}^T\sigma \left(V^{T}x\right)\end{array}$$

ここで、P は次のリアプノフ関数の解です。

$$k_{\tau }^{T}P+P{k}_{\tau }+Q=0$$

k_τ は推定器のフィードバック ゲインです。既定では、この値は参照モデルの状態遷移行列 A_m に対応します。ただし、推定器のフィードバック ゲインの別の値を指定できます。

学習修正

直接と間接のどちらの MRAC でも、学習率を高くしてロバスト性を高めるために、パラメーターの更新を変更してオプションのモーメンタム項を含めることができます。学習修正の方法には "シグマ修正" と "e-修正" の 2 つがあり、いずれかを選択できます。

シグマ修正の場合、それぞれのパラメーター更新のモーメンタム項は、運動量の重みパラメーター σ と現在のパラメーター値の積になります。たとえば、直接 MRAC コントローラー用の次の更新方程式にはシグマ修正項が含まれています。

$$\begin{array}{l}{\dot{k}}_x={\Gamma }_{x}x\left(t\right)e^T\left(t\right)PB+\sigma k_x\\ {\dot{k}}_r={\Gamma }_{r}r\left(t\right)e^T\left(t\right)PB+\sigma k_x\\ {\dot{w}}_x={\Gamma }_w\varphi \left(t\right)e^T\left(t\right)PB+\sigma w\end{array}$$

e-修正の場合、コントローラーはシグマ修正のモーメンタム項を誤差ベクトルのノルムでスケーリングします。たとえば、間接 MRAC コントローラー用の次の更新方程式には e-修正項が含まれています。

$$\begin{array}{l}\dot{\widehat{A}}={\Gamma }_{a}x\left(t\right)e^T\left(t\right)P+\sigma \left|e\left(t\right)\right|\widehat{A}\\ \dot{\widehat{B}}={\Gamma }_{b}u\left(t\right)e^T\left(t\right)P+\sigma \left|e\left(t\right)\right|\widehat{B}\\ {\dot{w}}_x={\Gamma }_w\varphi \left(t\right)e^T\left(t\right)PB+\sigma \left|e\left(t\right)\right|w\end{array}$$

いずれかの方法の学習修正の量を調整するには、運動量の重みパラメーター σ の値を変更します。

モデル規範形適応制御の詳細

モデル規範形適応制御の詳細については、ビデオをご覧ください。このビデオは、Learning-Based Control ビデオ シリーズの一部です。

参照

[1] Ioannou, Petros A., and Jing Sun. Robust Adaptive Control, Courier Corporation, 2012.

[2] Narendra, Kumpati S, and Anuradha M Annaswamy. Stable Adaptive Systems. Courier Corporation, 2012.

[3] Narendra, Kumpati S., and Anuradha M. Annaswamy. “Robust Adaptive Control.” In 1984 American Control Conference, 333–35. San Diego, CA, USA: IEEE, 1984. https://doi.org/10.23919/ACC.1984.4788398.

参考

ブロック

• Model Reference Adaptive Control

関連するトピック

• 衛星の回転のモデル規範形適応制御
• ウイング ロックが発生した航空機のモデル規範形適応制御