衛星の回転のモデル規範形適応制御
この例では、モデル規範形適応制御 (MRAC) を使用して不明な制御対象システムを理想の参照モデルに一致させることで衛星の回転を制御する方法を示します。衛星システムは Simulink® でモデル化され、MRAC コントローラーは Simulink Control Design™ ソフトウェアで提供される Model Reference Adaptive Control ブロックを使用して実装されます。
衛星回転の制御システム
この例のモデルでは、衛星の円柱形のボディがその対称軸 ("z" 軸) を中心として一定の角速度 で回転します [1]。目標は、 軸と 軸の角速度 と をトルク と を使用して別々に制御することです。運動方程式で 2 つの入力と 2 つの出力をもつ 2 次モデルを生成します。
このシステムでは、プラントの状態をコントローラーで直接は観測しません。代わりに、次の測定モデルを通じて間接的に状態を確認します。
この例では、実際のプラント モデルは不明であり、MRAC コントローラーでプラントのダイナミクスのノミナル モデルを使用すると仮定します。このノミナル モデルは次のとおりです。
この不確かさをもつ非線形システムについて、次の分離された参照モデルにシステムを追従させることができるコントローラーを設計することが目標になります。
ここで、以下となります。
は参照モデルの状態ベクトルです。
には角速度の基準信号が含まれます。
ノミナル モデルと参照モデルの定義
衛星システムの動的モデルを定義します。このシステムでは、A は実際の状態行列を表します。
a = 10; % System Constant A = [0 a;-a -a/2]; % True model parameters B = eye(2); C = [1 a;-a 1]; D = zeros(2,2);
プラントの不一致の行列を指定します。これは、コントローラーで使用されるノミナル プラントを定義するために実際の A 行列から差し引かれる行列です。このプラントの不確かさをモデル化することがコントローラーの目標になります。
deltaA = [0 0.5*a; -0.5*a 0]; % Plant mismatch参照システムは次の安定した 2 次システムです。
Am = [-5 0; 0 -5]; % Second-order decoupled integrator model Bm = diag([5 5]); % Nominal control effective matrix
衛星の回転速度と参照モデルの状態の初期条件を定義します。
x1_0 = 0.5; % Initial x-axis angular rate (rad/s) x2_0 = 0.5; % Initial y-axis angular rate (rad/s) xm_0 = [0;0]; % Initial conditions of the reference plant model
モデル規範形適応制御の構造
MRAC コントローラーの目標は、追従誤差 を漸近的に収束させることです。
MRAC コントローラーの構造は次のとおりです。
ここで、以下となります。
にはフィードバック制御ゲインが含まれます。
にはフィードフォワード制御ゲインが含まれます。
はモデルの不確かさを打ち消す適応制御項です。
Model Reference Adaptive Control ブロックは、目的の参照モデルの追従を実現するために適応制御項を調整します。オプションで、フィードバック制御とフィードフォワード制御のゲインを適応させることもできます。
この例では、コントローラーでフィードバック ゲインを適応させ、フィードフォワード ゲインは静的にします。
初期のフィードバック ゲインと静的なフィードフォワード ゲインは、次のモデル マッチング条件を満たすように計算されます。
計算されたコントローラーのゲインとフィードバック ゲインの学習率を指定します。
Kx = -place(A,B,eig(Am)); % State feedback gain for pole placement gain_kx = 1; % Feedback gain learning rate Kr = Bm; % Feedforward gain for ref model matching
不確かさの推定のパラメーターの構成
MRAC コントローラーは、モデルの不確かさをオンラインで推定し、不確かさを打ち消してベースライン コントローラーのノミナル システムを復元する適応制御動作 を生成します。システムの不確かさは、次のモデルを使用して適応制御項でモデル化されます。
ここで、以下となります。
にはコントローラーで調整されるネットワークの重みが含まれます。
は不確かさのモデルの特徴ベクトルです。
Model Reference Adaptive Control ブロックを使用して、次のいずれかの特徴ベクトル定義を選択できます。
システムの状態、
ガウス カーネルによる放射基底関数
オプションの入力端子で提供されるカスタム特徴。
この例では、外乱モデルの特徴としてシステムの状態を使用するようにコントローラーが構成されています。
モデル推定の学習率 gamma_w と追従誤差の重み Q を定義します。
gamma_w = 100; % Learning rate Q = 10; % Tracking error weight
コントローラーのシミュレーション
衛星回転の制御システムの Simulink モデルを開きます。
mdl = "satellitespin";
open_system(mdl)
モデルのシミュレーションを実行します。
Tf = 35; % Duration (s)
sim(mdl);回転の応答と回転速度の応答をそれぞれの基準信号と比較して、コントローラーの性能を確認します。
open_system(mdl + "/Scope1")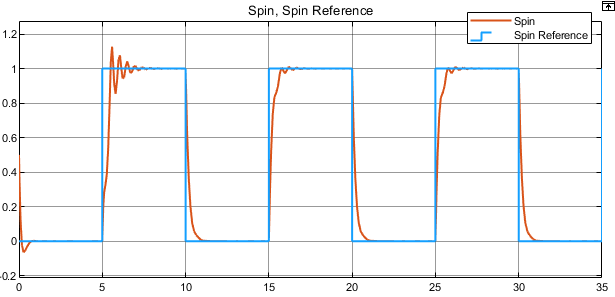
open_system(mdl + "/Scope3")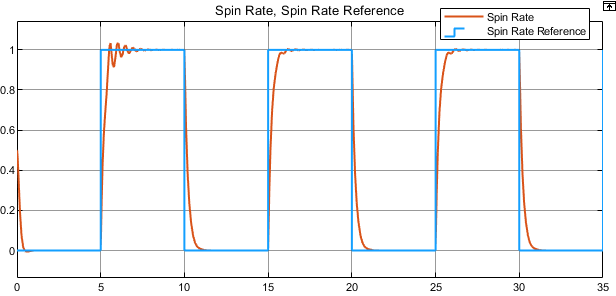
MRAC コントローラーは基準信号を適切に追従しています。最初のステップ応答に初期の過渡があり、コントローラーの外乱の推定が向上するにつれてサイズが小さくなっています。
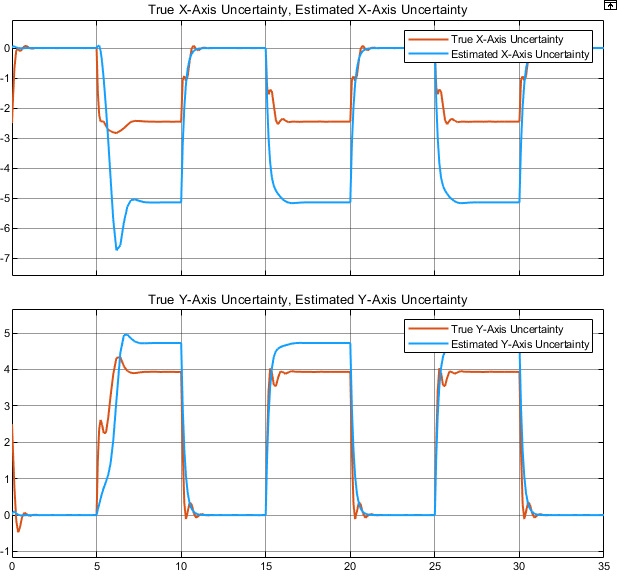
コントローラーで推定された不確かさを表示し、実際の不確かさと比較します。
open_system(mdl + "/Scope2")
コントローラーは "y" 軸の不確かさのモデルを正確に推定しています。"x" 軸の不確かさのモデルについては、符号は正しいものの、振幅が実際の不確かさよりも低くなっています。どちらの不確かさのモデルでも不確かさの推定に大きな過渡が見られ、特に基準信号の最初のステップ変化で大きくなっています。
推定される不確かさの応答の過渡を減らすために、追従誤差率 Q の値を小さくすることができます。たとえば、Q の値を 1 に減らしてモデルをシミュレートします。
Q = 1; sim(mdl);

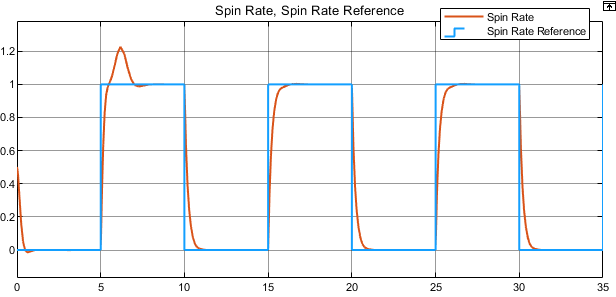
モデルの推定の応答で過渡が少なくなります。トレードオフとして、回転と回転速度の応答の整定時間が長くなっています。
参考文献
[1] Zhou, Kemin, John Comstock Doyle, and K. Glover. Robust and Optimal Control. Englewood Cliffs, N.J: Prentice Hall, 1996.