ソルバーの選択
動的システムをシミュレートするには、指定された時間範囲における連続タイム ステップのそれぞれの状態量を計算します。この計算では、システムのモデルにより提供された情報を使用します。"タイム ステップ" は、計算が生じる時間の間の隔たりです。この時間間隔のサイズを "ステップ サイズ" と呼びます。この方法でモデルの状態を計算するプロセスはモデルの "解決" として知られています。モデルを解く 1 つの方法がすべてのシステムに適用されるわけではありません。Simulink® には、"ソルバー" と呼ばれる一連のプログラムがあります。各ソルバーはモデルを解くための特定のアプローチを表します。
ソルバーは数値的手法によって、モデルを表す一連の常微分方程式を解きます。この計算により、ソルバーは次のシミュレーション ステップの時間を判断します。この初期値の問題を解決するプロセスにおいて、ソルバーは指定された精度要件も満たします。
動的システムの連続状態を表す常微分方程式 (ODE) を解くためのさまざまな数値積分技法が数学者によって開発されています。それぞれ特定の ODE 解法を実装する各種の固定ステップ連続ソルバーおよび可変ステップ連続ソルバー群が用意されています (ソルバーの比較を参照)。モデル コンフィギュレーション パラメーターの [ソルバー] ペインでソルバーを選択します。
MATLAB® および Simulink によって提供されているソルバーはすべて同じような命名規則に従います。つまり、ode の後ろに、ソルバーの次数を示す 2 つか 3 つの数字が付けられます。一部のソルバーはスティッフな微分方程式を解くことができ、そのソルバーによって使用されるメソッドは接尾辞 s、t、または tb で表されます。
ソルバーの自動選択
[ソルバー] パラメーターと [最大ステップ サイズ] パラメーターを [自動] に設定すると、ソフトウェアはアルゴリズムを使用してソルバーと最大ステップ サイズの値を選択します。ほとんどのモデルについては、ソフトウェアが、適切なソルバーとステップ サイズを選択できます。
アルゴリズムはいくつかのヒューリスティックな方法を使用して、モデルの特性に基づいてソルバーを選択します。このチャートは、選択アルゴリズムのヒューリスティックな方法をいくつか示しています。
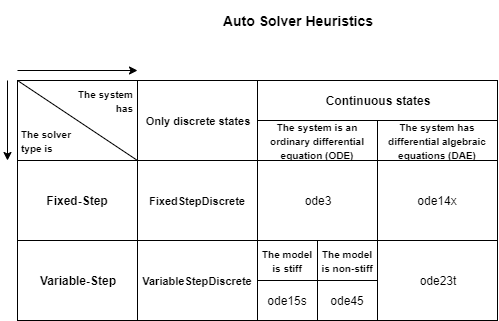
モデルに離散状態のみが含まれる場合、指定されたソルバー タイプの離散ソルバーが選択されます。
固定ステップ ソルバーについては、離散固定ステップ ソルバーが選択されます。
可変ステップ ソルバーについては、離散可変ステップ ソルバーが選択されます。
モデルに連続状態が含まれる場合、ソルバーの選択はソルバー タイプとモデルの数学的表現に基づいて行われます。
ODE を使用して表現できるシステムの固定ステップ ソルバーについては、
ode3ソルバーが選択されます。微分代数方程式系 (DAE) として表現できるシステムのモデルの固定ステップ ソルバーについては、
ode14xソルバーが選択されます。ODE を使用して表現できるシステムの可変ステップ ソルバーについては、モデルのスティッフ性に基づいてソルバーが選択されます。
スティッフなモデルについては、
ode15sソルバーが選択されます。スティッフではないモデルについては、
ode45ソルバーが選択されます。
DAE を使用して表現できるシステムの可変ステップ ソルバーについては、
ode23tソルバーが選択されます。
連続状態の数が NumStatesForStiffnessChecking パラメーターの値を下回ると、ソフトウェアはモデルのスティッフ性を計算します。既定では、NumStatesForStiffnessChecking パラメーターの値は 1000 です。
モデル内の連続状態の数が NumStatesForStiffnessChecking パラメーターの値を超えると、ソフトウェアはスティッフ性を計算せずにモデルをスティッフであると見なし、ode15s ソルバーを選択します。
モデル内の連続状態の数が NumStatesForStiffnessChecking パラメーターの値を下回ると、ソフトウェアはシステムのスティッフ性を計算し、StiffnessThreshold パラメーターの値に基づいてソルバーを選択します。
計算されたスティッフ性が
StiffnessThresholdパラメーターの値を下回ると、ソフトウェアはモデルをスティッフでないと見なし、ode45ソルバーを選択します。計算されたスティッフ性が
StiffnessThresholdパラメーターの値を超えると、ソフトウェアはモデルをスティッフであると見なし、ode15sソルバーを選択します。
NumStatesForStiffnessChecking パラメーターと StiffnessThreshold パラメーターの既定値は 1000 です。関数 set_param を使用して、それぞれのパラメーターに異なる値を指定できます。
Simscape™ Electrical™ モデルについては、ode23tb ソルバーが選択されます。Simscape Electrical を使用してモデル化されたシステムには、回路ブレーカーやパワー エレクトロニクスなどの非線形回路コンポーネントが含まれることがあり、スティッフ ソルバーが必要となります。
ソルバーの選択基準
モデルのシミュレーションに適したソルバーは次の特性によって異なります。
システム ダイナミクス
解の安定性
計算速度
ソルバーのロバスト性
そのため、Simulink によって提供される数値ソルバーは、おおまかに 2 つのプロパティによって分類できます。
計算のステップ サイズのタイプ
固定ステップ ソルバーでは、その名が示すように、シミュレーションの開始から終了まで同じステップ サイズを使用してモデルを解きます。ステップのサイズは指定することもソルバーに選択させることもできます。一般に、ステップ サイズを小さくすると結果の精度が向上し、システムのシミュレーションに要する時間が長くなります。
可変ステップ ソルバーでは、シミュレーション中にステップ サイズが変化します。これらのソルバーは、モデルのシミュレーション中に特定のイベント (急激な状態の変化、ゼロクロッシング イベントなど) が発生したときに精度を上げるためにステップ サイズを減らします。また、モデルの状態がゆっくり変化する場合は、ステップ サイズを大きくして不要なステップの実行を避けます。ステップ サイズの計算は、各ステップで計算のオーバーヘッドに加えられます。ただし、ステップの総数を減らすことができ、それによって、ゼロクロッシング、急激に変化する状態、および追加の計算を必要とするその他のイベントをもつモデルについて、指定したレベルの精度を維持するために必要なシミュレーション時間を減らせます。
モデルの状態
連続ソルバーは、数値積分を使って前のタイム ステップにおける状態と状態導関数から、現在のタイム ステップにおけるモデルの連続状態量を計算します。連続ソルバーは、個々のブロックに基づいて各タイム ステップにおけるモデルの離散状態量の値を計算します。
離散ソルバーは主に純粋な離散モデルを解くために使用されます。モデルについて、すぐ次のシミュレーション タイム ステップのみを計算します。この計算の実行時には、モデルの各ブロックに基づいてそれぞれの離散状態量が更新されます。連続状態は計算されません。
反復的手法を使用して、要件に適したソルバーを選択します。複数のソルバーのシミュレーション結果を比較し、最小のトレードオフで最適なパフォーマンスを提供するソルバーを選択します。
以下の方法で、モデルに適したソルバーを選択します。
自動ソルバーを使用します。新しいモデルでは、ソルバーの選択が既定値で自動ソルバーに設定されています。自動ソルバーは、モデルに対して固定ステップまたは可変ステップのソルバーと最大ステップ サイズを推奨します。
自動ソルバーを使用したシミュレーション結果が満足のいかないものである場合は、モデル コンフィギュレーション パラメーターの [ソルバー] ペインでソルバーを選択します。
モデルをビルドしてシミュレートするとき、モデルのダイナミクスに基づいてソルバーのタイプを選択できます。可変ステップ ソルバーは、ばね質量ダンパー システムのダイナミクスのような、純粋な連続モデルにより適しています。インバーター電力システムなど複数のスイッチを含むモデルの場合、ソルバーのリセット数の問題で、可変ステップ ソルバーも固定ステップ ソルバーのように振る舞うことになるため、固定ステップ ソルバーが推奨されます。
メモ
モデルを生成されたコードとして展開する場合は、固定ステップ ソルバーのみ使用できます。シミュレーション中に可変ステップ ソルバーを選択すると、そのソルバーを使用して展開時に必要となる固定ステップ ソルバーに必要なステップ サイズを計算します。
次のチャートは、Simulink ライブラリにおけるソルバーの大まかな分類を示しています。

選択したソルバーをモデルに合わせるには、シミュレーション精度の確認と改善を参照してください。
理想的には、選択されたソルバーは以下のようになります。
モデルを正常に解く。
可変ステップ ソルバーの場合、指定された許容誤差の限度内で解法を示す。
適切な期間でモデルを解く。
これらすべての目的が単一のソルバーで満たされるとは限りません。選択する前に、さまざまなソルバーを使用してシミュレーションを試してください。
Simulink ライブラリには複数のソルバーがあり、それらすべてが代数ループのソルバーと連携できます。詳細については、代数ループ ソルバーの動作を参照してください。
| ソルバーのタイプ | 陽的/陰的 | 離散 | 連続 | 可変次数 |
|---|---|---|---|---|
| 固定ステップ | 陽的 | 該当なし | 陽的な固定ステップ連続ソルバー | 該当なし |
| 暗黙的 | 該当なし | 陰的な固定ステップ連続ソルバー | 該当なし | |
| 可変ステップ | 陽的 | Simulink の可変ステップ ソルバー | 陽的な可変ステップ連続ソルバー | 単一次数連続ソルバーと可変次数連続ソルバー |
| 暗黙的 | 陰的な可変ステップ連続ソルバー | 単一次数連続ソルバーと可変次数連続ソルバー |
モデル コンフィギュレーション パラメーターの [ソルバー] ペインで、Simulink ライブラリにおけるソルバーは 2 つの主要なタイプに分類されます。固定ステップ ソルバーと可変ステップ ソルバーを参照してください。
ソルバーを比較するその他の方法については、以下を参照してください。
