微分代数方程式のモデル化

Robertson 反応例の概要

Robertson [1] は、スティッフシステムの数値ソルバーをテストおよび比較する自己触媒化学反応システムを作成しました。システムの反応、速度定数 (k) および反応速度 (V) は、次のとおりです。

$\begin{matrix} A & \overset{k_{1}}{\to} & B & k_{1} = 0.04 & V_{1} = k_{1} [A] \\ B + B & \overset{k_{2}}{\to} & C + B & k_{2} = 3 \cdot 10^{7} & V_{2} = k_{2} [B] [B] \\ B + C & \overset{k_{3}}{\to} & A + C & k_{3} = 1 \cdot 10^{4} & V_{3} = k_{3} [B] [C] \end{matrix}$

反応速度間に大きな差があるため、数値ソルバーは微分方程式をスティッフであると認識します。スティッフな微分方程式の場合、ステップサイズをきわめて小さくしない限り、数値ソルバーによっては解が収束しない場合があります。ステップサイズがきわめて小さい場合、シミュレーション時間が容認できないほど長くなります。このような場合、スティッフな方程式を解くために設計された数値ソルバーを使う必要があります。

ODE 方程式と DAE 方程式からの Simulink モデル

ライブスクリプトを開く

この例では、次の 3 つのモデルを使用します。

ex_hb1ode — 常微分方程式 (ODE) からの Simulink モデル。
ex_hb1dae — 微分代数方程式 (DAE) からの Simulink モデル。
ex_h1bdae_acb — Algebraic Constraint ブロックを使用した DAE 方程式からの Simulink モデル。

これらのファイルにアクセスするには、ライブスクリプトを開きます。

ODE 方程式からの Simulink モデル

連立常微分方程式 (ODE) には、以下の特性があります。

すべての方程式は常微分方程式である。
各方程式は、通常 "時間" である 1 つの独立変数に対する従属変数の導関数である。
連立内の方程式の数は従属変数の数と等しくなる。

反応速度を使用して、化学種ごとに変化率を記述する一連の微分方程式を作成できます。3 つの種があるため、この数学モデルには異なる 3 つの微分方程式があります。

$\begin{array}{l} A^{'} = - 0.04 A + 1 \cdot 10^{4} B C \\ B^{'} = 0.04 A - 1 \cdot 10^{4} B C - 3 \cdot 10^{7} B^{2} \\ C^{'} = 3 \cdot 10^{7} B^{2} \end{array}$

初期条件: $A = 1$ 、 $B = 0$ および $C = 0$ 。

モデルの作成

モデルを作成するか、モデル ex_hb1ode を開きます。

モデルに 3 つの Integrator ブロックを追加します。入力に A'、B' および C' と、出力に A、B および C というラベルをそれぞれ付けます。
Sum ブロック、Product ブロック、Gain ブロックを追加して、各微分変数の解を求めます。たとえば、信号 C' をモデル化する場合は次のようにします。
1. Math Function ブロックを追加し、入力を信号 B に接続します。[関数] パラメーターを [square] に設定します。
2. Math Function ブロックからの出力を Gain ブロックに接続します。[ゲイン] パラメーターを 3e7 に設定します。
3. 続けて残りの微分方程式の項をモデルに追加します。
A の Integrator ブロックの [初期条件] パラメーターを 1 に設定し、A の初期条件をモデル化します。
Out ブロックを追加し、信号 A、B および C を MATLAB 変数 yout に保存します。

モデルのシミュレーション

sim コマンドを使用してモデルをシミュレーションするスクリプトを作成します。このスクリプトは、シミュレーション結果を MATLAB 変数 yout に保存します。シミュレーションには長い時間間隔があり、B は初期段階で非常に高速に変化するため、対数スケールに値をプロットすることにより、視覚的に結果を比較することができます。また、B の値は A および C と比べて小さいため、値をプロットする前に B を $1 \cdot 10^{4}$ で乗算します。

次のステートメントを MATLAB^® スクリプトに入力します。独自のモデルを作成する場合は、ex_hblode をモデルの名前と置き換えます。
```
sim('ex_hb1ode')
yout(:,2) = 1e4*yout(:,2);
figure;
semilogx(tout,yout);
xlabel('Time');
ylabel('Concentration');
title('Robertson Reactions Modeled with ODEs')
```
Simulink^® エディターから、[モデル化] タブで、[モデル設定] をクリックします。
— [ソルバー] ペインで、[終了時間] を 4e5、[ソルバー] を [ode15s (stiff/NDF)] に設定します。
— [データのインポート/エクスポート] ペインで、[時間] および [出力] チェックボックスをオンにします。
スクリプトを実行します。すべての A が C に変換されることを確認します。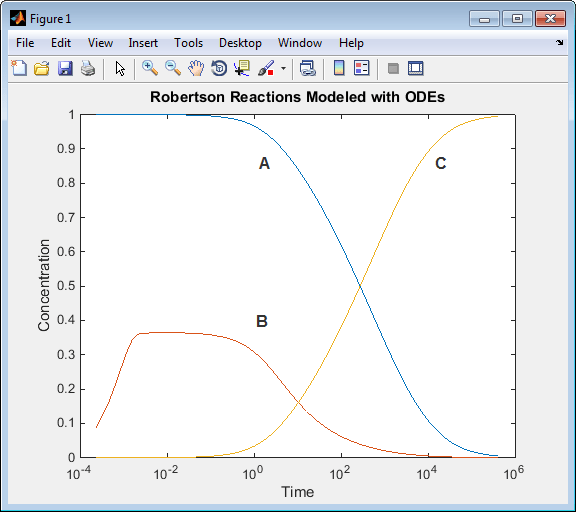

DAE 方程式からの Simulink モデル

連立微分代数方程式 (DAE) には以下の特性があります。

常微分方程式と代数方程式の両方が含まれる。代数方程式には導関数はない。
いくつかの方程式のみが一部の従属変数の導関数を定義する微分方程式である。その他の従属変数は代数方程式で定義される。
連立内の方程式の数は従属変数の数と等しくなる。

方程式系によっては質量やエネルギーの保存などの保存法則による制約があります。初期濃度を $A = 1$ 、 $B = 0$ および $C = 0$ に設定すると、 $A + B + C = 1$ であるため、3 つの種の総濃度は常に $1$ と等しくなります。 $C^{'}$ の微分方程式を次の代数方程式と置き換えることによって、一連の微分代数方程式 (DAE) を作成できます。

$C = 1 - A - B$

微分変数 A および B により代数変数 C が一意に決定します。

$\begin{array}{l} A^{'} = - 0.04 A + 1 \cdot 10^{4} B C \\ B^{'} = 0.04 A - 1 \cdot 10^{4} B C - 3 \cdot 10^{7} B^{2} \\ C = 1 - A - B \end{array}$

初期条件: $A = 1$ および $B = 0$ 。

モデルの作成

ご利用のモデルまたはモデル ex_hb1ode にこれらの変更を加えるか、モデル ex_hb1dae を開きます。

C を計算する Integrator ブロックを削除します。
Sum ブロックを追加し、[符号リスト] パラメーターを +– – に設定します。
信号 A と B を Sum ブロックのマイナス入力に接続します。
A の初期濃度を Sum ブロックのプラス入力に接続された Constant ブロックでモデル化します。[定数値] パラメーターを 1 に設定します。
Sum ブロックの出力を Product ブロックおよび Out ブロックに接続された分岐線に接続します。

モデルのシミュレーション

sim コマンドを使用してモデルをシミュレーションするスクリプトを作成します。

次のステートメントを MATLAB スクリプトに入力します。独自のモデルを作成する場合は、ex_hbldae をモデルの名前と置き換えます。
```
sim('ex_hb1dae')
yout(:,2) = 1e4*yout(:,2);
figure;
semilogx(tout,yout);
xlabel('Time');
ylabel('Concentration');
title('Robertson Reactions Modeled with DAEs')
```
Simulink エディターから、[モデル化] タブで、[モデル設定] をクリックします。
— [ソルバー] ペインで、[終了時間] を 4e5、[ソルバー] を [ode15s (stiff/NDF)] に設定します。
— [データのインポート/エクスポート] ペインで、[時間] および [出力] チェックボックスをオンにします。
スクリプトを実行します。代数方程式を使用したシミュレーションの結果は、微分方程式のみを使用したモデルのシミュレーションと同じです。

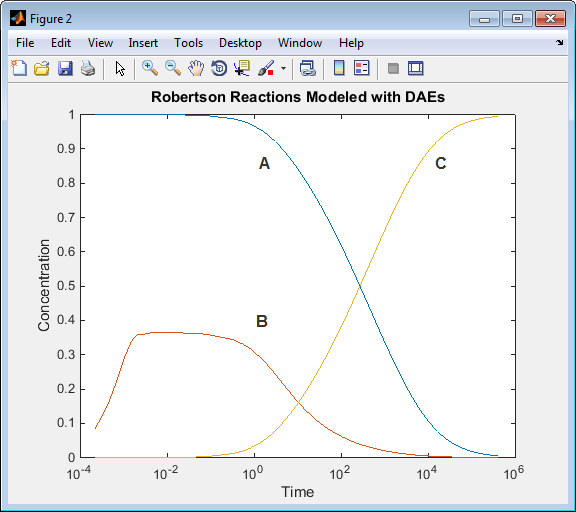
Algebraic Constraint ブロックを使用した DAE 方程式からの Simulink モデル

方程式系によっては質量やエネルギーの保存などの保存法則による制約があります。初期濃度を $A = 1$ 、 $B = 0$ および $C = 0$ に設定すると、 $A + B + C = 1$ であるため、3 つの種の総濃度は常に $1$ と等しくなります。

$C^{'}$ の微分方程式を Algebraic Constraint ブロックと Sum ブロックを使用してモデル化した代数方程式と置き換えることができます。Algebraic Constraint ブロックは、入力信号 F(z) をゼロに制限して、代数状態 z を出力します。言い換えれば、このブロック出力は、入力でゼロを生成するために必要な値です。ブロックに対する入力に次の代数方程式を使用します。

$0 = A + B + C - 1$

微分変数 A および B により代数変数 C が一意に決定します。

$\begin{array}{l} A^{'} = - 0.04 A + 1 \cdot 10^{4} B C \\ B^{'} = 0.04 A - 1 \cdot 10^{4} B C - 3 \cdot 10^{7} B^{2} \\ C = 1 - A - B \end{array}$

初期条件: $A = 1$ 、 $B = 0$ および $C = 1 \cdot 10^{- 3}$ 。

モデルの作成

ご利用のモデルまたはモデル ex_hb1ode にこれらの変更を加えるか、モデル ex_hb1dae_acb を開きます。

C を計算する Integrator ブロックを削除します。
Algebraic Constraint ブロックを追加します。[初期推定] パラメーターを 1e-3 に設定します。
Sum ブロックを追加します。[符号リスト] パラメーターを –+++ に設定します。
信号 A と B を Sum ブロックのプラス入力に接続します。
A の初期濃度を Sum ブロックのマイナス入力に接続された Constant ブロックでモデル化します。[定数値] パラメーターを 1 に設定します。
Algebraic Constraint ブロックの出力を、Product ブロック入力と Out ブロック入力の分岐線に接続します。
Algebraic Constraint ブロックの出力から Sum ブロックの最後のプラス入力に分岐線を作成します。

モデルのシミュレーション

sim コマンドを使用してモデルをシミュレーションするスクリプトを作成します。

次のステートメントを MATLAB スクリプトに入力します。独自のモデルを作成する場合は、ex_hbl_acb をモデルの名前と置き換えます。

sim('ex_hb1dae_acb')
yout(:,2) = 1e4*yout(:,2);
figure;
semilogx(tout,yout);
xlabel('Time');
ylabel('Concentration');
title('Robertson Reactions Modeled with DAEs and Algebraic Constraint Block')

Simulink エディターから、[モデル化] タブで、[モデル設定] をクリックします。
— [ソルバー] ペインで、[終了時間] を 4e5、[ソルバー] を [ode15s (stiff/NDF)] に設定します。
— [データのインポート/エクスポート] ペインで、[時間] および [出力] チェックボックスをオンにします。
スクリプトを実行します。Algebraic Constraint ブロックを使用したシミュレーションの結果は、微分方程式のみを使用したモデルのシミュレーションと同じです。

Algebraic Constraint ブロックを使用してモデル内に代数ループを作成します。[代数ループ] パラメーターを [警告] ([モデル化] タブで、[モデル設定] をクリックし、[診断] を選択) に設定すると、シミュレーション中に以下のメッセージが診断ビューアーに表示されます。

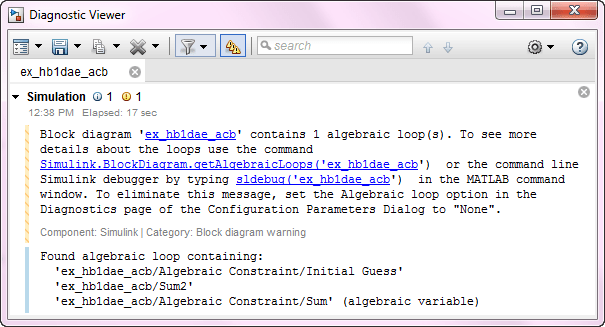
このモデルでは、代数ループソルバーでシミュレーションの解を求めることができましたが、代数ループが常に解をもつわけではありません。さらに、代数ループはコード生成でサポートされていません。Simulink モデル内の代数ループとその削除方法の詳細については、代数ループの概念を参照してください。

参照

[1] Robertson, H. H. “The solution of a set of reaction rate equations.” Numerical Analysis: An Introduction (J. Walsh ed.). London, England:Academic Press, 1966, pp. 178–182.