最適な形式の数学モデル
Series RLC の例
多くの場合、モデルを作成する数学システムはいくつかの方法で定式化できます。最適な形式の数学モデルを選択すると、高速でより正確にシミュレーションを実行できます。たとえば、次のような簡単な RLC 直列回路があるとします。
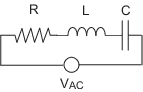
キルヒホフの電圧法則によると、この回路の電圧低下は、回路の各素子の電圧低下の合計と同じです。
オームの法則を使用して回路の各素子の電圧を解くと、この回路の方程式は次のように記述できます。
Simulink® では、抵抗電圧またはインダクタ電圧を解くことで、このシステムのモデルを作成できます。どちらを解くかによって、モデルの構造とそのパフォーマンスに影響します。
抵抗電圧を使用して Series RLC を解く
抵抗電圧に対して RLC 回路を解くと、次のようになります。
回路モデル
次のブロック線図は、Simulink でのモデルが作成されたこの方程式を示しています。ここで、R は 70、C は 0.00003、L は 0.04 です。抵抗電圧は、電圧源、コンデンサー電圧、およびインダクタ電圧の合計です。コンデンサー電圧とインダクタ電圧を計算するには、回路の電流が必要です。電流を計算するには、抵抗電圧に 1/R のゲインを乗算します。コンデンサー電圧は、電流を積分し、1/C のゲインを乗算して計算します。インダクタ電圧は、電流を微分し、L のゲインを乗算して計算します。
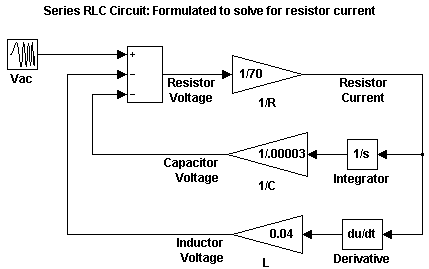
この定式化には、インダクタに関連付けられた Derivative ブロックが含まれています。Derivative ブロックを必要とする数学定式化は、システムが中断するため、できるだけ使用しないでください。時間はかかりますが、数値積分を使用して、モデルのダイナミクスを解きます。これらの積分ソルバーは、時間をかけて小さいステップを取り、解における精度の制約を満たします。Derivative ブロックによって発生した中断が大きすぎると、ソルバーでは解くことができません。
また、このモデルでは、Derivative ブロック、Sum ブロック、および 2 つの Gain ブロックが代数ループを作成します。代数ループは、モデルの実行速度を遅らせ、シミュレーション結果の精度を低下させる可能性があります。詳細については、代数ループの概念を参照してください。
インダクタ電圧を使用して Series RLC を解く
Derivative ブロックを使用しないようにするには、方程式を定式化し、インダクタ電圧に対して解きます。
回路モデル
次のブロック線図は、Simulink でモデルが作成された方程式を示しています。インダクタ電圧は、電圧源、抵抗電圧、およびコンデンサー電圧の合計です。抵抗電圧とコンデンサー電圧を計算するには、回路の電流が必要です。電流を計算するには、インダクタ電圧を積分し、L で除算します。コンデンサー電圧は、電流を積分し、C で除算して計算します。抵抗電圧は、電流を R の Gain で乗算して計算します。
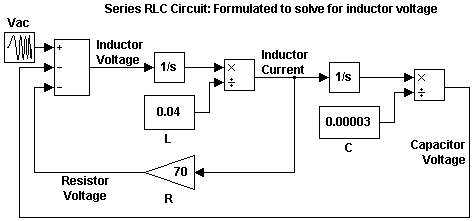
このモデルには、Integrator ブロックのみが含まれており、代数ループは含まれていません。その結果、モデルは、高速かつ正確にシミュレーションを行います。