Main Content

スピーカーの交差フィルター

ライブ スクリプトを開く

この例では、デジタル 3 ウェイ ラウドスピーカーの単純なモデルをどのように考案するかを説明します。システムは、オーディオ入力をウーファー、ミッドレンジ ドライバーおよびツィーターにそれぞれ対応する、低周波数帯域、中周波数帯域および高周波数帯域に分割します。帯域を区切る正規化交差周波数の標準値は、0.136π ラジアン/サンプルおよび 0.317π ラジアン/サンプルです。

ローパス、バンドパスおよびハイパス フィルターを作成し、低周波数、中周波数および高周波数の帯域を生成します。周波数を指定します。

lo = 0.136;
hi = 0.317;

各フィルターには 6 次のチェビシェフ I 型設計を使用します。実際のスピーカーの値より大きい 1 dB を通過帯域リップルに指定します。関数 cheby1 は、バンドパス設計の次数を 2 倍にします。バンドパス フィルターの次数を半分にして、すべてのフィルターの次数が同じになるようにします。各フィルターの零点、極およびゲインを返します。

ord = 6;
rip = 1;

[zw,pw,kw] = cheby1(ord,rip,lo);
[zm,pm,km] = cheby1(ord/2,rip,[lo hi]);
[zt,pt,kt] = cheby1(ord,rip,hi,'high');

フィルターの零点と極を可視化します。

zplane([zw zm zt],[pw pm pt])
lg = legend('Woofer','Midrange','Tweeter');
lg.Box = 'off';

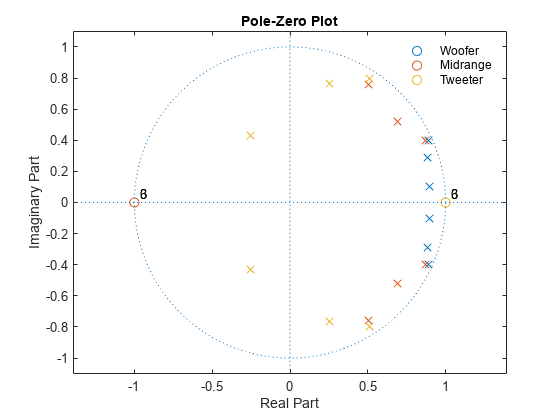
  • ウーファー: z=-1 の零点は、高周波数を抑制します。極は、0 と低位の交差周波数の間の振幅応答を強化します。

  • ミッドレンジ: z=0 と z=1 の零点は、高周波数と低周波数を抑制します。極は、低位と高位の交差周波数の間の振幅応答を強化します。

  • ツィーター: z=1 の零点は、低周波数を抑制します。極は、高位の交差周波数と π の間の振幅応答を強化します。

単位円上に振幅応答をプロットし、異なる極と零点の効果を確認します。線形ユニットを使用します。フィルターを 2 次セクションで表現します。

sw = zp2sos(zw,pw,kw);
sm = zp2sos(zm,pm,km);
st = zp2sos(zt,pt,kt);

nf = 1024;
[hw,fw] = freqz(sw,nf,'whole');
hm = freqz(sm,nf,'whole');
ht = freqz(st,nf,'whole');

plot3(cos(fw),sin(fw),[abs(hw) abs(hm) abs(ht)])
xlabel('Real')
ylabel('Imaginary')
view(75,30)
grid

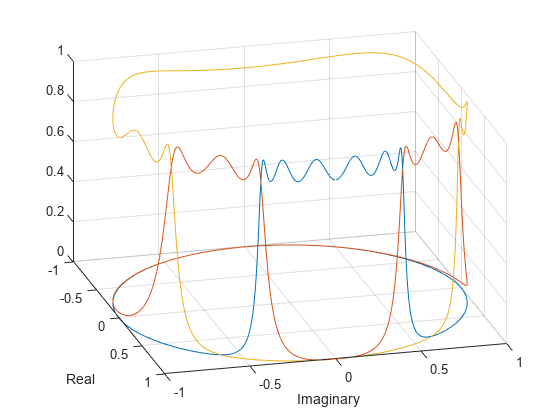
振幅応答を dB 単位でプロットします。

plot(fw/pi,mag2db(abs([hw hm ht])))
legend('Woofer','Mid-range','Tweeter')
xlabel('Normalized Frequency (\times\pi rad/sample)')
ylabel('Magnitude (dB)')
ylim([-60 0])

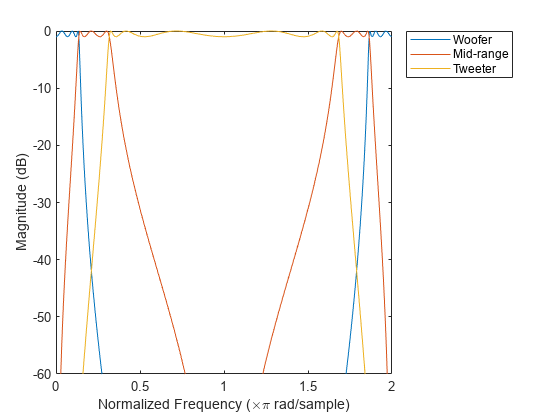
8192 Hz でサンプリングされたヘンデルの「ハレルヤ コーラス」の断章を含むオーディオ ファイルを読み込みます。フィルター処理によって、信号を 3 つの周波数帯域に分割します。帯域をプロットします。

load handel                % To hear, type soundsc(y,Fs)

yw = sosfilt(sw,y);        % To hear, type soundsc(yw,Fs)
ym = sosfilt(sm,y);        % To hear, type soundsc(ym,Fs)
yt = sosfilt(st,y);        % To hear, type soundsc(yt,Fs)

plot((0:length(y)-1)/Fs,[yw ym yt])
xlabel('Time (s)')

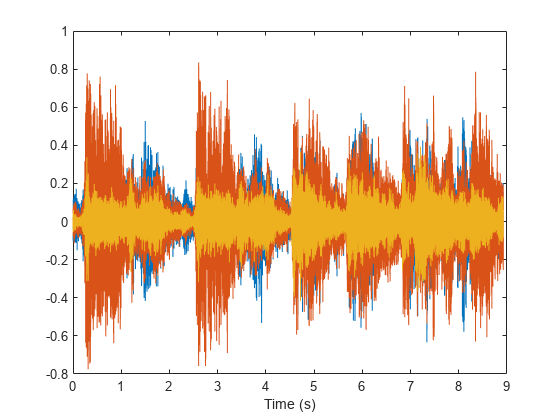
% To hear all the frequency ranges, type soundsc(yw+ym+yt,Fs)

参考文献

Orfanidis, Sophocles J. Introduction to Signal Processing. Englewood Cliffs, NJ: Prentice Hall, 1996.

参考

| | | |