生体信号からの分類特徴量の抽出

ライブスクリプトを開く

この例では、関数 midcross と関数 dtw を使用して、歩行信号データから特徴量を抽出する方法を説明します。歩行信号は、神経変性疾患をもつ患者の歩行パターンを調べるために使用されます。1 歩にかかる時間は、健常者と疾病患者で異なることが報告されています。midcross は、これらの時間を計算する際に便利です。また、人の歩行速度は時間とともに変化します。dtw は、歩行信号を時間に揃えて歪めることによって、信号形状の量的比較を扱いやすくします。この例では、midcross を使用して歩行信号内の各 1 歩の位置を特定し、dtw を使用して歩行信号のセグメント間の距離を計算します。これらの結果は、信号分類のための有力な特徴量として検証されます。この例では歩行信号のみを対象としていますが、これらの関数を使用して心電図 (ECG) や光電式容積脈波 (PPG) などの他の生体信号を解析することもできます。

1 歩にかかる時間間隔の測定

解析するデータセットには、筋萎縮性側索硬化症 (ALS) 患者と対照群を対象として歩行中に収集された力データが含まれます。ALS は、ルー・ゲーリッグ、スティーヴン・ホーキングおよび 2014 年の「アイスバケツチャレンジ」でよく知られるようになった疾患です。

1 人の患者を対象とした歩行信号データの最初の 30 秒間を読み込んでプロットします。

helperGaitPlot('als1m');
xlim([0 30])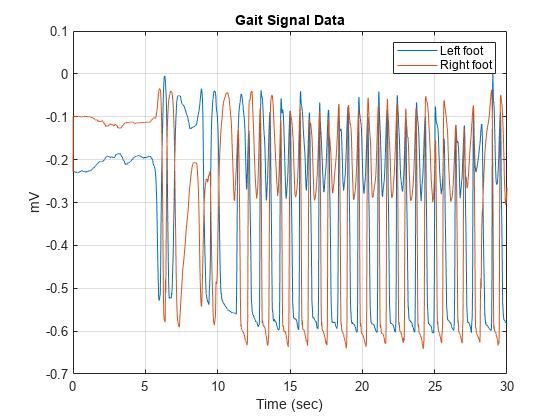

このデータセットは、足によって力感応抵抗器に与えられた力を表します。力はミリボルト単位で測定されています。各レコードの長さは 1 分間で、被験者の左足と右足に対応する個別のチャネルを含んでいます。データセット内の各 1 歩は、地面に足が着き、離れるときの力の急激な変化を特徴とします。midcross を使用し、ALS 患者を対象として、これらの急激な変化を特定します。

midcross を使用し、ALS 患者の左足を対象として、各クロッシングの位置を特定してプロットします。すべてのクロッシングが必ず検出されるように 25% の許容誤差を選択します。

Fs = 300;
gaitSignal = helperGaitImport('als1m');
midcross(gaitSignal(1,:),Fs,'tolerance',25);
xlim([0 30])
xlabel('Sample Number')
ylabel('mV')

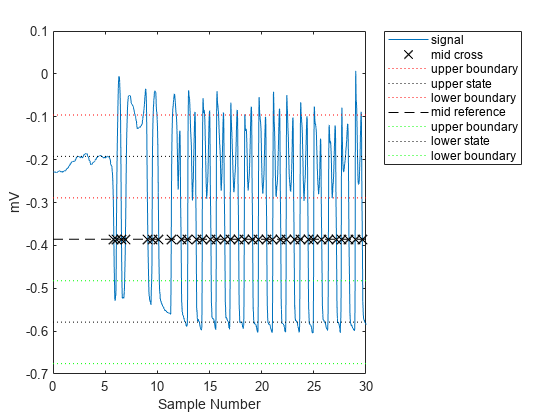
midcross は、クロッシングを正しく特定しています。今度は、これを使用し、10 人の患者のグループを対象に 1 歩にかかる時間を計算します。患者のうちの 5 人は対照被験者で、5 人は ALS に罹患しています。各患者の左足のレコードを使用し、過渡特性を除去するために最初の 8 つのクロッシングを除外します。

pnames = helperGaitImport();
for i = 1:10
  gaitSignal = helperGaitImport(pnames{i});
  IND2 = midcross(gaitSignal(1,:),Fs,'Tolerance',25);
  IST{i} = diff(IND2(9:2:end));   
  varIST(i) = var(IST{i});
end

1 歩にかかる時間をプロットします。

figure
hold on
for i = 1:5
  plot(1:length(IST{i}),IST{i},'.-r')
  plot(1:length(IST{i+5}),IST{i+5},'.-b')
end
xlabel('Stride Number')
ylabel('Time Between Strides (sec)')
legend('ALS','Control')

1 歩にかかる時間の分散は、ALS 患者の方が全体的に高くなっています。

歩行パターンの類似性の測定

各 1 歩間の距離を定量化したら、次に、これらの 1 歩間のばらつきに左右されない歩行信号データの形状を解析します。dtw を使用して、信号の 2 つのセグメントを比較します。治療または病気の進行に合わせて経時的に歩行信号の形状を比較するのが理想的です。ここでは、同じレコードの 2 つのセグメントを比較します。1 つは記録の初期に取得されたセグメント (sigsInitialLeft) で、もう 1 つは終わり近くのセグメント (sigsFinalLeft) です。各セグメントには、それぞれ 6 歩が含まれています。

歩行信号のデータセグメントを読み込みます。

load PNGaitSegments.mat

患者は、レコード全体を通して同じ速度で歩いているわけではありません。dtw は、これらを歪めて時間で揃えることでセグメント間の距離の測定を行います。dtw を使用して 2 つのセグメントを比較します。

figure
dtw(sigsInitialLeft{1},sigsFinalLeft{1});
legend('Early segment','Later segment','location','southeast')

2 つのセグメントが時間で揃えられています。元の信号のオフセットでわかるように、患者の歩行速度は時間とともに変化しているようですが、dtw は、どちらか一方のセグメントのサンプルを重複させることで 2 つのセグメントを一致させます。dtw を使用して得られた距離は、1 歩にかかる時間の分散とともに、歩行信号分類器用の特徴量として調査されます。

信号分類のための特徴ベクトルの作成

歩行信号に基づいて患者が健康かどうかを判断するための分類器を作成しているとします。1 歩にかかる時間の分散 feature1 と、dtw で得た最初と最後の信号セグメント間の距離 feature2 を分類特徴量として調べます。

feature1 は、先に midcross を使用して計算されています。

feature1 = varIST;

ALS 患者と対照群の feature2 を抽出します。

feature2 = zeros(10,1);
for i = 1:length(sigsInitialLeft)
  feature2(i) = dtw(sigsInitialLeft{i},sigsFinalLeft{i});
end

ALS の被験者と対照被験者の特徴量をプロットします。

figure
plot(feature1(1:5),feature2(1:5),'r*',...
    feature1(6:10),feature2(6:10),'b+',...
    'MarkerSize',10,'LineWidth',1)
xlabel('Variance of Inter-Stride Times')
ylabel('Distance Between Segments')
legend('ALS','Control')

ALS 患者の場合、1 歩にかかる時間の分散はより大きいですが、dtw で得たセグメント間の距離はより小さくなるようです。これらの特徴量は、相互補完的であり、調査してニューラルネットワークやサポートベクターマシンなどの分類器で使用することができます。

まとめ

midcross および dtw では、動作や行為の速度がさまざまであるため時間につれて不規則に繰り返される、歩行信号やその他の生体データを簡便に比較できます。この例では、midcross を使用して各 1 歩の時間の位置を特定し、dtw を使用してセグメントの距離を計算しました。midcross の距離が測定する時間のばらつきを dtw が排除したため、これらは相補的な方法でした。特徴量として、これら 2 つの計量は、このデータセットの対照患者と ALS 患者の間の区別を示しました。midcross および dtw は、同様に、活動の関数として形状が変化する他の生体信号を調べるために使用できました。

参考文献

[1] Goldberger, A. L., L. A. N. Amaral, L. Glass, J. M. Hausdorff, P. Ch. Ivanov, R. G. Mark, R. G. Mietus, G. B. Moody, C.-K. Peng, and H. E. Stanley. "PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals." Circulation. Vol. 101, Number 23, 2000, pp. e215-e200.

参考

dtw | midcross