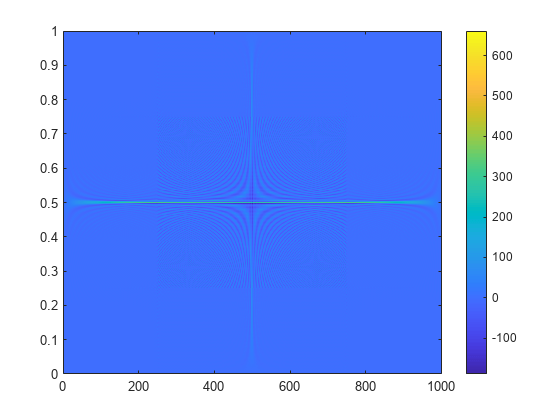
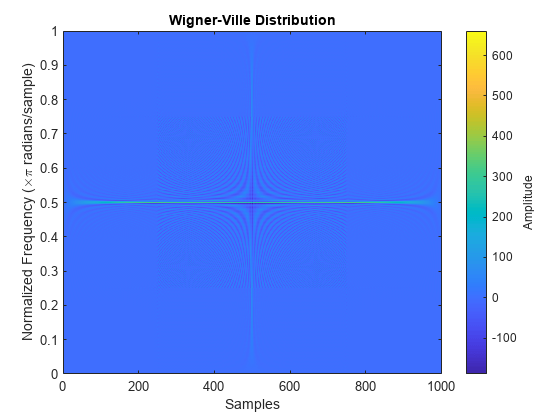
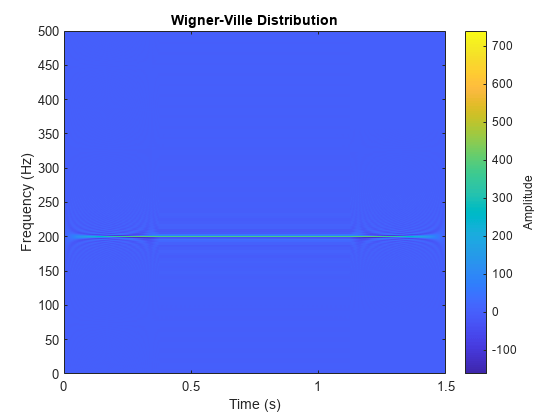
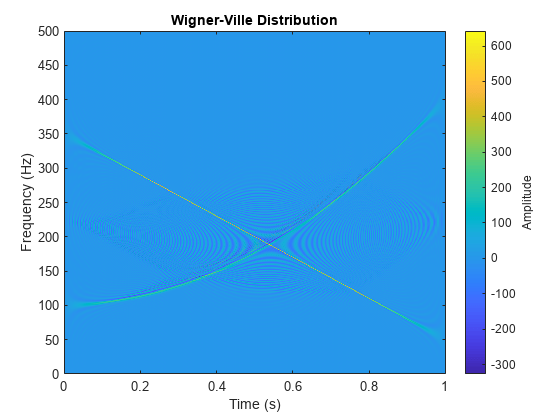
wvd

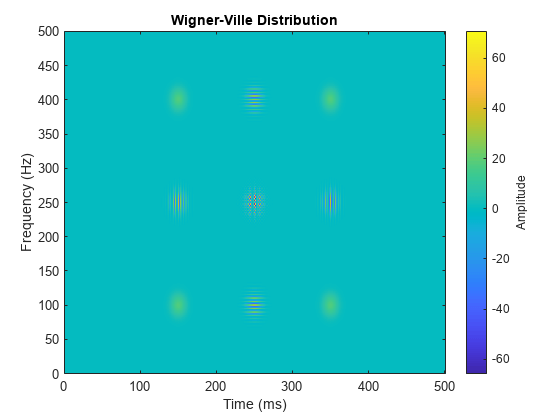
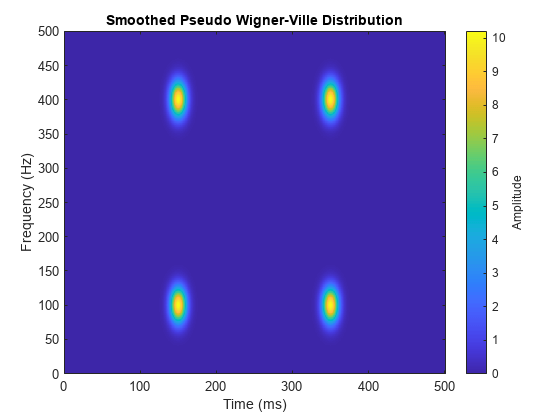
Wigner-Ville 分布と平滑化疑似 Wigner-Ville 分布

構文

d = wvd(x)

d = wvd(x,fs)

d = wvd(x,ts)

d = wvd(___,"smoothedPseudo")

d = wvd(___,"smoothedPseudo",twin,fwin)

d = wvd(___,"smoothedPseudo",Name=Value)

d = wvd(___,MinThreshold=thresh)

[d,f,t] = wvd(___)

wvd(___)

説明

d = wvd(x) は、x の Wigner-Ville 分布を返します。

d = wvd(x,fs) は、x がレート fs でサンプリングされたときの Wigner-Ville 分布を返します。

d = wvd(x,ts) は、x がサンプル間の時間間隔 ts でサンプリングされたときの Wigner-Ville 分布を返します。

d = wvd(___,"smoothedPseudo") は、x の平滑化疑似 Wigner-Ville 分布を返します。この関数は、入力信号の長さを使用して、時間と周波数の平滑化に使用されるウィンドウの長さを選択します。この構文には、前の構文の入力引数を任意に組み合わせて含めることができます。

d = wvd(___,"smoothedPseudo",twin,fwin) は、平滑化に使用される時間ウィンドウ twin と周波数ウィンドウ fwin を指定します。時間または周波数の平滑化に既定のウィンドウを使用するには、対応する引数を空 ([]) に指定します。

d = wvd(___,"smoothedPseudo",Name=Value) は、名前と値の引数を使用して、平滑化疑似 Wigner-Ville 分布の追加オプションを指定します。この構文では、twin と fwin を指定できます。また、省略することもできます。

d = wvd(___,MinThreshold=thresh) は、振幅が thresh より小さい d の要素をゼロに設定します。この構文は、Wigner-Ville 分布と平滑化疑似 Wigner-Ville 分布の両方に適用されます。

[d,f,t] = wvd(___) は、周波数のベクトル f と、d が計算される時間のベクトル t も返します。

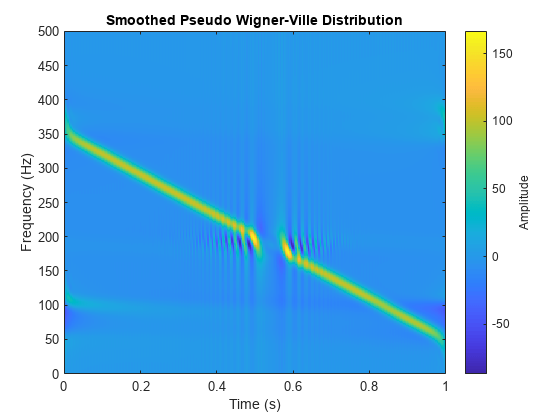
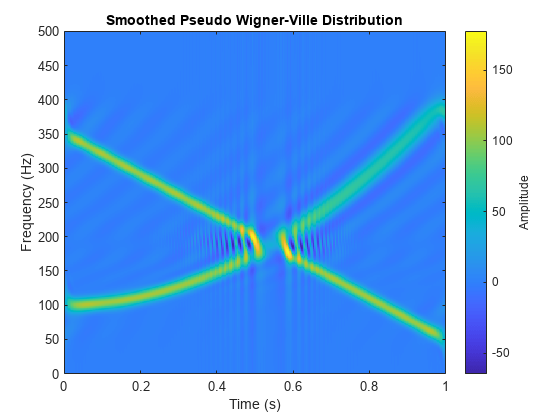
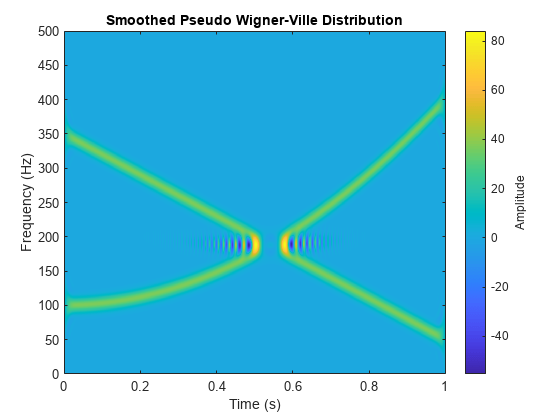
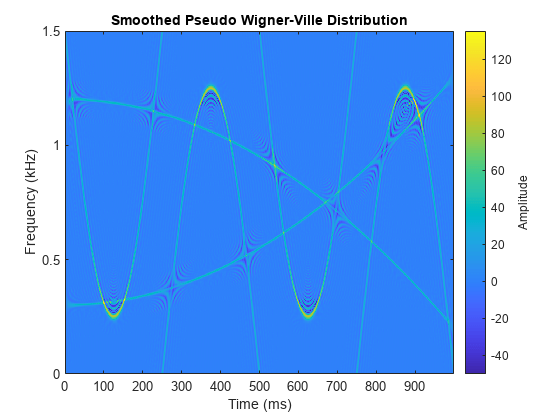
出力引数なしで wvd(___) を使用すると、現在の Figure に Wigner-Ville 分布または平滑化疑似 Wigner-Ville 分布がプロットされます。

例

インパルスとトーンの Wigner-Ville 分布

$\pi /2$ の正規化周波数を持つ、1000 サンプル インパルスと 1000 サンプル トーンを生成します。2 つの信号の和の Wigner-Ville 分布を計算します。

x = zeros(1001,1);
x(500) = 10;

y = sin(pi*(0:1000)/2)';

[d,f,t] = wvd(x+y);

Wigner-Ville 分布をプロットします。

imagesc(t,f,d)
axis xy
colorbar

出力引数なしで wvd を呼び出して結果を再現します。

wvd(x+y)

正弦波の Wigner-Ville 分布

1 kHz で 1.5 秒間サンプリングされた 200 Hz の正弦波で構成される信号を生成します。

fs = 1000;
t = (0:1/fs:1.5)';
x = cos(2*pi*t*200);

信号の Wigner-Ville 分布を計算します。

wvd(x,fs)

250 Hz と 450 Hz の間で周波数が正弦関数的に変化するチャープを信号に追加します。信号を MATLAB® の timetable に変換します。Wigner-Ville 分布を計算します。

x = x + vco(cos(2*pi*t),[250 450],fs);
xt = timetable(seconds(t),x);

wvd(xt)

振幅が 0 より小さい分布要素をゼロに設定します。

wvd(xt,MinThreshold=0)

チャープの Wigner-Ville 分布

1 kHz で 1 秒間サンプリングされた信号を生成します。信号の 1 つの成分は、測定中に周波数が 100 Hz から 400 Hz に 2 次的に増加するチャープです。信号のもう 1 つの成分は、同じ時間で周波数が 350 Hz から 50 Hz に線形的に減少するチャープです。

信号を timetable に保存します。

fs = 1000;
t = 0:1/fs:1;

x = chirp(t,100,1,400,"quadratic") + chirp(t,350,1,50);

信号の Wigner-Ville 分布を計算します。

wvd(x,fs)

信号の平滑化疑似 Wigner-Ville 分布を計算します。501 個の周波数点と 502 個の時間点を指定します。

wvd(x,fs,"smoothedPseudo",NumFrequencyPoints=501,NumTimePoints=502)

時間点の数を増やして、2 次チャープが表示されるようにします。

wvd(x,fs,"smoothedPseudo",NumFrequencyPoints=501,NumTimePoints=522)

シャープなイメージを得るために、周波数点と時間点を増やします。

wvd(x,fs,"smoothedPseudo",NumFrequencyPoints=1000,NumTimePoints=1502)

複素信号の平滑化疑似 Wigner-Ville 分布

3 kHz で 1 秒間サンプリングされた 2 成分信号を生成します。最初の成分は 2 次チャープで、測定中に周波数が 300 Hz から 1300 Hz に増加します。2 番目の成分は、正弦関数的に変化する周波数成分を持つチャープです。信号はホワイト ガウス ノイズに組み込まれます。連続するサンプル間の時間を duration スカラーとして表します。

fs = 3000;
t = 0:1/fs:1-1/fs;
dt = seconds(t(2)-t(1));

x1 = chirp(t,300,t(end),1300,"quadratic");
x2 = exp(2j*pi*100*cos(2*pi*2*t));

x = x1 + x2 + randn(size(t))/10;

信号の平滑化疑似 Wigner-Ville を計算してプロットします。601 サンプルのハミング ウィンドウを使用して時間領域で、305 サンプルの箱型ウィンドウを使用して周波数領域で、それぞれ分布にウィンドウを適用します。表示用に 600 個の周波数点を使用します。振幅が $-$50 より小さい分布の成分をゼロに設定します。

wvd(x,dt,"smoothedPseudo",hamming(601),rectwin(305), ...
    NumFrequencyPoints=600,MinThreshold=-50)

干渉項

4 つのガウス原子で構成された信号を生成します。各原子は、ガウスにより変調された正弦波で構成されています。正弦波には 100 Hz と 400 Hz の周波数があります。ガウスの中心は 150 ミリ秒と 350 ミリ秒で、$0.{01}^2$ の分散があります。すべての原子に単位振幅があります。信号は、1 kHz で 0.5 秒間サンプリングされます。

fs = 1000;
t = (0:1/fs:0.5)';

f1 = 100;
f2 = 400;

mu1 = 0.15;
mu2 = 0.35;

gaussFun = @(A,x,mu,f) exp(-(x-mu).^2/(2*0.01^2)).*sin(2*pi*f.*x)*A';

s = gaussFun([1 1 1 1],t,[mu1 mu1 mu2 mu2],[f1 f2 f1 f2]);

信号の Wigner-Ville 分布を計算して表示します。負の値を持つ可能性がある干渉項が、自動項の各ペアの中間に表示されます。

wvd(s,fs)

信号の平滑化疑似 Wigner-Ville 分布を計算して表示します。時間と周波数の平滑化により干渉項が減衰されます。

wvd(s,fs,"smoothedPseudo")

入力引数

x — 入力信号

ベクトル | timetable

入力信号。ベクトルまたは単一のベクトル変数を含む MATLAB^® の timetable として指定します。

• x が timetable の場合、増加する有限の行時間を含んでいなければなりません。

• timetable が欠損している場合や時間点が重複している場合、欠損または重複する時間および非等間隔の時間をもつ timetable の整理のヒントを使用して修正できます。

入力信号の長さが奇数の場合は、関数によりゼロが追加され、長さが偶数になります。

例: cos(pi/8*(0:159))'+randn(160,1)/10 は、ホワイト ノイズに含まれる正弦波を指定します。

例: timetable(seconds(0:5)',rand(6,1)) は 1 Hz で 5 秒間サンプリングされた確率変数を指定します。

データ型: single | double
複素数のサポート: あり

fs — サンプル レート

2*pi (既定値) | 正の数値スカラー

サンプル レート。正の数値スカラーとして指定します。

ts — サンプル時間

duration スカラー

サンプル時間。duration スカラーで指定します。

twin, fwin — 時間ウィンドウと周波数ウィンドウ

長さが奇数のベクトル

平滑化に使用される時間ウィンドウと周波数ウィンドウ。長さが奇数のベクトルとして指定します。既定では、wvd は形状係数β = 20 のカイザー ウィンドウを使用します。

• twin の既定の長さは、round(length(x)/10) 以上の最も小さい奇数の整数です。

• fwin の既定の長さは、nf/4 以上の最も小さい奇数の整数です。nf は NumFrequencyPoints を使用して指定します。

各ウィンドウの長さは、2*ceil(length(x)/2) 以下でなければなりません。

例: kaiser(65,0.5) は、0.5 の形状係数を持つ 65 サンプルのカイザー ウィンドウを指定します。

thresh — 最小非ゼロ値

-Inf (既定値) | 実数スカラー

最小非ゼロ値。実数スカラーとして指定します。関数は、振幅が thresh より小さい d の要素をゼロに設定します。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、コンマを使用して名前と値をそれぞれ区切り、Name を引用符で囲みます。

例: 'NumFrequencyPoints',201,'NumTimePoints',300 は、201 個の周波数点と 300 個の時間点における Wigner-Ville 分布を計算します。

NumFrequencyPoints — 周波数点の数

2*ceil(length(x)/2) (既定値) | 整数

周波数点の数。整数として指定します。この引数は、周波数のオーバーサンプリングの程度を制御します。周波数点の数は、(length(fwin)+1)/2 以上でなければならず、既定よりも大きくすることはできません。

NumTimePoints — 時間点の数

4*ceil(length(x)/2) (既定値) | 偶数の整数

時間点の数。偶数の整数として指定します。この引数は、時間のオーバーサンプリングの程度を制御します[3]。時間点の数は、2*length(twin) 以上でなければならず、既定よりも大きくすることはできません。

ヒント

入力信号が大きい場合、メモリ要求を下げて計算速度を上げるために時間点の数を減らします。

出力引数

d — Wigner-Ville 分布

行列

Wigner-Ville 分布。行列として返されます。時間は d の列方向に、周波数は行方向に下がって増加します。行列のサイズは N_f × N_t です。ここで、N_f は f の長さ、N_t は t の長さです。

f — 周波数

ベクトル

ベクトルとして返される周波数。

• 入力に時間情報がある場合、f は Hz 単位で表される周波数を含みます。

• 入力に時間情報がない場合、f はラジアン/サンプル単位で表される正規化周波数を含みます。

t — 時点

ベクトル

時点。ベクトルとして返されます。

• 入力に時間情報がある場合、t は秒単位で表される時間値を含みます。

• 入力に時間情報がない場合、t はサンプル数を含みます。

詳細

Wigner-Ville 分布

"Wigner-Ville 分布" は、信号の高分解能な時間-周波数表現を提供します。この分布は、信号の可視化、検出、および推定に応用されます。

連続信号 x(t) では、Wigner-Ville 分布は次のように定義されます。

$${\text{WVD}}_x(t,f)={\displaystyle {\int }_{-\infty }^{\infty }x\left(t+\frac{\tau }{2}\right)x^{*}\left(t-\frac{\tau }{2}\right)e^{-j2\pi f\tau }d\tau .}$$

N 個のサンプルを持つ離散信号では、分布は次のようになります。

$${\text{WVD}}_x(n,k)={\displaystyle \sum _{m=-N}^{N}x(n+m/2)x^{*}(n-m/2)e^{-j2\pi km/N}}.$$

奇数値の m では、この定義は半整数サンプル値での信号の評価を必要とします。これにより内挿が必要となるため、エイリアシングを避けるために離散フーリエ変換をゼロ パディングする必要があります。

Wigner-Ville 分布には、その解釈を複雑にしがちな干渉項が含まれています。分布をシャープにするために、ローパス ウィンドウで定義をフィルター処理できます。平滑化疑似 Wigner-Ville 分布は、時間と周波数の平滑化に個別のウィンドウを使用します。

$${\text{SPWVD}}_x^{g,H}(t,f)={\displaystyle {\int }_{-\infty }^{\infty }g(t)H(f)x\left(t+\frac{\tau }{2}\right)x^{*}\left(t-\frac{\tau }{2}\right)e^{-j2\pi f\tau }d\tau .}$$

参照

[1] Cohen, Leon. Time-Frequency Analysis: Theory and Applications. Englewood Cliffs, NJ: Prentice-Hall, 1995.

[2] Mallat, Stéphane. A Wavelet Tour of Signal Processing. Second Edition. San Diego, CA: Academic Press, 1999.

[3] O'Toole, John M., and Boualem Boashash. "Fast and Memory-Efficient algorithms for Computing Quadratic Time-Frequency Distributions." Applied and Computational Harmonic Analysis. Vol. 35, Number 2, 2013, pp. 350–358.

拡張機能

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

GPU コード生成
GPU Coder™ を使用して NVIDIA® GPU のための CUDA® コードを生成します。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

この関数は、GPU 配列を完全にサポートします。詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2018b で導入

R2023b: wvd は GPU コード生成をサポートする

関数 wvd は、NVIDIA^® GPU 用の CUDA^® コード生成をサポートします。CUDA コードを生成するには、MATLAB Coder™ および GPU Coder™ が必要です。

R2023a: コード生成向けの timetable のサポート

関数 wvd は、コード生成向けに timetable 入力をサポートします。

参考

関数

• fsst | pspectrum | spectrogram | xwvd

トピック

• 時間-周波数ギャラリー