rainflow
疲労解析のためのレインフロー カウント
構文
説明
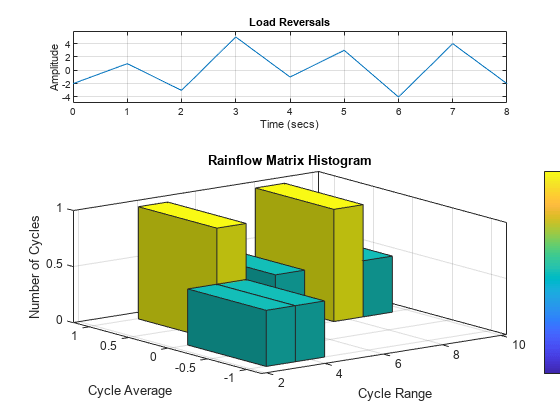
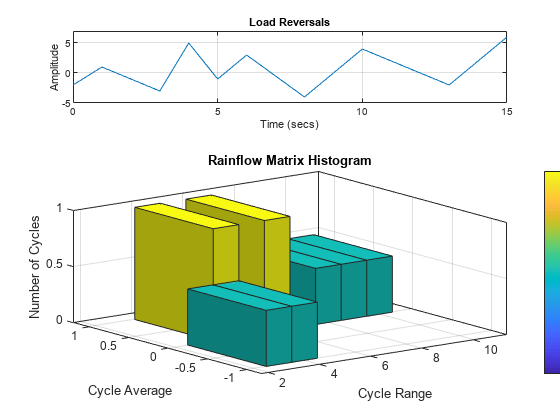
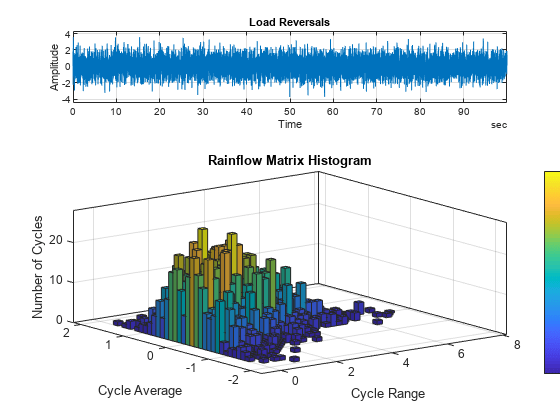
出力引数を設定せずに rainflow(___) を使用すると、現在の Figure に負荷の反転とレインフロー行列ヒストグラムがプロットされます。
例
入力引数
出力引数
アルゴリズム
疲労解析では、応力が周期的に変化する状況下で、対象物にどのように損傷が蓄積されるかを調べます。対象物の破損に必要なサイクル数は、サイクルの振幅によって異なります。広帯域入力励起にはさまざまな振幅のサイクルが含まれ、対象物内のヒステリシスの影響によって一部のサイクルが他のサイクルに完全または部分的にネストされます。"レインフロー計数" は、負荷の変化サイクルの数をサイクル振幅の関数として推定します。
rainflow は、はじめに負荷履歴を "反転" のシーケンスにします。反転は、負荷が符号を変化させる局所的最小値と局所的最大値です。関数は、シーケンスの基準点 Z の移動と、これらの特性をもつ順序付けられた 3 点のサブセットの移動を考慮してサイクルをカウントします。
最初の点と 2 番目の点を、まとめて Y とします。
2 番目の点と 3 番目の点を、まとめて X とします。
X と Y の両方で、点は早いものから遅いものへと時間順に並べ替えられますが、必ずしも反転シーケンス内で連続しているわけではありません。
r(X) によって表される X の "範囲" は、最初の点の振幅と 2 番目の点の振幅の間の差の絶対値です。r(Y) の定義も同様です。
rainflow アルゴリズムは、以下のように実行されます。
最後に、関数はさまざまなサイクルと半サイクルを収集し、その範囲、平均、開始点、終了点を集計します。これらの情報は、後で、サイクルのヒストグラムの作成に使用できます。
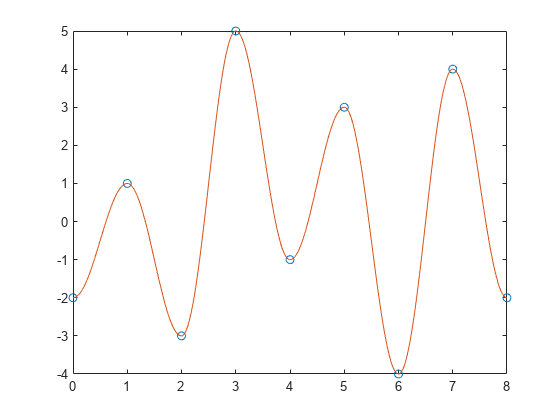
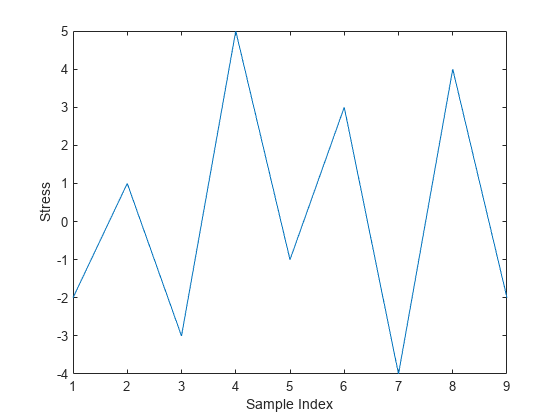
次の反転シーケンスについて考えます。
| 手順 | Z | 反転 | 3 つの反転の有無 | Y | r(Y) | X | r(X) | r(X) < r(Y)? | Z in Y? | アクション |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | A | A, B, C | あり | AB | 3 | BC | 4 | なし | あり |
|
| 2 | B | B, C | なし | — | — | — | — | — | — | D を読み取る |
| 3 | B | B, C, D | あり | BC | 4 | CD | 8 | なし | あり |
|
| 4 | C | C, D | なし | — | — | — | — | — | — | E を読み取る |
| 5 | C | C, D, E | あり | CD | 8 | DE | 6 | あり | — | F を読み取る |
| 6 | C | C, D, E, F | あり | DE | 6 | EF | 4 | あり | — | G を読み取る |
| 7 | C | C, D, E, F, G | あり | EF | 4 | FG | 7 | なし | なし |
|
| 8 | C | C, D, G | あり | CD | 8 | DG | 9 | なし | あり |
|
| 9 | D | D, G | なし | — | — | — | — | — | — | H を読み取る |
| 10 | D | D, G, H | あり | DG | 9 | GH | 8 | あり | — | J を読み取る |
| 11 | D | D, G, H, J | あり | GH | 8 | HJ | 7 | あり | — | K を読み取る |
| 12 | D | D, G, H, J, K | あり | HJ | 7 | JK | 4 | あり | — | L を読み取る |
| 13 | D | D, G, H, J, K, L | あり | JK | 4 | KL | 3 | あり | — | M を読み取る |
| 14 | D | D, G, H, J, K, L, M | あり | KL | 3 | LM | 5 | なし | なし |
|
| 15 | D | D, G, H, J, M | あり | HJ | 7 | JM | 5 | あり | — | N を読み取る |
| 16 | D | D, G, H, J, M, N | あり | JM | 5 | MN | 1 | あり | — | P を読み取る |
| 17 | D | D, G, H, J, M, N, P | あり | MN | 1 | NP | 4 | なし | なし |
|
| 18 | D | D, G, H, J, P | あり | HJ | 7 | JP | 9 | なし | なし |
|
| 19 | D | D, G, P | あり | DG | 9 | GP | 10 | なし | あり |
|
| 20 | G | G, P | データ範囲外 | — | — | — | — | — | — | GP を ½ サイクルとしてカウント |
ここで結果を収集します。
| サイクル カウント | 範囲 | 平均 | 開始 | 終了 |
|---|---|---|---|---|
| ½ | 3 | –0.5 | A | B |
| ½ | 4 | –1 | B | C |
| 1 | 4 | 1 | E | F |
| ½ | 8 | 1 | C | D |
| 1 | 3 | –0.5 | K | L |
| 1 | 1 | 2.5 | M | N |
| 1 | 7 | 0.5 | H | J |
| ½ | 9 | 0.5 | D | G |
| ½ | 10 | 1 | G | P |
これをシーケンスで rainflow を実行した結果と比較します。
q = rainflow([-2 1 -3 5 -1 3 -4 4 -3 1 -2 3 2 6])
q =
0.5000 3.0000 -0.5000 1.0000 2.0000
0.5000 4.0000 -1.0000 2.0000 3.0000
1.0000 4.0000 1.0000 5.0000 6.0000
0.5000 8.0000 1.0000 3.0000 4.0000
1.0000 3.0000 -0.5000 10.0000 11.0000
1.0000 1.0000 2.5000 12.0000 13.0000
1.0000 7.0000 0.5000 8.0000 9.0000
0.5000 9.0000 0.5000 4.0000 7.0000
0.5000 10.0000 1.0000 7.0000 14.0000参照
[1] ASTM E1049-85(2017), "Standard Practices for Cycle Counting in Fatigue Analysis." West Conshohocken, PA: ASTM International, 2017, https://www.astm.org/e1049-85r17.html.
拡張機能
バージョン履歴
R2017b で導入