histcounts2

二変量ヒストグラムのビンのカウント数

構文

[N,Xedges,Yedges] = histcounts2(X,Y)

[N,Xedges,Yedges] = histcounts2(X,Y,nbins)

[N,Xedges,Yedges] = histcounts2(X,Y,Xedges,Yedges)

[N,Xedges,Yedges] = histcounts2(___,Name,Value)

[N,Xedges,Yedges,binX,binY] = histcounts2(___)

説明

[N,Xedges,Yedges] = histcounts2(X,Y) は、X および Y の値を 2 次元のビンに分割し、各次元のビンのカウント数とビンのエッジを返します。関数 histcounts2 は、均一なビンを返す自動ビン化アルゴリズムを使用します。X と Y の値の範囲をカバーし、分布の基本的な形状を明らかにするビンが選択されます。

[N,Xedges,Yedges] = histcounts2(X,Y,nbins) は、各次元に使用するビンの数を指定します。

[N,Xedges,Yedges] = histcounts2(X,Y,Xedges,Yedges) は、Xedges と Yedges で指定されたビンのエッジを使用して、X と Y をビンに分割します。

[N,Xedges,Yedges] = histcounts2(___,Name,Value) は、前述の任意の構文について名前と値の引数を 1 つ以上使用して、追加のパラメーターを指定します。たとえば、BinWidth を 2 要素ベクトルとして指定して、各次元のビンの幅を調整します。

[N,Xedges,Yedges,binX,binY] = histcounts2(___) は、X と Y の対応する要素のビンのインデックスも返します。

例

ビンのカウント数とビンのエッジ

100 組の乱数ペアをビンに分配します。histcounts2 は自動的に、データの基となる分布が明らかになる適切なビンの幅を選択します。

x = randn(100,1);
y = randn(100,1);
[N,Xedges,Yedges] = histcounts2(x,y)

N = 7×6

     0     0     0     2     0     0
     1     2    10     4     0     0
     1     4     9     9     5     0
     1     4    10    11     5     1
     1     4     6     3     1     1
     0     0     1     2     0     0
     0     0     1     0     1     0

Xedges = 1×8

    -3    -2    -1     0     1     2     3     4

Yedges = 1×7

    -3    -2    -1     0     1     2     3

各次元のビンの数を指定

10 組の数値のペアを 12 個のビンに分配します。ビンを x 次元に 3 個、y 次元に 4 個指定します。

x = [1 1 2 3 2 2 1 1 2 3];
y = [5 6 3 8 9 1 2 7 5 1];
nbins = [3 4];
[N,Xedges,Yedges] = histcounts2(x,y,nbins)

N = 3×4

     1     0     2     1
     1     1     1     1
     1     0     0     1

Xedges = 1×4

    0.6000    1.4000    2.2000    3.0000

Yedges = 1×5

         0    2.3000    4.6000    6.9000    9.2000

ビン エッジの指定

1,000 組の乱数ペアをビンに分配します。x 次元と y 次元に 1 つずつ、計 2 つのベクトルでビンのエッジを定義します。各ベクトルの最初の要素は最初のビンの最初のエッジを指定し、最後の要素は最後のビンの最後のエッジを指定します。

x = randn(1000,1);
y = randn(1000,1);
Xedges = -5:5;
Yedges = [-5 -4 -2 -1 -0.5 0 0.5 1 2 4 5];
N = histcounts2(x,y,Xedges,Yedges)

N = 10×10

     0     0     0     0     0     0     0     0     0     0
     0     0     0     0     1     1     1     0     0     0
     0     0     5     5     3     5     1     2     0     0
     0     2    19    23    29    25    26    20     5     0
     0    10    36    51    59    71    54    46    10     0
     0     7    43    46    79    64    60    46     9     0
     0     3    12    18    21    23    19     9     6     0
     0     0     5     3     2     8     2     2     0     0
     0     0     0     1     1     1     0     0     0     0
     0     0     0     0     0     0     0     0     0     0

正規化されたビンのカウント数

1,000 組の乱数ペアをビンに分配します。Normalization を 'probability' に指定して、sum(N(:)) が 1 になるようにビンのカウント数を正規化します。つまり、それぞれのビンのカウント数は、観測値がそのビンに入る確率を表します。

x = randn(1000,1);
y = randn(1000,1);
[N,Xedges,Yedges] = histcounts2(x,y,6,'Normalization','probability')

N = 6×6

         0         0    0.0020    0.0020         0         0
         0    0.0110    0.0320    0.0260    0.0070    0.0010
    0.0010    0.0260    0.1410    0.1750    0.0430    0.0060
         0    0.0360    0.1620    0.1940    0.0370    0.0040
         0    0.0040    0.0300    0.0370    0.0100    0.0010
         0    0.0030    0.0040    0.0040    0.0010         0

Xedges = 1×7

   -4.0000   -2.7000   -1.4000   -0.1000    1.2000    2.5000    3.8000

Yedges = 1×7

   -4.0000   -2.7000   -1.4000   -0.1000    1.2000    2.5000    3.8000

ビン配置の判別

-10 ～ 10 の範囲にある 1,000 組の乱数の整数ペアをビンに分配します。BinMethod を 'integers' に指定して、整数を中心とする単位幅のビンを使用します。histcounts2 に出力を 5 つ指定して、データのビン配置を表すベクトルを返します。

x = randi([-10,10],1000,1);
y = randi([-10,10],1000,1);
[N,Xedges,Yedges,binX,binY] = histcounts2(x,y,'BinMethod','integers');

値 (x(3),y(3)) が分配されるビンを求めます。

[x(3),y(3)]

ans = 1×2

    -8    10

bin = [binX(3) binY(3)]

bin = 1×2

     3    21

入力引数

X,Y — ビンに分散させるデータ (個別の引数として指定)

ベクトル | 行列 | 多次元配列

ビンに分散させるデータ。ベクトル、行列または多次元配列の個別の引数として指定します。X と Y は同じサイズでなければなりません。

X および Y の対応する要素は、2 次元データ点の x 座標および y 座標 [X(k),Y(k)] を指定します。X と Y は異なるデータ型にすることができます。

histcounts2 はすべての NaN 値を無視します。同様にビンのエッジとして明示的に Inf または -Inf を指定しない限り、histcounts2 は Inf 値および -Inf 値を無視します。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical

nbins — 各次元のビンの数

正の整数スカラー | 正の整数の 2 要素ベクトル

各次元のビンの数。正のスカラー整数、あるいは正の整数の 2 要素ベクトルとして指定します。

• nbins がスカラーの場合、histcounts2 は各次元でその数のビンを使用します。

• nbins がベクトルの場合、最初の要素は x 次元のビンの数を指定し、2 番目の要素は y 次元のビンの数を指定します。

nbins を指定しない場合、histcounts2 は X と Y の値に基づいて使用するビンの数を自動的に計算します。

nbins を BinMethod または BinWidth と一緒に指定した場合、histcounts2 は最後のパラメーターのみに従います。

例: [N,Xedges,Yedges] = histcounts2(X,Y,15) は x 次元と y 次元で 15 個のビンを使用します。

例: [N,Xedges,Yedges] = histcounts2(X,Y,[15 20]) は x 次元で 15 個のビン、y 次元で 20 個のビンを使用します。

Xedges — x 次元のビンのエッジ

ベクトル

x 次元のビンのエッジ。ベクトルとして指定します。最初の要素は、x 次元の最初のビンの先頭のエッジを指定します。最後の要素は、x 次元の最後のビンの後方のエッジを指定します。後方のエッジは最後のビンにのみ含まれます。

• Xedges と Yedges を BinMethod、BinWidth、または NumBins と一緒に指定した場合、histcounts2 はビンのエッジのみに従い、ビンのエッジは最後に指定する必要があります。

• Xedges を XBinLimits と一緒に指定した場合、histcounts2 は Xedges のみに従い、Xedges は最後に指定する必要があります。

Yedges — y 次元のビンのエッジ

ベクトル

y 次元のビンのエッジ。ベクトルとして指定します。最初の要素は、y 次元の最初のビンの先頭のエッジを指定します。最後の要素は、y 次元の最後のビンの後方のエッジを指定します。後方のエッジは最後のビンにのみ含まれます。

• Yedges と Xedges を BinMethod、BinWidth、または NumBins と一緒に指定した場合、histcounts2 はビンのエッジのみに従い、ビンのエッジは最後に指定する必要があります。

• Yedges を YBinLimits と一緒に指定した場合、histcounts2 は Yedges のみに従い、Yedges は最後に指定する必要があります。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、コンマを使用して名前と値をそれぞれ区切り、Name を引用符で囲みます。

例: [N,Xedges,Yedges] = histcounts2(X,Y,'Normalization','probability') は、sum(N) が 1 になるようにビンのカウント数を N で正規化します。

BinWidth — 各次元のビンの幅

正の値の 2 要素ベクトル

各次元のビンの幅。正の値の 2 要素ベクトルとして指定します。最初の要素は x 次元のビンの幅を指定し、2 番目の要素は y 次元のビンの幅を指定します。

BinWidth を指定した場合、histcounts2 は各次元で最大 1024 (2¹⁰) 個のビンを使用できます。指定したビンの幅によってさらに多くのビンが必要となる場合、histcounts2 はビンの最大数に対応する、より大きなビンの幅を使用します。

BinWidth を BinMethod または NumBins と一緒に指定した場合、histcounts2 は最後のパラメーターのみに従います。

例: histcounts2(X,Y,'BinWidth',[5 10]) は x 次元のサイズが 5、y 次元のサイズが 10 のビンを使用します。

XBinLimits — x 次元のビンの範囲

2 要素ベクトル

x 次元のビンの範囲。2 要素ベクトル [xbmin,xbmax] として指定します。最初の要素は、x 次元の最初のビンのエッジを示します。2 番目の要素は、x 次元の最後のビンのエッジを示します。

このオプションを使用すると、ビンの範囲 X>=xbmin & X<=xbmax に含まれるデータのみがビンに入れられます。

YBinLimits — y 次元のビンの範囲

2 要素ベクトル

y 次元のビンの範囲。2 要素ベクトル [ybmin,ybmax] として指定します。最初の要素は、y 次元の最初のビンのエッジを示します。2 番目の要素は、y 次元の最後のビンのエッジを示します。

このオプションを使用すると、ビンの範囲 Y>=ybmin & Y<=ybmax に含まれるデータのみがビンに入れられます。

BinMethod — ビン化アルゴリズム

'auto' (既定値) | 'scott' | 'fd' | 'integers'

ビン化アルゴリズム。次の表のいずれかの値を指定します。

値	説明
'auto'	既定値の 'auto' アルゴリズムは、データの範囲をカバーするビンの幅を選択することで、基となる分布の形状を明らかにします。
'scott'	スコットの法則はデータが正規分布に近い場合に最適です。この規則は他の多くの分布にも適しています。ビンのサイズとして [3.5*std(X(:))*numel(X)^(-1/4), 3.5*std(Y(:))*numel(Y)^(-1/4)] を使用します。
'fd'	Freedman-Diaconis の法則は、データの外れ値の影響を受けにくく、裾が大きい分布をもつデータにより適しています。ビンのサイズとして [2*iqr(X(:))*numel(X)^(-1/4), 2*iqr(Y(:))*numel(Y)^(-1/4)] を使用します。X に極端な外れ値がある場合は [0.2*(max(X(:))-min(X(:)))*numel(X)^(-1/4), 0.2*(max(Y(:))-min(Y(:)))*numel(Y)^(-1/4)] を使用します。
'integers'	整数ルールは整数のペアを中心にしてビンを作成するので、整数データの場合に便利です。各次元に幅が 1 のビンを使用し、ビンのエッジを整数の中間に設定します。 誤って多すぎるビンを作成しないように、このルールを使用して作成するビンを 1024 (210) 個以下に制限できます。いずれかの次元のデータの範囲が 1024 よりも大きい場合、整数ルールは代わりに幅の広いビンを使用します。

• histcounts2 は、これらの式を厳密に使用するのではなく、ビンのエッジが "きりのよい" 数字になるように、ビンの数をわずかに調整します。

• NumBins、XBinEdges、YBinEdges、BinWidth、XBinLimits、または YBinLimits プロパティを設定した場合、BinMethod は 'manual' に設定されます。

• BinMethod を BinWidth または NumBins と一緒に指定した場合、histcounts2 は最後のパラメーターのみに従います。

例: histcounts2(X,Y,'BinMethod','integers') は 2 次元ビンの中心を各整数ペアとします。

Normalization — 正規化のタイプ

'count' (既定値) | 'probability' | 'percentage' | 'countdensity' | 'cumcount' | 'pdf' | 'cdf'

正規化のタイプ。次の表のいずれかの値を指定します。各ビン i に対して次のようになります。

• $$v_i$$ はビンの値です。

• $$c_i$$ はビン内の要素数です。

• $$A_i=w_{xi}\cdot w_{yi}$$ はビンの面積で、ビンの幅 x と y を使用して計算されます。

• $$N$$ は入力データ内の要素数です。データに欠損値が含まれる場合、または一部のデータがビンの範囲外にある場合、この値はビン化されたデータより大きくなることがあります。

値	ビンの値	メモ
'count' (既定)	$$v_i=c_i$$	観測のカウント数または頻度。 ビンの値の合計は最大で numel(X) および numel(y) です。合計がこれより小さくなるのは、一部の入力データがビンに含まれていない場合のみです。
'probability'	$$v_i=\frac{c_i}{N}$$	相対的確率。 入力データの要素の総数に対する各ビンの要素数は、最大で 1 です。
'percentage'	$$v_i=100*\frac{c_i}{N}$$	相対的割合。 各ビンの要素の割合は最大で 100 です。
'countdensity'	$$v_i=\frac{c_i}{A_i}$$	ビンの領域でスケーリングされたカウント数または頻度。 N(end,end) は最大で numel(X) および numel(Y) です。
'cumcount'	$$v_i={\displaystyle \sum _{j=1}^i{c}_j}$$	累積カウント数、つまり x 次元と y 次元の両方の各ビンとそれ以前のすべてのビンの観測数です。 N(end,end) は最大で numel(X) および numel(Y) です。
'pdf'	$$v_i=\frac{c_i}{N\cdot A_i}$$	確率密度関数の推定値です。 ビンの合計ボリュームは最大で 1 です。
'cdf'	$$v_i={\displaystyle \sum _{j=1}^i\frac{c_j}{N}}$$	累積分布関数の推定値です。 N(end,end) は最大で 1 です。

例: histcounts2(X,Y,'Normalization','pdf') は、確率密度関数の推定値を使用してデータをビン化します。

出力引数

N — ビンのカウント数

配列

ビンのカウント数。配列として返されます。

ビン化スキームでは、各ビンの先頭の x 次元と y 次元のエッジに加え、x 次元と y 次元の最後のビンに対する後方のエッジが含められます。

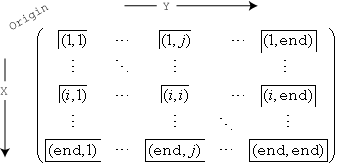
たとえば、(1,1) のビンは各次元の最初のエッジ上にある値を含み、右下の最後のビンはその任意のエッジ上にある値をすべて含みます。

Xedges — x 次元のビンのエッジ

ベクトル

x 次元のビンのエッジ。ベクトルとして返されます。最初の要素は、x 次元の最初のビンの先頭のエッジです。最後の要素は、x 次元の最後のビンの後方のエッジです。

Yedges — y 次元のビンのエッジ

ベクトル

y 次元のビンのエッジ。ベクトルとして返されます。最初の要素は、y 次元の最初のビンの先頭のエッジです。最後の要素は、y 次元の最後のビンの後方のエッジです。

binX — x 次元のビン インデックス

配列

x 次元のビン インデックス。X と同じサイズの配列として返されます。binX および binY の対応する要素は、X および Y の対応する値を含む番号付きビンを表します。binX または binY に値 0 が含まれる場合、これは要素がいずれのビンにも属さないことを示します (NaN 値など)。

たとえば、binX(1) および binY(1) は値 [X(1),Y(1)] のビンの位置を表します。

binY — y 次元のビン インデックス

配列

y 次元のビン インデックス。Y と同じサイズの配列として返されます。binX および binY の対応する要素は、X および Y の対応する値を含む番号付きビンを表します。binX または binY に値 0 が含まれる場合、これは要素がいずれのビンにも属さないことを示します (NaN 値など)。

たとえば、binX(1) および binY(1) は値 [X(1),Y(1)] のビンの位置を表します。

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

• コード生成では、この関数のスパース行列入力はサポートされません。

• ビンのエッジを指定しない場合、コード生成で可変サイズ配列および動的メモリ割り当てが必要になることがあります。

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数はスレッドベースの環境を完全にサポートしています。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

バージョン履歴

R2015b で導入

R2023b: パーセンテージを使用した正規化

名前と値の引数 Normalization を 'percentage' に指定すると、ヒストグラムの値をパーセンテージとして正規化することができます。

参考

histogram | histcounts | discretize | histogram2 | morebins | fewerbins