hht

ヒルベルト・ファン変換

ページ内をすべて折りたたむ

構文

hs = hht(imf)

hs = hht(imf,fs)

[hs,f,t] = hht(___)

[hs,f,t,imfinsf,imfinse] = hht(___)

[___] = hht(___,Name=Value)

hht(___)

hht(___,freqlocation)

説明

例

hs = hht(imf) は、固有モード関数 imf によって指定される信号のヒルベルトスペクトル hs を返します。hs は、スペクトル成分が経時変化する信号の混成から成る信号の解析に役立ちます。hht を使用して信号のヒルベルトスペクトル解析を実行し、局在的な特徴を特定します。

例

hs = hht(imf,fs) は、fs のレートでサンプリングされた信号のヒルベルトスペクトル hs を返します。

例

[hs,f,t] = hht(___) は、hs に加えて周波数ベクトル f と時間ベクトル t を返します。これらの出力引数は、前のいずれの入力構文でも使用できます。

例

[hs,f,t,imfinsf,imfinse] = hht(___) は、信号の診断のために、固有モード関数の瞬時周波数 imfinsf と瞬間エネルギー imfinse も返します。

例

[___] = hht(___,Name=Value) では、1 つ以上の名前と値の引数で指定された追加オプションを使用して、ヒルベルトスペクトルパラメーターを推定します。

例

出力引数なしで hht(___) を使用すると、現在の Figure ウィンドウにヒルベルトスペクトルがプロットされます。この構文は、これより前の構文の任意の入力引数で使用できます。

hht(___,freqlocation) では、周波数軸の場所を指定するためにオプションの freqlocation 引数を使用してヒルベルトスペクトルをプロットします。既定の設定では、周波数は y 軸上に表されます。

例

すべて折りたたむ

二次チャープのヒルベルトスペクトル

ライブスクリプトを開く

ガウス変調二次チャープを生成します。2 kHz のサンプルレートと 2 秒の信号持続時間を指定します。

fs = 2000;
t = 0:1/fs:2-1/fs;
q = chirp(t-2,4,1/2,6,'quadratic',100,'convex').*exp(-4*(t-1).^2);
plot(t,q)

Figure contains an axes object. The axes object contains an object of type line.

emd を使用して、固有モード関数 (IMF) と残差を可視化します。

emd(q)

信号の IMF を計算します。'Display' の名前と値のペアを使用して、各 IMF のふるい分け反復の数、相対許容誤差、およびふるい分け停止基準を示すテーブルを出力します。

imf = emd(q,'Display',1);

Current IMF  |  #Sift Iter  |  Relative Tol  |  Stop Criterion Hit  
      1      |        2     |    0.0063952   |  SiftMaxRelativeTolerance
      2      |        2     |       0.1007   |  SiftMaxRelativeTolerance
      3      |        2     |      0.01189   |  SiftMaxRelativeTolerance
      4      |        2     |    0.0075124   |  SiftMaxRelativeTolerance
Decomposition stopped because the number of extrema in the residual signal is less than the 'MaxNumExtrema' value.

計算された IMF を使用して、二次チャープのヒルベルトスペクトルをプロットします。周波数範囲を 0 Hz ～ 20 Hz に制限します。

hht(imf,fs,'FrequencyLimits',[0 20])

Figure contains an axes object. The axes object with title Hilbert Spectrum, xlabel Time (s), ylabel Frequency (Hz) contains 4 objects of type patch.

経験的モード分解の実行と信号のヒルベルトスペクトルの可視化

ライブスクリプトを開く

周波数にはっきりした変化が含まれる正弦波で構成される非定常連続信号を読み込み、可視化します。ジャックハンマーの振動と花火の音は、非定常連続信号の例です。信号は fs のレートでサンプリングされています。

load("sinusoidalSignalExampleData.mat","X","fs")
t = (0:length(X)-1)/fs;

plot(t,X)
xlabel("Time (s)")

Figure contains an axes object. The axes object with xlabel Time (s) contains an object of type line.

混合信号には異なる振幅と周波数値をもつ正弦波が含まれます。

ヒルベルトスペクトルプロットを作成するには、信号の固有モード関数 (IMF) が必要です。経験的モード分解を実行して、IMF と信号の残差を計算します。信号が滑らかではないため、'pchip' を内挿法として指定します。

[imf,residual,info] = emd(X,Interpolation="pchip");

コマンドウィンドウ内に生成されたテーブルは、生成された各 IMF のふるい分け反復の数、相対許容誤差、およびふるい分け停止基準を示します。この情報は info にも含まれます。名前と値のペア 'Display',0 を追加してテーブルを非表示にできます。

経験的モード分解を使用して取得した imf 成分を使用してヒルベルトスペクトルプロットを作成します。

hht(imf,fs)

Figure contains an axes object. The axes object with title Hilbert Spectrum, xlabel Time (s), ylabel Frequency (Hz) contains 9 objects of type patch.

周波数対時間のプロットは、IMF の各点における瞬間エネルギーを示す垂直方向のカラーバーがあるスパースプロットです。このプロットは、元の混合信号から分解された各成分の瞬時周波数スペクトルを表します。プロットには 1 秒での周波数に明瞭な変化がある 3 つの IMF が表示されます。

クジラの歌のヒルベルトスペクトル

ライブスクリプトを開く

4 kHz でサンプリングされた太平洋のシロナガスクジラのオーディオデータを含むファイルを読み込みます。ファイルは、コーネル大学の生物音響学研究プログラムが管理する動物発声ライブラリのものです。データの時間スケールは、音の高さを上げ鳴き声を聞き取りやすくするために係数 10 で圧縮されています。信号を MATLAB® の timetable に変換し、プロットします。信号のノイズの中で 4 つの特徴が目立っています。最初は "ふるえ声"、他の 3 つは "うめき声" として知られています。

[w,fs] = audioread('bluewhale.wav');
whale = timetable(w,'SampleRate',fs);
stackedplot(whale);

Figure contains an object of type stackedplot.

emd を使用して、最初の 3 つの固有モード関数 (IMF) と残差を可視化します。

emd(whale,'MaxNumIMF',3)

信号の最初の 3 つの IMF を計算します。'Display' の名前と値のペアを使用して、各 IMF のふるい分け反復の数、相対許容誤差、およびふるい分け停止基準を示すテーブルを出力します。

imf = emd(whale,'MaxNumIMF',3,'Display',1);

Current IMF  |  #Sift Iter  |  Relative Tol  |  Stop Criterion Hit  
      1      |        1     |      0.13523   |  SiftMaxRelativeTolerance
      2      |        2     |     0.030198   |  SiftMaxRelativeTolerance
      3      |        2     |      0.01908   |  SiftMaxRelativeTolerance
Decomposition stopped because maximum number of intrinsic mode functions was extracted.

計算された IMF を使用して、信号のヒルベルトスペクトルをプロットします。周波数範囲を 0 Hz ～ 1400 Hz に制限します。

hht(imf,'FrequencyLimits',[0 1400])

Figure contains an axes object. The axes object with title Hilbert Spectrum, xlabel Time (s), ylabel Frequency (Hz) contains 3 objects of type patch.

同じ周波数の範囲のヒルベルトスペクトルを計算します。ふるえ声とうめき声のヒルベルトスペクトルをメッシュプロットとして可視化します。

[hs,f,t] = hht(imf,'FrequencyLimits',[0 1400]);

mesh(seconds(t),f,hs,'EdgeColor','none','FaceColor','interp')
xlabel('Time (s)')
ylabel('Frequency (Hz)')
zlabel('Instantaneous Energy')

Figure contains an axes object. The axes object with xlabel Time (s), ylabel Frequency (Hz) contains an object of type surface.

信号のヒルベルトスペクトルパラメーターの計算

ライブスクリプトを開く

load("sinusoidalSignalExampleData.mat","X","fs")
t = (0:length(X)-1)/fs;

plot(t,X)
xlabel("Time (s)")

Figure contains an axes object. The axes object with xlabel Time (s) contains an object of type line.

混合信号には異なる振幅と周波数値をもつ正弦波が含まれます。

ヒルベルトスペクトルパラメーターを計算するには、信号の IMF が必要です。経験的モード分解を実行して、固有モード関数と信号の残差を計算します。信号が滑らかではないため、'pchip' を内挿法として指定します。

[imf,residual,info] = emd(X,Interpolation="pchip");

コマンドウィンドウ内に生成されたテーブルは、生成された各 IMF のふるい分け反復の数、相対許容誤差、およびふるい分け停止基準を示します。この情報は info にも含まれます。'Display' を 0 と指定することによってテーブルを非表示にできます。

ヒルベルトスペクトルの次のパラメーターを計算します。ヒルベルトスペクトル hs、周波数ベクトル f、時間ベクトル t、瞬時周波数 imfinsf および瞬間エネルギー imfinse。

[hs,f,t,imfinsf,imfinse] = hht(imf,fs);

計算したヒルベルトスペクトルパラメーターを時間-周波数解析と信号の診断に使用します。

多成分信号の VMD

ライブスクリプトを開く

周波数 2 Hz、10 Hz、および 30 Hz の 3 つの正弦波からなる多成分信号を生成します。正弦波は 1 kHz で 2 秒間サンプリングされます。分散 0.01² のホワイトガウスノイズに信号を組み込みます。

fs = 1e3;
t = 1:1/fs:2-1/fs;
x = cos(2*pi*2*t) + 2*cos(2*pi*10*t) + 4*cos(2*pi*30*t) + 0.01*randn(1,length(t));

ノイズ信号の IMF を計算し、それを 3 次元プロットで可視化します。

imf = vmd(x);
[p,q] = ndgrid(t,1:size(imf,2));
plot3(p,q,imf)
grid on
xlabel('Time Values')
ylabel('Mode Number')
zlabel('Mode Amplitude')

Figure contains an axes object. The axes object with xlabel Time Values, ylabel Mode Number contains 5 objects of type line.

計算された IMF を使用して、多成分信号のヒルベルトスペクトルをプロットします。周波数範囲を [0, 40] Hz に制限します。

hht(imf,fs,'FrequencyLimits',[0,40])

Figure contains an axes object. The axes object with title Hilbert Spectrum, xlabel Time (s), ylabel Frequency (Hz) contains 5 objects of type patch.

振動信号のヒルベルトスペクトルの計算

ライブスクリプトを開く

破損したベアリングの振動信号をシミュレートします。この信号のヒルベルトスペクトルを計算し、欠陥を探します。

ピッチの直径が 12 cm のベアリングは 8 つの回転要素を持ちます。各回転要素の直径は 2 cm です。内輪が 1 秒あたり 25 回駆動される間、外輪は静止状態を保ちます。加速度計はベアリングの振動を 10 kHz でサンプリングします。

fs = 10000;
f0 = 25;
n = 8;
d = 0.02;
p = 0.12;

正常なベアリングの振動信号には、駆動点周波数の次数が複数含まれます。

t = 0:1/fs:10-1/fs;
yHealthy = [1 0.5 0.2 0.1 0.05]*sin(2*pi*f0*[1 2 3 4 5]'.*t)/5;

共振は、測定プロセス中にベアリングの振動で励起されます。

yHealthy = (1+1./(1+linspace(-10,10,length(yHealthy)).^4)).*yHealthy;

共振によりベアリングの外輪に欠陥が生じることで、摩耗が進行します。欠陥があると、ベアリングの外輪転動体通過周波数 (BPFO) で繰り返される一連の影響を引き起こします。

$B P F O = \frac{1}{2} n f_{0} [1 - \frac{d}{p} \cos θ],$

ここで、 $f_{0}$ は駆動レート、 $n$ は回転要素の数、 $d$ は回転要素の直径、 $p$ はベアリングのピッチの直径、 $θ$ はベアリングの接触角です。接触角は 15° と仮定して BPFO を計算します。

ca = 15;
bpfo = n*f0/2*(1-d/p*cosd(ca));

関数pulstranを使用して、影響を 5 ミリ秒の正弦波の周期列としてモデル化します。3 kHz の各正弦波に、フラットトップウィンドウによってウィンドウが適用されます。べき乗則を使用して、ベアリング振動信号に進行する摩耗を導入します。

fImpact = 3000;
tImpact = 0:1/fs:5e-3-1/fs;
wImpact = flattopwin(length(tImpact))'/10;
xImpact = sin(2*pi*fImpact*tImpact).*wImpact;

tx = 0:1/bpfo:t(end);
tx = [tx; 1.3.^tx-2];

nWear = 49000;
nSamples = 100000;
yImpact = pulstran(t,tx',xImpact,fs)/5;
yImpact = [zeros(1,nWear) yImpact(1,(nWear+1):nSamples)];

正常なベアリング信号に影響を追加して BPFO 振動信号を生成します。信号をプロットし、5.0 秒目から始まる 0.3 秒区間を選択します。

yBPFO = yImpact + yHealthy;

xLimLeft = 5.0;
xLimRight = 5.3;
yMin = -0.6;
yMax = 0.6;

plot(t,yBPFO)

hold on
[limLeft,limRight] = meshgrid([xLimLeft xLimRight],[yMin yMax]);
plot(limLeft,limRight,'--')
hold off

Figure contains an axes object. The axes object contains 3 objects of type line.

選択した区間にズームインして、影響の効果を可視化します。

xlim([xLimLeft xLimRight])

Figure contains an axes object. The axes object contains 3 objects of type line.

ホワイトガウスノイズを信号に付加します。 $1 / 15 0^{2}$ のノイズ分散を指定します。

rn = 150;
yGood = yHealthy + randn(size(yHealthy))/rn;
yBad = yBPFO + randn(size(yHealthy))/rn;

plot(t,yGood,t,yBad)
xlim([xLimLeft xLimRight])
legend("Healthy","Damaged")

Figure contains an axes object. The axes object contains 2 objects of type line. These objects represent Healthy, Damaged.

emdを使用して、正常なベアリング信号の経験的モード分解を実行します。最初の 5 つの固有モード関数 (IMF) を計算します。'Display' の名前と値の引数を使用して、各 IMF のふるい分け反復の数、相対許容誤差、およびふるい分け停止基準を示すテーブルを出力します。

imfGood = emd(yGood,MaxNumIMF=5,Display=1);

Current IMF  |  #Sift Iter  |  Relative Tol  |  Stop Criterion Hit  
      1      |        3     |     0.017132   |  SiftMaxRelativeTolerance
      2      |        3     |      0.12694   |  SiftMaxRelativeTolerance
      3      |        6     |      0.14582   |  SiftMaxRelativeTolerance
      4      |        1     |     0.011082   |  SiftMaxRelativeTolerance
      5      |        2     |      0.03463   |  SiftMaxRelativeTolerance
Decomposition stopped because maximum number of intrinsic mode functions was extracted.

emd を出力引数なしで使用し、最初の 3 つの IMF と残差を可視化します。

emd(yGood,MaxNumIMF=5)

欠陥のあるベアリング信号の IMF を計算および可視化します。最初の経験的モードでは、高周波数に影響が見られます。この高周波数モードでは、摩耗が進行するにつれてエネルギーが増加します。

imfBad = emd(yBad,MaxNumIMF=5,Display=1);

Current IMF  |  #Sift Iter  |  Relative Tol  |  Stop Criterion Hit  
      1      |        2     |     0.041274   |  SiftMaxRelativeTolerance
      2      |        3     |      0.16695   |  SiftMaxRelativeTolerance
      3      |        3     |      0.18428   |  SiftMaxRelativeTolerance
      4      |        1     |     0.037177   |  SiftMaxRelativeTolerance
      5      |        2     |     0.095861   |  SiftMaxRelativeTolerance
Decomposition stopped because maximum number of intrinsic mode functions was extracted.

emd(yBad,MaxNumIMF=5)

欠陥のあるベアリング信号について、最初の経験的モードのヒルベルトスペクトルをプロットします。最初のモードは、高周波数の影響の効果をとらえています。ベアリングの摩耗が進行するにつれて、影響のエネルギーが増加します。

figure
hht(imfBad(:,1),fs)

Figure contains an axes object. The axes object with title Hilbert Spectrum, xlabel Time (s), ylabel Frequency (Hz) contains an object of type patch.

3 番目のモードのヒルベルトスペクトルは、振動信号の共振を示します。周波数範囲を 0 Hz ～ 100 Hz に制限します。

hht(imfBad(:,3),fs,FrequencyLimits=[0 100])

Figure contains an axes object. The axes object with title Hilbert Spectrum, xlabel Time (s), ylabel Frequency (Hz) contains an object of type patch.

比較のために、正常なベアリング信号について、最初と 3 番目のモードのヒルベルトスペクトルをプロットします。

subplot(2,1,1)
hht(imfGood(:,1),fs)
subplot(2,1,2)
hht(imfGood(:,3),fs,FrequencyLimits=[0 100])

Figure contains 2 axes objects. Axes object 1 with title Hilbert Spectrum, xlabel Time (s), ylabel Frequency (Hz) contains an object of type patch. Axes object 2 with title Hilbert Spectrum, xlabel Time (s), ylabel Frequency (Hz) contains an object of type patch.

入力引数

すべて折りたたむ

`imf` — 固有モード関数
行列 | timetable

固有モード関数。行列または timetable として指定します。imf は、包絡線がゼロに関して対称であり、極値とゼロクロッシングの数の違いが多くても 1 つの信号です。emd は、複雑な信号をヒルベルトスペクトル解析を実行するために必要な固有モード関数の有限数に分解および単純化するために使用されます。

hht は、imf の各列を固有モード関数として処理します。imf の計算の詳細については、emd を参照してください。

`fs` — サンプルレート
`2π` (既定値) | 正のスカラー

サンプルレート。正のスカラーで指定します。fs が指定されない場合、2π の正規化された周波数がヒルベルトスペクトルの計算に使用されます。imf が timetable として指定されている場合、これからサンプルレートが推定されます。

`freqlocation` — プロット上の周波数軸の位置
`"yaxis"` (既定値) | `"xaxis"`

プロット上の周波数軸の位置。"yaxis" または "xaxis" として指定します。プロットの y 軸または x 軸上に周波数データを表示するには、それぞれ "yaxis" または "xaxis" として freqlocation を指定します。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、コンマを使用して名前と値をそれぞれ区切り、Name を引用符で囲みます。

例: 'FrequencyResolution',1

`FrequencyLimits` — ヒルベルトスペクトルを計算する周波数限界
`[0,fs/2]` (既定値) | 1 行 2 列の整数値のベクトル

ヒルベルトスペクトルを計算する周波数限界。1 行 2 列の整数値ベクトルとして指定します。FrequencyLimits は Hz で指定します。

`FrequencyResolution` — 周波数範囲を離散化する周波数分解能
(f_high-f_low)/100 (既定値) | 正のスカラー

周波数限界を離散化する周波数分解能。正のスカラーとして指定します。FrequencyResolution は Hz で指定します。FrequencyResolution が指定されない場合、(f_high-f_low)/100 の値は FrequencyLimits から推定されます。ここで、f_high は FrequencyLimits の上限、f_low は下限です。

`MinThreshold` — ヒルベルトスペクトルの最小しきい値
`-inf` (既定値) | スカラー

ヒルベルトスペクトルの最小しきい値。スカラーとして指定します。MinThreshold は、 $10 \log_{10} (h s)$ の対応する要素が MinThreshold より小さい場合に hs の要素を 0 に設定します。

出力引数

すべて折りたたむ

`hs` — 信号のヒルベルトスペクトル
スパース行列

信号のヒルベルトスペクトル。スパース行列として返されます。hs を使用して時間-周波数を解析し、信号の局在的な特徴を特定します。

`f` — 周波数値
ベクトル

信号の周波数値。ベクトルとして返されます。hht は、周波数ベクトル f と時間ベクトル t を使用してヒルベルトスペクトルプロットを作成します。

数学的には、f は f = f_low : f_res : f_high と表されます。ここで、f_res は周波数分解能です。

`t` — 時間値
ベクトル | `duration` 配列

信号の時間値。ベクトルまたは duration 配列として返されます。hht は、時間ベクトル t と周波数ベクトル f を使用してヒルベルトスペクトルプロットを作成します。

t は以下として返されます。

imf を配列として指定した場合は配列。
imf を等間隔サンプルの timetable として指定した場合は duration 配列。

`imfinsf` — 各 IMF の瞬時周波数
ベクトル | 行列 | timetable

各 IMF の瞬時周波数。ベクトル、行列、または timetable として返されます。

imfinsf は imf と同じ列数であり、以下として返されます。

imf をベクトルとして指定した場合はベクトル。
imf を行列として指定した場合は行列。
imf を等間隔サンプルの timetable として指定した場合は timetable。

`imfinse` — 各 IMF の瞬間エネルギー
ベクトル | 行列 | timetable

各 IMF の瞬間エネルギー。ベクトル、行列、または timetable として返されます。

imfinse は imf と同じ列数であり、以下として返されます。

imf をベクトルとして指定した場合はベクトル。
imf を行列として指定した場合は行列。
imf を等間隔サンプルの timetable として指定した場合は timetable。

アルゴリズム

ヒルベルト・ファン変換は、非定常および非線形データの時間-周波数解析の実行に役立ちます。ヒルベルト・ファン手順は以下のステップから構成されます。

emd または vmd はデータセット x を固有モード関数の有限個に分解します。
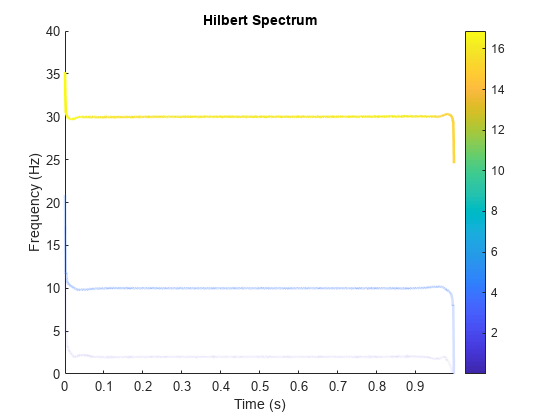
各固有モード関数 x_i の場合、関数 hht は次のとおりです。
1. hilbert を使用して解析信号 $z_{i} (t) = x_{i} (t) + j H {x_{i} (t)}$ を計算します。ここで、H{x_i} は x_i のヒルベルト変換です。
2. z_i を $z_{i} (t) = a_{i} (t) e^{j θ_{i} (t)}$ として表します。ここで、a_i(t) は瞬間的な振幅で、 $θ_{i} (t)$ は瞬間的な位相です。
3. 瞬間エネルギー $| a_{i} (t) |^{2}$ 、と瞬時周波数 $ω_{i} (t) \equiv d θ_{i} (t) / d t$ を計算します。サンプルレートを指定した場合、hht は、 $ω_{i} (t)$ を周波数 (Hz) に変換します。
4. imfinse の瞬間エネルギーと imfinsf の瞬時周波数を出力します。
出力引数なしで呼び出した場合、hht は、信号のエネルギーを、振幅に比例する色をもつ時間と周波数の関数としてプロットします。

参照

[1] Huang, Norden E, and Samuel S P Shen. Hilbert–Huang Transform and Its Applications. 2nd ed. Vol. 16. Interdisciplinary Mathematical Sciences. WORLD SCIENTIFIC, 2014. https://doi.org/10.1142/8804.

[2] Huang, Norden E., Zhaohua Wu, Steven R. Long, Kenneth C. Arnold, Xianyao Chen, and Karin Blank. “ON INSTANTANEOUS FREQUENCY.” Advances in Adaptive Data Analysis 01, no. 02 (April 2009): 177–229. https://doi.org/10.1142/S1793536909000096.

拡張機能

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

名前と値の引数はコンパイル時の定数でなければなりません。

バージョン履歴

R2018a で導入

参考

emd | hilbert | vmd

hht

構文

説明

例

二次チャープのヒルベルト スペクトル

経験的モード分解の実行と信号のヒルベルト スペクトルの可視化

クジラの歌のヒルベルト スペクトル

信号のヒルベルト スペクトル パラメーターの計算

多成分信号の VMD

振動信号のヒルベルト スペクトルの計算

入力引数

imf — 固有モード関数 行列 | timetable

fs — サンプル レート 2π (既定値) | 正のスカラー

freqlocation — プロット上の周波数軸の位置 "yaxis" (既定値) | "xaxis"

名前と値の引数

FrequencyLimits — ヒルベルト スペクトルを計算する周波数限界 [0,fs/2] (既定値) | 1 行 2 列の整数値のベクトル

FrequencyResolution — 周波数範囲を離散化する周波数分解能 (f_high-f_low)/100 (既定値) | 正のスカラー

MinThreshold — ヒルベルト スペクトルの最小しきい値 -inf (既定値) | スカラー

出力引数

hs — 信号のヒルベルト スペクトル スパース行列

f — 周波数値 ベクトル

t — 時間値 ベクトル | duration 配列

imfinsf — 各 IMF の瞬時周波数 ベクトル | 行列 | timetable

imfinse — 各 IMF の瞬間エネルギー ベクトル | 行列 | timetable

アルゴリズム

参照

拡張機能

C/C++ コード生成 MATLAB® Coder™ を使用して C および C++ コードを生成します。

バージョン履歴

参考

トピック

二次チャープのヒルベルトスペクトル

経験的モード分解の実行と信号のヒルベルトスペクトルの可視化

クジラの歌のヒルベルトスペクトル

信号のヒルベルトスペクトルパラメーターの計算

振動信号のヒルベルトスペクトルの計算

`imf` — 固有モード関数
行列 | timetable

`fs` — サンプルレート
`2π` (既定値) | 正のスカラー

`freqlocation` — プロット上の周波数軸の位置
`"yaxis"` (既定値) | `"xaxis"`

`FrequencyLimits` — ヒルベルトスペクトルを計算する周波数限界
`[0,fs/2]` (既定値) | 1 行 2 列の整数値のベクトル

`FrequencyResolution` — 周波数範囲を離散化する周波数分解能
(f_high-f_low)/100 (既定値) | 正のスカラー

`MinThreshold` — ヒルベルトスペクトルの最小しきい値
`-inf` (既定値) | スカラー

`hs` — 信号のヒルベルトスペクトル
スパース行列

`f` — 周波数値
ベクトル

`t` — 時間値
ベクトル | `duration` 配列

`imfinsf` — 各 IMF の瞬時周波数
ベクトル | 行列 | timetable

`imfinse` — 各 IMF の瞬間エネルギー
ベクトル | 行列 | timetable

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。