このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

emd

経験的モード分解

構文

[imf,residual] = emd(x)

[imf,residual,info] = emd(x)

[___] = emd(___,Name,Value)

emd(___)

説明

[imf,residual] = emd(x) は、x の経験的モード分解に対応する固有モード関数 imf と残差信号 residual を返します。emd を使用して、複雑な信号をヒルベルト スペクトル解析に必要な有限数の固有モード関数に分解して単純化します。

[imf,residual,info] = emd(x) は、診断の目的のために IMF の追加情報 info と残差信号を返します。

[___] = emd(___,Name,Value) では、1 つ以上の Name,Value のペア引数で指定された追加オプションを使用して、経験的モード分解を実行します。

emd(___) では、同じ Figure 内で元の信号、IMF、残差信号をサブプロットとしてプロットします。

例

経験的モード分解の実行と信号のヒルベルト スペクトルの可視化

周波数にはっきりした変化が含まれる正弦波で構成される非定常連続信号を読み込み、可視化します。ジャックハンマーの振動と花火の音は、非定常連続信号の例です。信号は fs のレートでサンプリングされています。

load("sinusoidalSignalExampleData.mat","X","fs")
t = (0:length(X)-1)/fs;

plot(t,X)
xlabel("Time (s)")

混合信号には異なる振幅と周波数値をもつ正弦波が含まれます。

ヒルベルト スペクトル プロットを作成するには、信号の固有モード関数 (IMF) が必要です。経験的モード分解を実行して、IMF と信号の残差を計算します。信号が滑らかではないため、'pchip' を内挿法として指定します。

[imf,residual,info] = emd(X,Interpolation="pchip");

コマンド ウィンドウ内に生成されたテーブルは、生成された各 IMF のふるい分け反復の数、相対許容誤差、およびふるい分け停止基準を示します。この情報は info にも含まれます。名前と値のペア 'Display',0 を追加してテーブルを非表示にできます。

経験的モード分解を使用して取得した imf 成分を使用してヒルベルト スペクトル プロットを作成します。

hht(imf,fs)

周波数対時間のプロットは、IMF の各点における瞬間エネルギーを示す垂直方向のカラー バーがあるスパース プロットです。このプロットは、元の混合信号から分解された各成分の瞬時周波数スペクトルを表します。プロットには 1 秒での周波数に明瞭な変化がある 3 つの IMF が表示されます。

正弦波の固有モード関数のゼロクロッシングと極値

この三角恒等式は、同じ物理量信号の 2 つの異なるビューを示します。

$\frac{5}{2}\mathrm{cos2}\pi {\mathit{f}}_1\mathit{t}+\frac{1}{4}(\mathrm{cos2}\pi \left({\mathit{f}}_1+{\mathit{f}}_2\right)t+\mathrm{cos2}\pi \left({\mathit{f}}_1-{\mathit{f}}_2\right)t)=(2+{\cos }^2\pi {\mathit{f}}_2\mathit{t})\mathrm{cos2}\pi {\mathit{f}}_1\mathit{t}$.

2 つの正弦波 s および z を生成します。s は 3 つの正弦波の和で、z は変調された振幅を持つ単一の正弦波です。これらの差の無限大ノルムを計算して、2 つの信号が等しいことを確認します。

t = 0:1e-3:10;
omega1 = 2*pi*100;
omega2 = 2*pi*20;
s = 0.25*cos((omega1-omega2)*t) + ...
    2.5*cos(omega1*t) + ...
    0.25*cos((omega1+omega2)*t);
z = (2+cos(omega2/2*t).^2).*cos(omega1*t);

norm(s-z,Inf) 

ans = 
3.2729e-13

正弦波をプロットし、2 秒目から始まる 1 秒区間を選択します。

plot(t,[s' z'])
xlim([2 3])
xlabel('Time (s)')
ylabel('Signal')

信号のスペクトログラムを取得します。スペクトログラムは、3 つの異なる正弦波成分を示しています。フーリエ解析では、信号を正弦波の重ね合わせと見なします。

pspectrum(s,1000,'spectrogram','TimeResolution',4)

emd を使用して、信号の固有モード関数 (IMF) と追加の診断情報を計算します。既定では、この関数は各 IMF のふるい分け反復の数、相対許容誤差、およびふるい分け停止基準を示すテーブルを出力します。経験的モード分解では、信号を z と見なします。

[imf,~,info] = emd(s);

ゼロクロッシングと局所的極値の数は、最大で 1 だけ異なります。これは、信号が IMF であるために必要な条件を満たしています。

info.NumZerocrossing - info.NumExtrema

ans = 
1

IMF をプロットし、2 秒目から始まる 0.5 秒区間を選択します。emd は信号を振幅変調された信号として表示するため、IMF は AM 信号です。

plot(t,imf)
xlim([2 2.5])
xlabel('Time (s)')
ylabel('IMF')

振動信号の固有モード関数の計算

破損したベアリングの振動信号をシミュレートします。経験的モード分解を実行して、信号の IMF を可視化し、欠陥を調査します。

ピッチの直径が 12 cm のベアリングは 8 つの回転要素を持ちます。各回転要素の直径は 2 cm です。内輪が 1 秒あたり 25 回駆動される間、外輪は静止状態を保ちます。加速度計はベアリングの振動を 10 kHz でサンプリングします。

fs = 10000;
f0 = 25;
n = 8;
d = 0.02;
p = 0.12;

健全なベアリングの振動信号には、駆動点周波数の次数が複数含まれます。

t = 0:1/fs:10-1/fs;
a = 0.2*[1 0.5 0.2 0.1 0.05];
f = f0*[1 2 3 4 5];
yHealthy = a*sin(2*pi*f'.*t);

共振は、測定プロセス中にベアリングの振動で励起されます。

yHealthy = (1+1./(1+linspace(-10,10,length(yHealthy)).^4)).*yHealthy;

共振によりベアリングの外輪に欠陥が生じることで、摩耗が進行します。欠陥があると、ベアリングの外輪転動体通過周波数 (BPFO) で繰り返される一連の影響を引き起こします。

$$BPFO=\frac{1}{2}n{f}_0[1-\frac{d}{p}\cos \theta ],$$

ここで、$$f_0$$ は駆動レート、$$n$$ は回転要素の数、$$d$$ は回転要素の直径、$$p$$ はベアリングのピッチの直径、$$\theta$$ はベアリングの接触角です。接触角は 15° と仮定して BPFO を計算します。

ca = 15;
bpfo = n*f0/2*(1-d/p*cosd(ca));

関数pulstranを使用して、影響を 5 ミリ秒の正弦波の周期列としてモデル化します。3 kHz の各正弦波に、フラット トップ ウィンドウによってウィンドウが適用されます。べき乗則を使用して、ベアリング振動信号に進行する摩耗を導入します。

fImpact = 3000;
tImpact = 0:1/fs:5e-3-1/fs;
wImpact = flattopwin(length(tImpact))'/10;
xImpact = sin(2*pi*fImpact*tImpact).*wImpact;

tx = 0:1/bpfo:t(end);
tx = [tx; 1.3.^tx-2];

nWear = 49000;
nSamples = 100000;
yImpact = pulstran(t,tx',xImpact,fs)/5;
yImpact = [zeros(1,nWear) yImpact(1,(nWear+1):nSamples)];

健全な信号に影響を追加して BPFO 振動信号を生成します。信号をプロットし、5.0 秒目から始まる 0.3 秒区間を選択します。

yBPFO = yImpact + yHealthy;

xLimLeft = 5.0;
xLimRight = 5.3;
yMin = -0.6;
yMax = 0.6;

plot(t,yBPFO)

hold on
[limLeft,limRight] = meshgrid([xLimLeft xLimRight],[yMin yMax]);
plot(limLeft,limRight,"--")
hold off
xlabel("Time (seconds)")
ylabel("Amplitude")

選択した区間にズームインして、影響の効果を可視化します。

xlim([xLimLeft xLimRight])

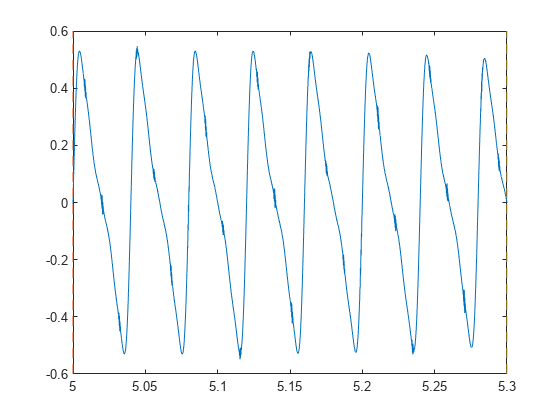
ホワイト ガウス ノイズを信号に付加します。$$1/150^2$$ のノイズ分散を指定します。

rn = 150;
yGood = yHealthy + randn(size(yHealthy))/rn;
yBad = yBPFO + randn(size(yHealthy))/rn;

plot(t,yGood,t,yBad)
xlim([xLimLeft xLimRight])
legend("Healthy","Damaged")
xlabel("Time (seconds)")
ylabel("Amplitude")

emd を使用して、健全なベアリング信号の経験的モード分解を実行します。最初の 5 つの固有モード関数 (IMF) を計算します。名前と値の引数 Display を使用して、各 IMF のふるい分け反復の数、相対許容誤差、およびふるい分け停止基準を示すテーブルを表示します。

imfGood = emd(yGood,MaxNumIMF=5,Display=1);

Current IMF  |  #Sift Iter  |  Relative Tol  |  Stop Criterion Hit  
      1      |        3     |     0.017132   |  SiftMaxRelativeTolerance
      2      |        3     |      0.12694   |  SiftMaxRelativeTolerance
      3      |        6     |      0.14582   |  SiftMaxRelativeTolerance
      4      |        1     |     0.011082   |  SiftMaxRelativeTolerance
      5      |        2     |      0.03463   |  SiftMaxRelativeTolerance
Decomposition stopped because maximum number of intrinsic mode functions was extracted.

emd を出力引数なしで使用し、最初の 3 つのモードと残差を可視化します。

emd(yGood,MaxNumIMF=5)

欠陥のあるベアリング信号の IMF を計算および可視化します。最初の経験的モードでは、高周波数に影響が見られます。この高周波数モードでは、摩耗が進行するにつれてエネルギーが増加します。3 番目のモードは、振動信号の共振を示します。

imfBad = emd(yBad,MaxNumIMF=5,Display=1);

Current IMF  |  #Sift Iter  |  Relative Tol  |  Stop Criterion Hit  
      1      |        2     |     0.041274   |  SiftMaxRelativeTolerance
      2      |        3     |      0.16695   |  SiftMaxRelativeTolerance
      3      |        3     |      0.18428   |  SiftMaxRelativeTolerance
      4      |        1     |     0.037177   |  SiftMaxRelativeTolerance
      5      |        2     |     0.095861   |  SiftMaxRelativeTolerance
Decomposition stopped because maximum number of intrinsic mode functions was extracted.

emd(yBad,MaxNumIMF=5)

解析の次の手順は、抽出された IMF のヒルベルト スペクトルを計算することです。詳細については、振動信号のヒルベルト スペクトルの計算の例を参照してください。

信号の残差および固有モード関数の可視化

周波数にはっきりした変化が含まれる正弦波で構成される非定常連続信号を読み込み、可視化します。ジャックハンマーの振動と花火の音は、非定常連続信号の例です。信号は fs のレートでサンプリングされています。

load("sinusoidalSignalExampleData.mat","X","fs")
t = (0:length(X)-1)/fs;
plot(t,X)
xlabel("Time(s)")

混合信号には異なる振幅と周波数値をもつ正弦波が含まれます。

経験的モード分解を実行して、固有モード関数と信号の残差をプロットします。信号が滑らかではないため、"pchip" を内挿法として指定します。

emd(X,Interpolation="pchip",Display=1)

Current IMF  |  #Sift Iter  |  Relative Tol  |  Stop Criterion Hit  
      1      |        2     |     0.026352   |  SiftMaxRelativeTolerance
      2      |        2     |    0.0039573   |  SiftMaxRelativeTolerance
      3      |        1     |     0.024838   |  SiftMaxRelativeTolerance
      4      |        2     |      0.05929   |  SiftMaxRelativeTolerance
      5      |        2     |      0.11317   |  SiftMaxRelativeTolerance
      6      |        2     |      0.12599   |  SiftMaxRelativeTolerance
      7      |        2     |      0.13802   |  SiftMaxRelativeTolerance
      8      |        3     |      0.15937   |  SiftMaxRelativeTolerance
      9      |        2     |      0.15923   |  SiftMaxRelativeTolerance
Decomposition stopped because the number of extrema in the residual signal is less than the 'MaxNumExtrema' value.

emd は、元の信号、最初の 3 つの IMF、残差信号を含む対話型の Figure を生成します。コマンド ウィンドウ内に生成されたテーブルは、生成された各 IMF のふるい分け反復の数、相対許容誤差、およびふるい分け停止基準を示します。名前と値の引数 Display を削除するか、これを 0 と指定することによって、テーブルを非表示にできます。

Figure 内の空白を右クリックし、[IMF セレクター] ウィンドウを開きます。[IMF セレクター] を使用して、生成された IMF、元の信号、および残差を選択的に表示します。

リストから表示する IMF を選択します。Figure に元の信号と残差を表示するかどうかを選択します。

これで、選択した IMF が Figure に表示されます。

Figure を使用して、残差と共に元の信号から分解された個々の成分を可視化します。残差は IMF の総数に対して計算され、[IMF セレクター] ウィンドウで選択された IMF によって変化はしないことに注意してください。

入力引数

x — 時間領域信号

ベクトル | timetable

時間領域信号。実数値のベクトル、または単一列の単一変数 timetable として指定します。x が timetable の場合、x は増加する有限の行時間を含んでいなければなりません。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、コンマを使用して名前と値をそれぞれ区切り、Name を引用符で囲みます。

例: 'MaxNumIMF',5

SiftRelativeTolerance — コーシー型収束基準

0.2 (既定値) | 正のスカラー

コーシー型収束基準。'SiftRelativeTolerance' と正のスカラーで構成されるコンマ区切りのペアとして指定します。SiftRelativeTolerance はふるい分け停止基準の 1 つです。つまり、現在の相対許容誤差が SiftRelativeTolerance 未満の場合にふるい分けが停止します。詳細については、ふるい分けの相対許容誤差を参照してください。

SiftMaxIterations — ふるい分け反復の最大数

100 (既定値) | 正のスカラー整数

ふるい分け反復の最大数。'SiftMaxIterations' と正のスカラー整数で構成されるコンマ区切りのペアとして指定します。SiftMaxIterations はふるい分け停止基準の 1 つです。つまり、現在の反復数が SiftMaxIterations より大きい場合にふるい分けが停止します。

SiftMaxIterations は 0 または正の整数のみを使用して指定できます。

MaxNumIMF — 抽出された IMF の最大数

10 (既定値) | 正のスカラー整数

抽出された IMF の最大数。'MaxNumIMF' と正のスカラー整数で構成されるコンマ区切りのペアとして指定します。MaxNumIMF は分解停止基準の 1 つです。つまり、生成された IMF の数が MaxNumIMF に等しい場合に分解が停止します。

MaxNumIMF は 0 または正の整数のみを使用して指定できます。

MaxNumExtrema — 残差信号の極値の最大数

1 (既定値) | 正のスカラー整数

残差信号の極値の最大数。'MaxNumExtrema' と正のスカラー整数で構成されるコンマ区切りのペアとして指定します。MaxNumExtrema は分解停止基準の 1 つです。つまり、極値の数が MaxNumExtrema 未満の場合に分解が停止します。

MaxNumExtrema は 0 または正の整数のみを使用して指定できます。

MaxEnergyRatio — 信号対残差エネルギー比

20 (既定値) | スカラー

信号対残差エネルギー比。'MaxEnergyRatio' とスカラーで構成されるコンマ区切りのペアとして指定します。MaxEnergyRatio はふるい分けの開始における信号のエネルギーと平均包絡線エネルギーとの比です。MaxEnergyRatio は分解停止基準の 1 つです。つまり、現在のエネルギー比が MaxEnergyRatio より大きい場合に分解が停止します。詳細については、エネルギー比を参照してください。

Interpolation — 包絡線構築のための内挿法

'spline' (既定値) | 'pchip'

包絡線構築のための内挿法。'Interpolation' と 'spline' または 'pchip' のいずれかで構成されるコンマ区切りのペアとして指定します。

以下のように Interpolation を指定します。

• x が滑らかな信号の場合は、'spline'

• x が滑らかでない信号の場合は、'pchip'

'spline' 内挿法は 3 次スプラインを使用します。一方で 'pchip' は区分的 3 次エルミート内挿多項式を使用します。

Display — コマンド ウィンドウの情報表示の切り替え

0 (既定値) | 1

コマンド ウィンドウの情報表示の切り替え。'Display' と、0 または 1 のいずれかで構成されるコンマ区切りのペアとして指定します。コマンド ウィンドウ内に生成されたテーブルは、生成された各 IMF のふるい分け反復の数、相対許容誤差、およびふるい分け停止基準を示します。テーブルを表示するには Display に 1 を、非表示にするには 0 を指定します。

出力引数

imf — 固有モード関数

行列 | timetable

固有モード関数 (IMF)。行列または timetable として返されます。各 IMF は振幅変調および周波数変調された信号で、包絡線は正でゆっくりと変化します。信号のスペクトル解析を実行するには、IMF にヒルベルト・ファン変換を適用します。hht および固有モード関数を参照してください。

imf は以下として返されます。

• x がベクトルの場合、各列が imf の行列

• x が単一データ列の timetable の場合、timetable

residual — 信号の残差

列ベクトル | 単一データ列 timetable

信号の残差。列ベクトルまたは単一データ列の timetable として返されます。residual は emd によって分解されていない元の信号 x の部分を表します。

residual は以下として返されます。

• x がベクトルの場合、列ベクトル

• x が単一データ列の timetable の場合、単一データ列の timetable

info — 診断の詳細

構造体

診断の詳細。以下のフィールドを含む構造体として返します。

• NumIMF — 抽出された IMF の数

  NumIMF は 1 ～ N のベクトルです。ここで N は IMF の数です。IMF が抽出されない場合、NumIMF は空です。

• NumExtrema — 各 IMF における極値の数

  NumExtrema は、長さが IMF の数に等しいベクトルです。NumExtrema の k 番目の要素は、k 番目の IMF にある極値の数です。IMF が抽出されない場合、NumExtrema は空です。

• NumZerocrossing — 各 IMF におけるゼロクロッシングの数

  各 IMF におけるゼロクロッシングの数。NumZerocrossing は、長さが IMF の数に等しいベクトルです。NumZerocrossing の k 番目の要素は、k 番目の IMF のゼロクロッシングの数です。IMF が抽出されない場合、NumZerocrossing は空です。

• NumSifting — 各 IMF の抽出に使用されたふるい分け反復の数

  NumSifting は、長さが IMF の数に等しいベクトルです。NumSifting の k 番目の要素は、k 番目の IMF の抽出で使用されたふるい分け反復の数です。IMF が抽出されない場合、NumSifting は空です。

• MeanEnvelopeEnergy — 各 IMF で取得された上側包絡線と下側包絡線の平均のエネルギー

  UE を上側包絡線、LE を下側包絡線とすると、MeanEnvelopeEnergy は mean(((LE+UL)/2).^2) です。MeanEnvelopeEnergy は、長さが IMF の数に等しいベクトルです。MeanEnvelopeEnergy の k 番目の要素は、k 番目の IMF の平均包絡線エネルギーです。IMF が抽出されない場合、MeanEnvelopeEnergy は空です。

• RelativeTolerance — 各 IMF に対する残差の最終相対許容誤差

  相対許容誤差は、前のふるい分けステップからの残差と現在のふるい分けステップからの残差の差分の 2 ノルムの二乗と、i 番目のふるい分けステップからの残差の 2 ノルムの二乗の比として定義されます。RelativeTolerance が SiftRelativeTolerance 未満の場合、ふるい分けプロセスは停止します。詳細については、ふるい分けの相対許容誤差を参照してください。RelativeTolerance は、長さが IMF の数に等しいベクトルです。RelativeTolerance の k 番目の要素は、k 番目の IMF で取得された最終相対許容誤差です。IMF が抽出されない場合、RelativeTolerance は空です。

詳細

経験的モード分解

経験的モード分解 (EMD) アルゴリズムは、反復処理で信号 x(t) を固有モード関数 (IMF) と残差に分解します。このアルゴリズムの中核コンポーネントでは、関数 x(t) の "ふるい分け" を行って、新しい関数 Y(t) を求めます。

• まず、x(t) の局所的最小値と局所的最大値を検索します。

• 次に、局所的極値を使用して、x(t) の下側包絡線 s₋(t) と上側包絡線 s₊(t) をそれぞれ構築します。包絡線の平均 m(t) を形成します。

• x(t) から平均を減算して、残差 Y(t) = x(t) − m(t) を求めます。

分解の概要は次のとおりです。

1. まず、r₀(t) = x(t) とします。ここで、x(t) は最初の信号です。i = 0 とします。

2. ふるい分けの前に、r_i(t) をチェックします。

   1. r_i(t) の局所的極値の総数 (TN) を求めます。

   2. r_i(t) のエネルギー比 (ER) を求めます (エネルギー比を参照)。

3. (ER > MaxEnergyRatio) または (TN < MaxNumExtrema) または (IMF の数 > MaxNumIMF) の場合、分解を停止します。

4. r_i,Prev(t) = r_i(t) とします。

5. r_i,Prev(t) のふるい分けを行って、r_i,Cur(t) を求めます。

6. r_i,Cur(t) をチェックします。

   1. r_i,Cur(t) の相対許容誤差 (RT) を求めます (ふるい分けの相対許容誤差を参照)。

   2. 現在のふるい分け反復回数 (IN) を取得します。

7. (RT < SiftRelativeTolerance) または (IN > SiftMaxIterations) の場合、ふるい分けを停止します。IMF の検索は完了し、IMF_i(t) = r_i,Cur(t) となります。そうでない場合、r_i,Prev(t) = r_i,Cur(t) とし、手順 5 に移動します。

8. r_i+1(t) = r_i(t) − r_i,Cur(t) とします。

9. i = i + 1 とします。手順 2 に戻ります。

詳細については、[1]および[3]を参照してください。

固有モード関数

EMD アルゴリズムは、反復ふるい分け処理により、信号 x(t) を IMF imf_i(t) と残差 r_N(t) に分解します。

$$X\left(t\right)={\displaystyle \sum _{i=1}^N{\text{IMF}}_i\left(t\right)+r_N\left(t\right)}$$

Huang et al. [1]により初めて導入されたとき、IMF は次の 2 つの特性をもつ関数であると定義されました。

• 局所的極値の数 (局所的最小値と局所的最大値の総数) とゼロクロッシングの数との違いが最大で 1。

• 局所的極値から構成された上側包絡線と下側包絡線の平均値が 0。

ただし、[4]に記載されているように、厳密な IMF が得られるまでふるい分けると、物理的な意味のない IMF になる場合があります。特に、ゼロクロッシングの数と局所的極値の数の違いが最大で 1 になるまでふるい分けると、純音のような IMF (つまり、フーリエ基底による投影で得られるものに非常によく似た関数) になる場合があります。これはまさに EMD が回避しようと努めている状態です。EMD では、物理的な意味を求めて AM-FM 変調されたコンポーネントを選択しています。

参考文献[4]では、物理的に有意な結果を得るためのオプションが推奨されています。関数 emd では、コーシー型停止基準 (ふるい分けの相対許容誤差) を使用することで、元の IMF 定義を緩和しています。関数 emd は、反復することで自然な AM-FM モードを抽出します。生成された IMF は、局所的極値-ゼロクロッシングの基準を満たさない場合があります。正弦波の固有モード関数のゼロクロッシングと極値を参照してください。

ふるい分けの相対許容誤差

"ふるい分けの相対許容誤差" は、[4]で推奨されているコーシー型停止基準です。現在の相対許容誤差が SiftRelativeTolerance 未満の場合にふるい分けが停止します。現在の相対許容誤差は、以下のように定義されます。

$$\text{Relative Tolerance}\triangleq \frac{{\Vert r_{\text{prev}}\left(t\right)-r_{\text{cur}}\left(t\right)\Vert }_2^2}{{\Vert r_{\text{prev}}\left(t\right)\Vert }_2^2}.$$

コーシー基準がゼロクロッシングと局所的極値の数を直接カウントしないため、分解によって返された IMF は固有モード関数の厳しい定義を満たさない可能性があります。この場合、既定値から SiftRelativeTolerance の値を減らすことを試すことができます。停止条件の詳細については、[4]を参照してください。参照では、経験的モード分解で厳密に定義された IMF を求める利点と欠点についても説明します。

エネルギー比

エネルギー比は、ふるい分けの開始における信号のエネルギーと平均包絡線エネルギーの比です[2]。現在のエネルギー比が MaxEnergyRatio より大きい場合に分解が停止します。i 番目の IMF に対して、エネルギー比は以下のように定義されます。

$$\text{Energy Ratio}\triangleq 10{\log }_{10}\left(\frac{{\Vert X\left(t\right)\Vert }_2}{{\Vert r_i\left(t\right)\Vert }_2}\right).$$

参照

[1] Huang, Norden E., Zheng Shen, Steven R. Long, Manli C. Wu, Hsing H. Shih, Quanan Zheng, Nai-Chyuan Yen, Chi Chao Tung, and Henry H. Liu. “The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis.” Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences 454, no. 1971 (March 8, 1998): 903–95. https://doi.org/10.1098/rspa.1998.0193.

[2] Rato, R.T., M.D. Ortigueira, and A.G. Batista. “On the HHT, Its Problems, and Some Solutions.” Mechanical Systems and Signal Processing 22, no. 6 (August 2008): 1374–94. https://doi.org/10.1016/j.ymssp.2007.11.028.

[3] Rilling, Gabriel, Patrick Flandrin, and Paulo Gonçalves. "On Empirical Mode Decomposition and Its Algorithms." IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing 2003. NSIP-03. Grado, Italy. 8–11.

[4] Wang, Gang, Xian-Yao Chen, Fang-Li Qiao, Zhaohua Wu, and Norden E. Huang. “On Intrinsic Mode Function.” Advances in Adaptive Data Analysis 02, no. 03 (July 2010): 277–93. https://doi.org/10.1142/S1793536910000549.

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

• コード生成では、timetable はサポートされていません。

• 'Interpolation' 名前と値のペアを使用して内挿法を指定する場合、コンパイル時の定数でなければなりません。

バージョン履歴

R2018a で導入

参考

アプリ

• 信号多重解像度アナライザー (Wavelet Toolbox)

関数

• hht | vmd

トピック

• 時間-周波数ギャラリー