解析信号とヒルベルト変換
関数 hilbert は、有限データ ブロックに正確に一致する解析信号を検出します。また、有限インパルス応答 (FIR) ヒルベルト変換フィルターを使用して解析信号を生成し、虚数部に対する近似を計算することもできます。
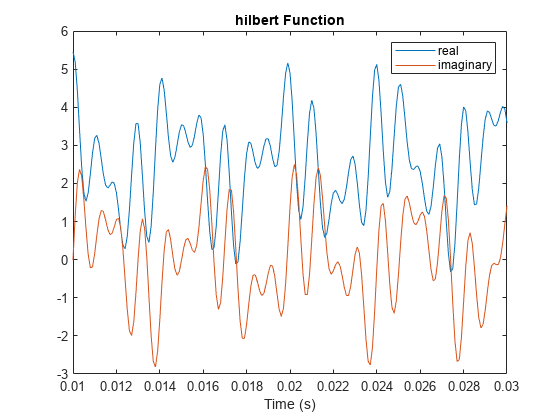
周波数が 203 Hz、721 Hz および 1001 Hz である 3 つの正弦波で構成されるシーケンスを生成します。シーケンスは 10 kHz で約 1 秒間サンプリングされています。関数 hilbert を使用して解析信号を計算します。これを 0.01 秒と 0.03 秒の間でプロットします。
fs = 1e4; t = 0:1/fs:1; x = 2.5 + cos(2*pi*203*t) + sin(2*pi*721*t) + cos(2*pi*1001*t); y = hilbert(x); plot(t,real(y),t,imag(y)) xlim([0.01 0.03]) legend("real","imaginary") title("Hilbert Function") xlabel("Time (s)")
元のシーケンスおよび解析信号のパワー スペクトル密度のウェルチ推定を計算します。ハミング ウィンドウを適用した長さ 256 のオーバーラップのないセクションにシーケンスを分割します。負の周波数では解析信号にパワーがないことを確認します。
pwelch([x;y].',256,0,[],fs,"centered") legend("Original","Hilbert")

関数 designfilt を使用して 60 次のヒルベルト変換器 FIR フィルターを設計します。400 Hz の遷移幅を指定します。フィルターの周波数応答を可視化します。
fo = 60; d = designfilt("hilbertfir",FilterOrder=fo, ... TransitionWidth=400,SampleRate=fs); freqz(d,1024,fs)

正弦波シーケンスをフィルター処理し、解析信号の虚数部を近似します。
hb = filter(d,x);
フィルターの群遅延 grd はフィルターの次数の 1/2 と等価です。この遅延を補正します。虚数部の最初の grd サンプルと実数部の最後の grd サンプルおよび時間ベクトルを削除します。0.01 秒と 0.03 秒の間の結果をプロットします。
grd = fo/2; y2 = x(1:end-grd) + 1j*hb(grd+1:end); t2 = t(1:end-grd); plot(t2,real(y2),t2,imag(y2)) xlim([0.01 0.03]) legend("real","imaginary") title("FIR Filter") xlabel("Time (s)")

近似の解析信号のパワー スペクトル密度 (PSD) を推定し、hilbert の結果と比較します。
pwelch([y;[y2 zeros(1,grd)]].',256,0,[],fs,"centered") legend("Hilbert","FIR Filter")
