このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

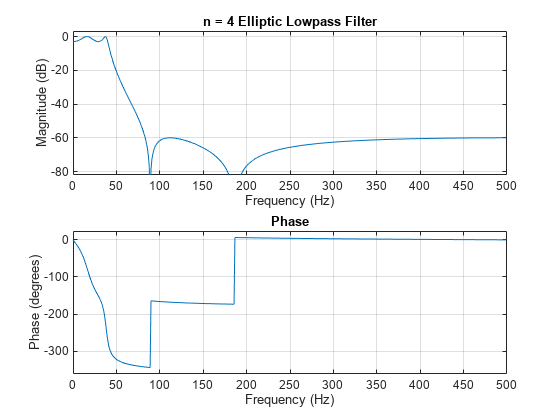
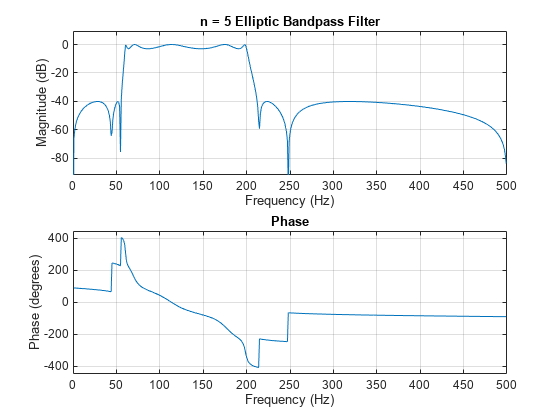
ellipord

楕円フィルターの最低次数

構文

[n,Wn] = ellipord(Wp,Ws,Rp,Rs)

[n,Wn] = ellipord(Wp,Ws,Rp,Rs,'s')

説明

[n,Wn] = ellipord(Wp,Ws,Rp,Rs) では、通過帯域リップルが Rp dB 以下で、阻止帯域で少なくとも Rs dB の減衰量をもつデジタル楕円フィルターの最小次数 n が返されます。Wp と Ws はそれぞれ、フィルターの通過帯域と阻止帯域のエッジ周波数で、0 ～ 1 に正規化されます。ここで、1 は π ラジアン/サンプルに相当します。また、対応するカットオフ周波数 Wn のスカラー (またはベクトル) も返されます。楕円フィルターを設計するには、出力引数 n と Wn を ellip の入力引数として使用します。

[n,Wn] = ellipord(Wp,Ws,Rp,Rs,'s') は、アナログ楕円フィルターの最小次数 n およびカットオフ周波数 Wn を求めます。1 秒あたりのラジアンを単位として周波数 Wp と Ws を指定します。通過帯域または阻止帯域を無限大にできます。

例

ローパス楕円フィルター次数

1,000 Hzのデータに対し、0 ～ 40 Hz で定義される通過帯域リップルが 3 dB 未満、150 Hz ～ナイキスト周波数 500 Hz で定義される阻止帯域リップルが少なくとも 60 dB のローパス フィルターを設計します。フィルターの次数とカットオフ周波数を求めます。

Wp = 40/500;
Ws = 150/500;
Rp = 3;
Rs = 60;
[n,Wp] = ellipord(Wp,Ws,Rp,Rs)

n = 4

Wp = 0.0800

2 次セクションとしてフィルターを指定し、周波数応答をプロットします。

[z,p,k] = ellip(n,Rp,Rs,Wp);
sos = zp2sos(z,p,k);
freqz(sos,512,1000)
title(sprintf('n = %d Elliptic Lowpass Filter',n))

バンドパス楕円フィルター次数

次に、60 ～ 200 Hz の通過帯域をもち、リップルが最大限でも 3 dB で、阻止帯域の減衰量が少なくとも 40 dBのバンドパス フィルターを設計します。サンプリング レートを 1 kHz に指定します。通過帯域の両側で阻止帯域の幅を 50 Hz にします。フィルターの次数とカットオフ周波数を求めます。

Wp = [60 200]/500;
Ws = [50 250]/500;
Rp = 3;
Rs = 40;

[n,Wp] = ellipord(Wp,Ws,Rp,Rs)

n = 5

Wp = 1×2

    0.1200    0.4000

2 次セクションとしてフィルターを指定し、周波数応答をプロットします。

[z,p,k] = ellip(n,Rp,Rs,Wp);
sos = zp2sos(z,p,k);

freqz(sos,512,1000)
title(sprintf('n = %d Elliptic Bandpass Filter',n))

入力引数

Wp — 通過帯域コーナー (カットオフ) 周波数

スカラー | 2 要素ベクトル

通過帯域コーナー (カットオフ) 周波数。0 ～ 1 の値をもつスカラーまたは 2 要素ベクトルとして指定されます。ここで、1 は正規化されたナイキスト周波数 π ラジアン/サンプルに対応します。

• Wp と Ws が両方ともスカラーで、Wp < Ws である場合は、ellipord はローパス フィルターの次数とカットオフ周波数を返します。フィルターの阻止帯域の範囲は Ws ～ 1、通過帯域の範囲は 0 ～ Wp です。

• Wp と Ws が両方ともスカラーで、Wp > Ws である場合は、ellipord はハイパス フィルターの次数とカットオフ周波数を返します。フィルターの阻止帯域の範囲は 0 ～ Ws、通過帯域の範囲は Wp ～ 1 です。

• Wp と Ws が両方ともベクトルで、Ws によって指定される区間に Wp によって指定される区間が含まれる場合は (Ws(1) < Wp(1) < Wp(2) < Ws(2))、ellipord はバンドパス フィルターの次数とカットオフ周波数を返します。フィルターの阻止帯域の範囲は 0 ～ Ws(1) および Ws(2) ～ 1 です。通過帯域の範囲は Wp(1) ～ Wp(2) です。

• Wp と Ws が両方ともベクトルで、Wp によって指定される区間に Ws によって指定される区間が含まれる場合は (Wp(1) < Ws(1) < Ws(2) < Wp(2))、ellipord はバンドストップ フィルターの次数とカットオフ周波数を返します。フィルターの阻止帯域の範囲は Ws(1) ～ Ws(2) です。通過帯域の範囲は 0 ～ Wp(1) かつ Wp(2) ～ 1 です。

データ型: single | double

メモ

フィルター仕様において、通過帯域/阻止帯域でのリップルが両側で等しくないバンドパス フィルター/バンドストップ フィルターが必要な場合は、ローパス フィルターとハイパス フィルターを別々に設計し、2 つのフィルターをカスケードに結合します。

Ws — 阻止帯域コーナー周波数

スカラー | 2 要素ベクトル

阻止帯域コーナー周波数。0 ～ 1 の値をもつスカラーまたは 2 要素ベクトルとして指定されます。ここで、1 は正規化されたナイキスト周波数 π ラジアン/サンプルに対応します。

データ型: single | double

Rp — 通過帯域リップル

スカラー

通過帯域リップル。スカラーとして dB 単位で指定します。

データ型: single | double

Rs — 阻止帯域の減衰量

スカラー

阻止帯域の減衰量。スカラーとして dB 単位で指定します。

データ型: single | double

出力引数

n — 最小フィルター次数

整数スカラー

最小フィルター次数。整数スカラーとして返されます。

Wn — カットオフ周波数

スカラー | ベクトル

カットオフ周波数。スカラーまたはベクトルとして返されます。

アルゴリズム

ellipord では、参考文献 [1] に記載されている楕円ローパス フィルターの次数予測式が使用されます。この関数は、アナログとデジタルのいずれの場合もアナログ領域で処理を行います。デジタルの場合には、周波数パラメーターが s 領域に変換され、次数と固有振動数が推定され、その後 z 領域への逆変換が行われます。

ellipord では、まず希望するフィルターの通過帯域周波数を 1 rad/s (ローパス フィルターおよびハイパス フィルターの場合)、または -1 および 1 rad/s (バンドパス フィルターおよびバンドストップ フィルターの場合) に変換することにより、ローパス フィルターのプロトタイプが作成されます。次に、阻止帯域仕様を満たすローパス フィルターに必要な最小次数が計算されます。

参照

[1] Rabiner, Lawrence R., and B. Gold. Theory and Application of Digital Signal Processing. Englewood Cliffs, NJ: Prentice Hall, 1975.

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

すべての入力は定数でなければなりません。式や変数は、その値が変化しない限りは使用できます。

バージョン履歴

R2006a より前に導入

参考

buttord | cheb1ord | cheb2ord | ellip